NOIP 1998 普及组算法题解

零、背景

之前已经分享了 1997 年算法比赛题解，地址如下：《NOIP 普及组》和《NOIP 提高组》、《NOI day1》、《NOI day2》。

今天分享一下 1998 年 NOIP 普及组题解。

PS：题解代码已上传至网盘，公众号回复 NOIP-1998 获取。

一、三连击

题意：将 1~9 这 9 个数字分成三组，每组都是一个三位数，且这三个三位数的比例为 1:2:3。
输出所有满足条件的三位数。

思路：枚举

枚举第一个三位数，然后根据比例计算出后两个数字，判断是否满足要求。
复杂度：O(10^3)。

二、阶乘之和

题意：计算 S=1!+2!+3!+⋯+n!。

思路：高精度计算

最暴力的做法是封装高精度类，然后依次计算阶乘，最后求和。

观察阶乘和，存在大量重复计算，故可以提取公共因子，减少计算量。

  1!+2!+3!+⋯+n!
= 1 * (1 + 2!/1! + ... + n!/1!)
= 1 * (1 + 2 * (1 + 3!/2! + ... + n!/2!)
= ...
= 1 * (1 + 2 * (1 + 3 * (... + (n-1) * (1 + n))))   

这样就可以把阶乘和转化为：乘以一个数字，再加上 1。

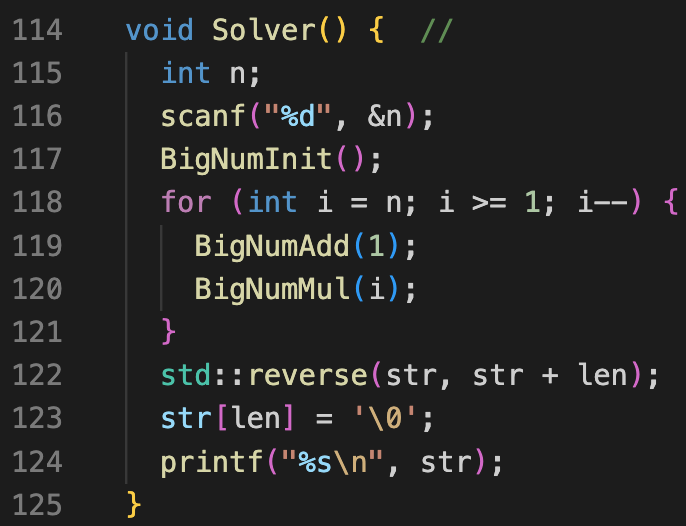
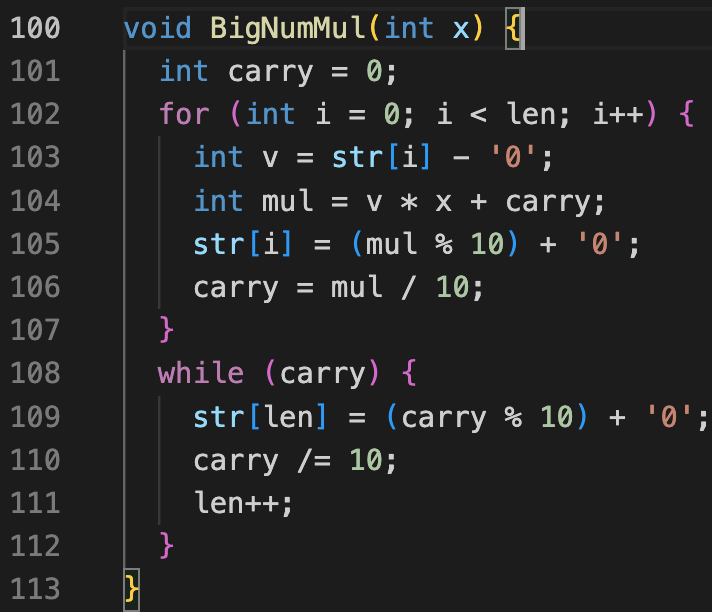
只需要实现高精度“乘以一个数字”以及“加上 1”，代码就简单多了。

三、幂次方

题意：给一个正整数，需要使用 2 的幂次方来表示。
幂次方的指数也可能是一个大于 2 的数字，需要递归地使用 2 的幂次方来表示。

思路：递归

输入范围不超过 2 万，可以发现幂次方的指数不超过 16，故可以先预处理出 16 以内所有整数对应的 2 的幂次方表示。

然后对于输入的数字，先分解出第一层 2 的幂次方，直接查表拼装答案即可。

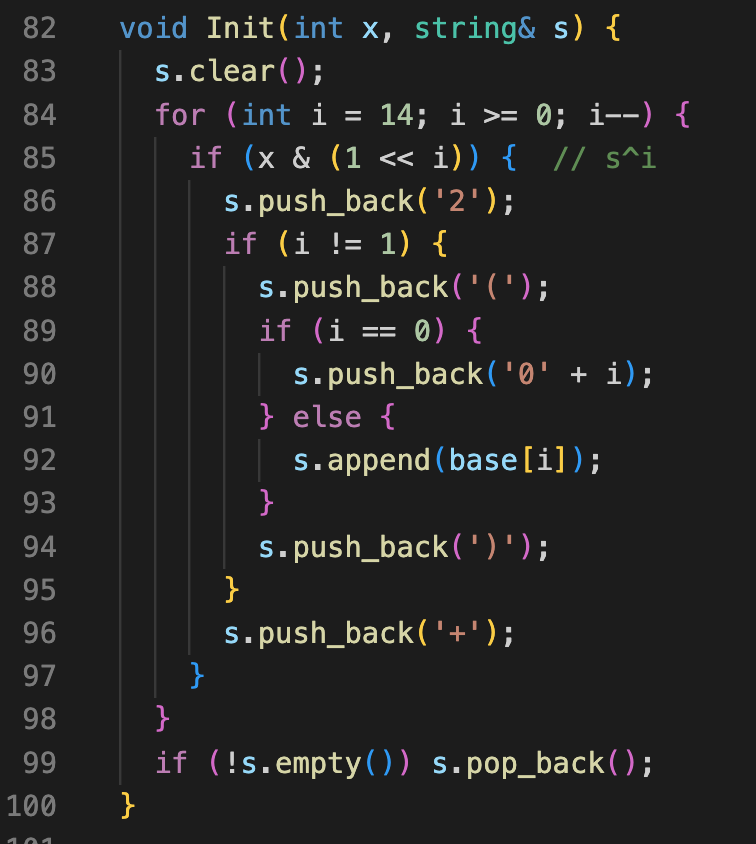
注意事项：2^1 需要使用 2 来表示。

四、最后

这次比赛比较简单，考察了枚举、高精度、模拟三类基础算法。

《完》

-EOF-

本文公众号：天空的代码世界

个人微信号：tiankonguse

公众号ID：tiankonguse-code