NOIP 1998 提高组算法题解

零、背景

之前已经分享了 1998 年 NOIP 普及组题解，见《NOIP 普及组》。
这里继续整理 1998 年 NOIP 提高组题解。

一、车站

题意：火车在始发站车上有 a 人。
第二站上车人数与下车人数相同。
从第三站起，每一站的上车人数等于前两站上车人数之和，下车人数等于上一站上车人数，一直到终点站的前一站。
最后第 n 站时，车上剩余 m 人全部下车。
问从第 x 站开出时，车上有多少人。

思路：模拟。

第一站上车 a 人，设第二站上车 b 人，则每一站的上车人数、下车人数、以及开出后的车上人数都可以写成 a*X + b*Y 的形式。
根据递推关系，可以把终点站开出前的车上人数表示为 m = a*X + b*Y，从而解出 b。
再从第一站开始按规则模拟一遍，即可得到第 x 站开出时的车上人数。

二、进制位

题意：给出一个“未知进制”的加法表，表中的数字全部用字母表示。
问是否存在某个合法的进制，以及一组字母到数字的映射，使得整个加法表成立。

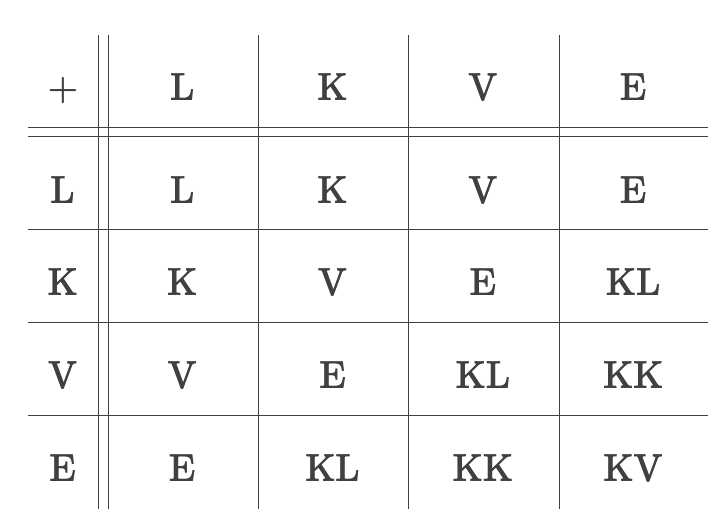
思路：贪心（从确定的信息入手逐步还原映射）。

结论：加法表有几行（也有几列），进制就是几进制。

结论：有几行肯定就是几进制。

证明：由于进位的存在，两个个位相加十位只能是 1，故字母中肯定存在 1。
1 加 1 肯定可以得到 2。
由此递推，在进位之前，所有数字都会存在。
最大的数字再进位，各位是0，故 0 也必须存在。

三、拼数

题意：给 n 个非负整数，把它们首尾相连拼成一个尽可能大的数。

思路：搜索或贪心。

最容易想到的是搜索。

暴力枚举所有组合，复杂度 O(n!)。
得分： 38 分。

剪枝1：如果已经得到一个答案，当前搜索的前缀就可以与答案比较，看是否必然不是最优答案。

剪枝2：枚举所有组合时，一般是 mask 来标记是否已枚举。
如果使用枚举的数字与数组最后一个数字交换，则可以少遍历几次。

剪枝3：对数字按字典序排序，有效从大到小枚举。

得分：100分。

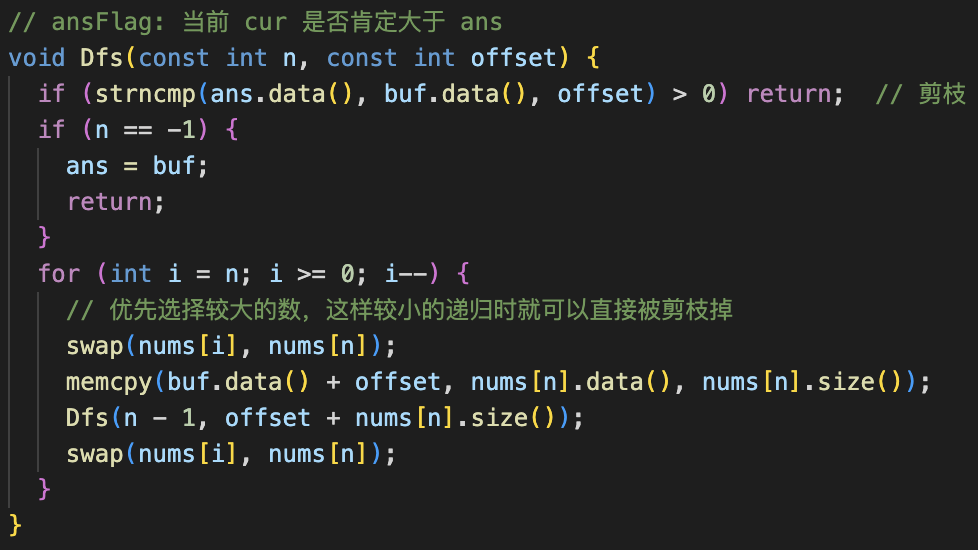
其实，这个题也可以用贪心来解。

显然，位数越低，数字越大越好。
所以第一个数字肯定选择字典序最大的数字。

但是存在一种特殊的情况。
例如最大的数字是 991，而还有一个数字 9，选择 9 可以得到更优的答案。

那对于两个数字，到底先选择谁更优呢？
假设其他数字位置都固定，只有两个数字可以交换，显然，这两个数字哪个在前面与哪个在后面，最优答案是确定的。

基于此，我们可以把所有排列组合都当做一个点，只有两个数字交换的情况，可以看做是两个点之间的边。
可以发现，这个图是诺拓扑有序的。

所以，一种贪心方法是不断的选择两个数字，判断交换后是否可以得到更优的答案。
复杂度：O(n^2)

其实，可以发现，上面的过程其实就是一种排序的过程。
而且可以在图中找到一个只交换相邻数字的路径。
故，可以只对相邻的数字不断的进行判断与交换即可。

这个过程既然就排序，那么，我们也可以对所有数字按字典序进行排序，然后从大到小进行拼接即可。
复杂度：O(n log(n))

四、最后

这次比赛其实有点难。

第二题加法表，不容易想到有几行就是几进制。
第三题贪心这个思路也是不容易想到的，而搜索写的不好，很容易超时。

所以，我感觉这次比赛出的不好，都需要贪心才能写出正解，非贪心的话只能搜索得到部分分了。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code