算法中的木桶短板理论

大家好，这里是tiankonguse的公众号(tiankonguse-code)。
tiankonguse曾是一名ACMer，现在是鹅厂视频部门的后台开发。
这里主要记录算法，数学，计算机技术等好玩的东西。

这篇文章从公众号tiankonguse-code自动同步过来。
如果转载请加上署名：公众号tiankonguse-code，并附上公众号二维码，谢谢。

零、背景

最近几周事情比较多，写技术文章的时间少了，不过还是可以抽点时间写几道算法题的。
于是就计划着每天抽十几分中做几道leetcode算法题，然后把题的分析分享给大家。
昨天刷了积水相关的问题，当我分析完对应的方法后，发现方法竟然是木桶短板理论。
所以这里分享给大家。

一、题意

有两道对应的题， 一个是二维的，一个是三维的。

二维： Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

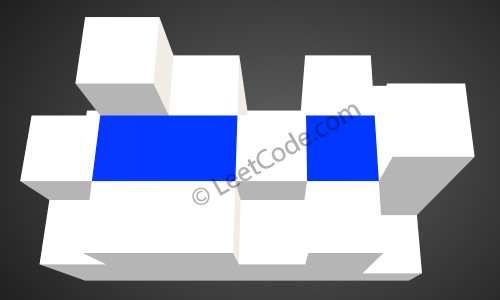
三维： Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.

题意可以理解为有一些柱子，二维是柱子排成一排，三维是柱子放在一个矩形平面上.
如图所示，中间凹槽可以积水，求积水量。

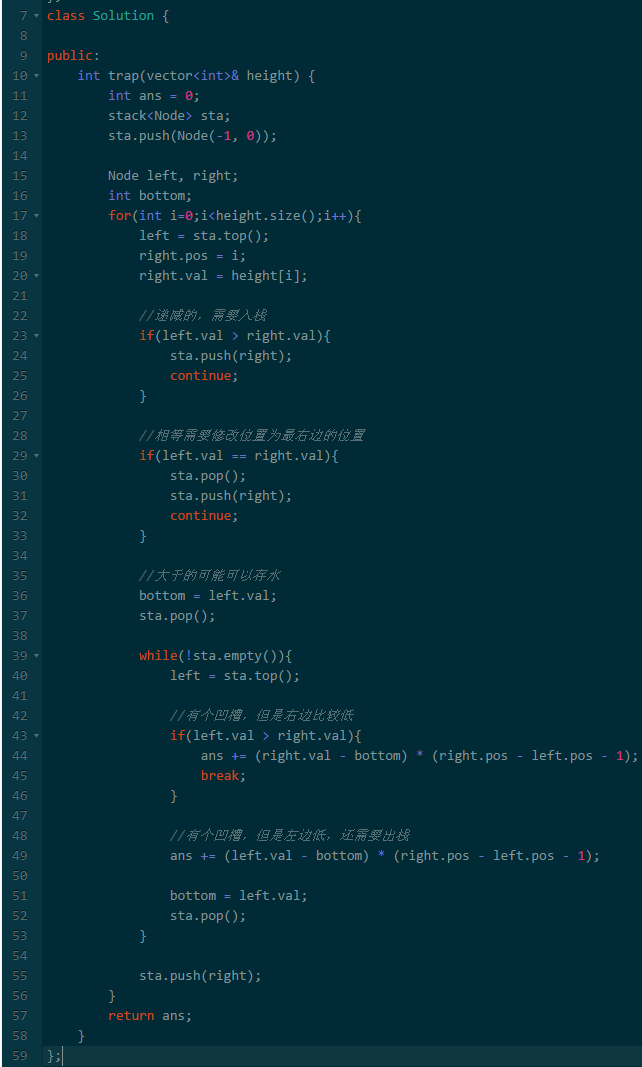
二、二维问题分析

二维的话很容易想到一些暴力的方法，但是复杂度比较高。

第一种暴力思路是从左到有依次判断每个位置可以积多少水。
那怎样判断一个位置能积多少水呢？求出这个位置左边和右边的最大值以及位置，然后就可以算出来了。
复杂度是O(n^2).

第二种暴力是判断从下到上每个高度可以储存多少水。
对于每个高度，从左到有扫描，低于这个高度的位置标记为0，大于等于这个位置的标记为1. 然后判断1之间的0的个数即可。
复杂度是O(n * maxHeight)

其实想象一下积水的特征，可以发现是两边高中间低的。
根据这个特征，我们可以得出下面几个结论：

在最左边，如果第二个高度高于第一个高度，则第一个高度肯定对总结果没有影响的。
换句话说，从左到右只有递减的高度才有可能存在积水。

于是我们可以维护一个递减的堆栈。
遇到非递减时，说明可以储存一部分水了，然后更新堆栈。

复杂度O(n).

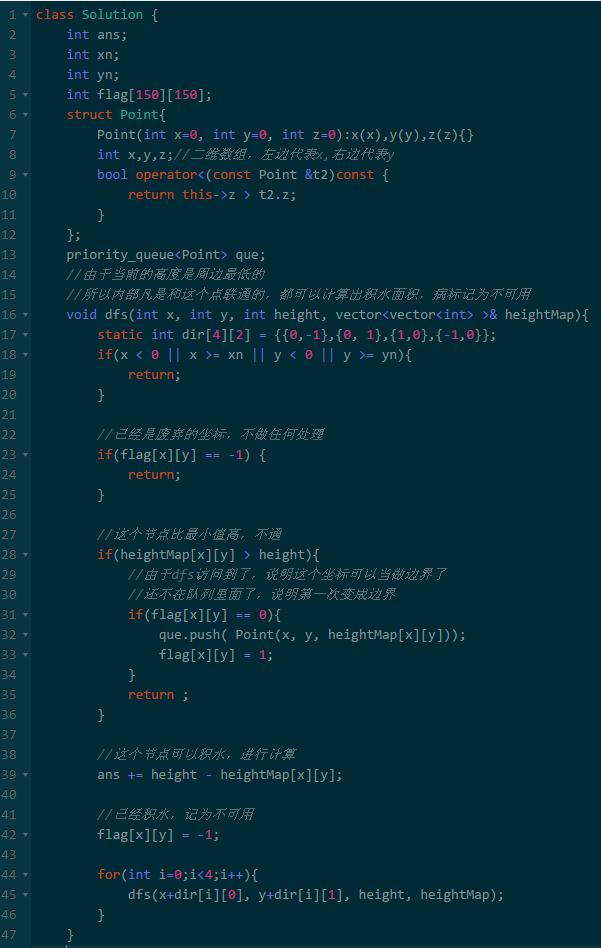
三、三维问题分析

这个三维积水问题其实和二维很类似。
二维的时候给了两个暴力方案和一个最优方案。

这里n和m上限是200, 高度上限是20000， 暴力的话复杂度就有点高了。

所以我们需要想其他办法了。
看看二维的最优思路，特点是维护一个递减的堆栈，遇到更高的点时，就存在积水。
转化一下就是当两边高中间低时才有积水。

对于三维，是四个方向，也就是四边高中间低的时候才有积水。
所以我们可以根据木桶原理，找到最低的那个边，然后就可以知道可以存多少水了。
木桶原理：一只木桶盛水的多少，并不取决于桶壁上最高的那块木块，而恰恰取决于桶壁上最短的那块。

对于积水的坐标找到后，积水区域其实就变成了木桶的边界了。
所以我们不断的寻找最低的木桶边界，然后计算积水，就可以得到所有积水了。

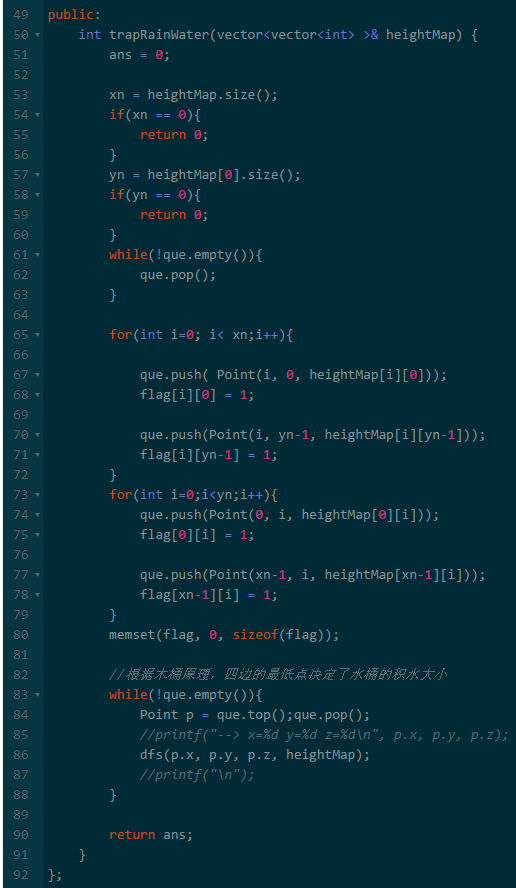
上一段话比较抽象，大家可以这样来做一个思维实验。
假设这个三维物体就是有一根根底面积是1 * 1的木板做的桶。
起初木桶周围水的高度是0，然后水慢慢的升高。 则第一个被水淹没的肯定是周围与水接触的木板，而且这个木板还是最矮的那个。

假设水的高度继续升高，则水就可以顺着这根最短的木板流到水桶的内部。
能够流入的水量全是内部相连，且高度低于这个最低木板的高度。

假设内部相通的地方已经被水填充并且和最低木板的高度一样了。
水平面继续升高，此时那些已经填充水的木板上面的水不能计算为积水，因为是和外面想通的，水平面降下去后这些水还是会流跑的。
水平面继续升高，下一个可以流入水的木板肯定是和水相连的最低的木板。

如果我们可以维护一个和水相连木板的数据结构，并可以快速找到最低的木板，然后计算因为这个短板新增的积水量。

复杂度：O(n*m)

四、二维上的木桶原理

我们使用木桶原理解决了三维积水问题，现在回过头来发现二维也可以使用这个原理在O(n)的复杂度解决问题。

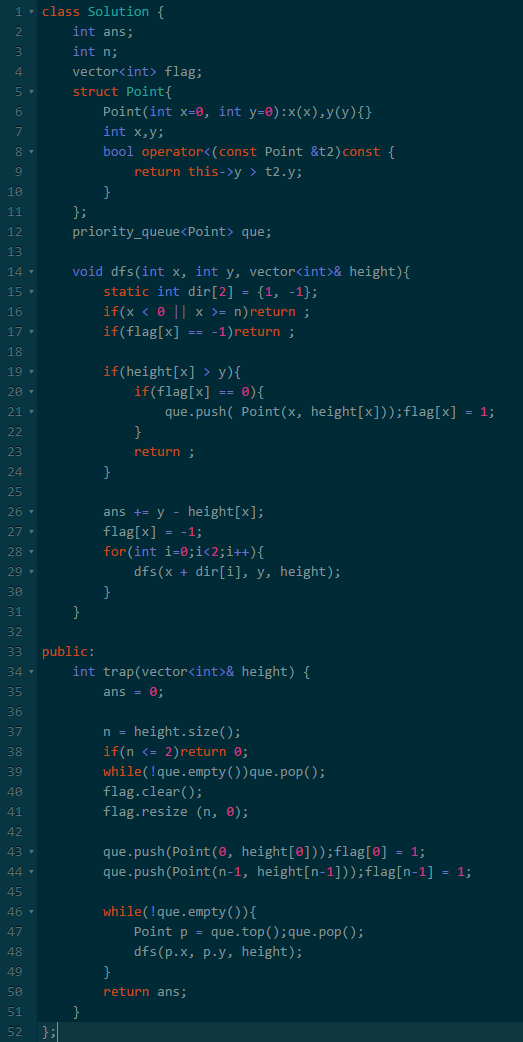
八、总结

对于这些题，然后还有其他的方法，关键在于我们如何思考这些题。
使用木桶原理的话，二维和三维就是同一类型的题，套公式即可解决了。

对了现在开通了公众号和小密圈。
博客记录所有内容。
技术含量最高的文章放在公众号发布。
比较好玩的算法放在小密圈发布。
欢迎大家加入看各种算法的思路。

长按图片关注公众号，阅读不一样的技术文章。