【算法】Leecode 第88场比赛回顾

一、背景

我大概是 2015 年听说的 Leecode 的，然后开始刷题，刷了一大部分，所有题都提交到 github 上了。
地址在这里（点击底部原文可以点击链接）： https://github.com/tiankonguse/leetcode-solutions

转眼间，已经过了四年了。
leecode 上的题也翻了好几倍了。
今年开始继续维护这个 github 项目，把其他题也做了，补上来。

今天做了第88场比赛，有四道题，下面分别来看看吧。

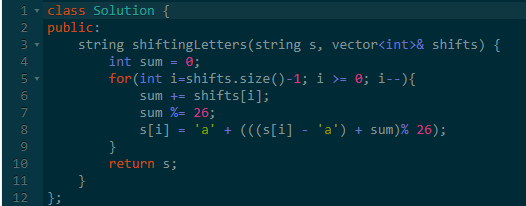
二、循环移动字符串

对于字符串的循环移动，大家应该都听说过。
对于字母表有26个，循环移动一次，a 将会变成 b，b 将会变成 c，依次递推下去，最后的 z 将会变成 a 。
如果循环移动 n 次，就是重复上面的操作 n 次。

如果仅仅是这样，那就太简单了。
所以题意稍微加强了一些：对于长度为 len 的字符串，有 len 次操作， 每次操作都是对前 i 个字符循环右移 shifts[i] 次。

面对这个加强的题意，如果我们单独看每个字符的话，就会发现，题意是对每个位置的字符循环移动了多批，每批移动若干次。
所以我们可以统计出每个字符移动的次数，然后进行移动转化即可。

这里面有个注意点是：题意要求每次操作对前i个字符循环移动，如果我们从前到后分别计算移动次数，复杂度就是O(n^2)了。
而我们从后到前的话，就可以累积加了，这样复杂度就是O(n)了。

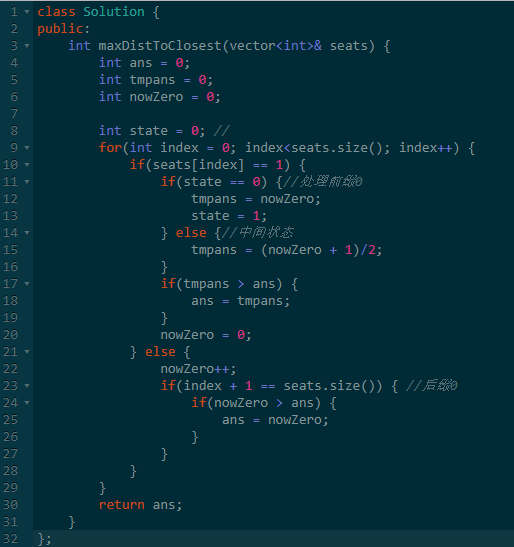
三、离自己距离最近的最大距离

这道题的意思是有n位置，有些位置有人坐，有些位置没人坐，求我们挑一个位置，使得离理解距离最近的那个人的距离最大。

面对这个题意，我们需要分三种情况：坐最前面，坐最后面，坐中间。
坐最前面和最后面时，空位置的个数就是距离，而坐中间时，由于左边和右边都有人，最大距离就是最大空位置的二分之一了。

当然，有一些边界情况，比如没有最前面、没有最后面、没有中间等。
考虑着三种情况后基本上就没什么问题了。

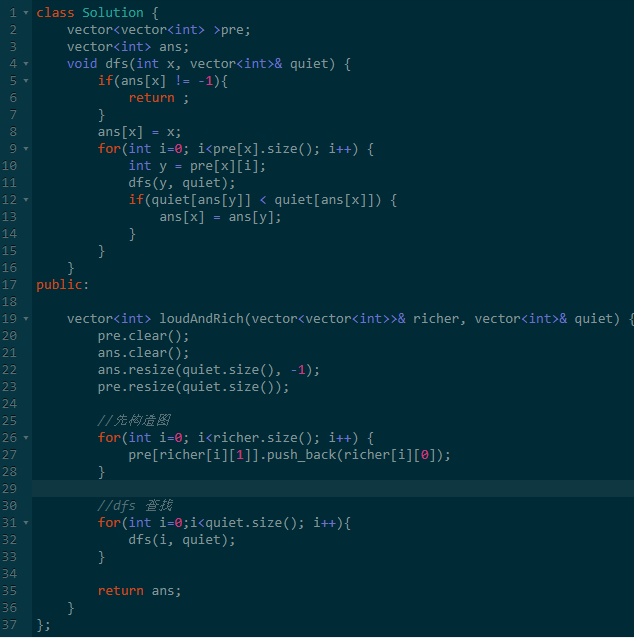
四、比自己富但是最安静的人

这道题算是图论题了。
给一个无环有向图，代表两个人谁比谁富有。
每个有有一个不同的安静值，求所有人的比自己富有但最安静的那个人。

对于这道题，如果我们把这个有向图画出来，并手动在图上计算出每个人的答案，我们大概就知道怎么做这道题了。

对于每个人，我们只需要计算 所有比这个人直接富有的人的安静值答案，取最小值即可。
这里的直接富有代表两个人之间有条边。

如果这样暴力做的话，复杂度是O(n^2)。
观察发现，很多人的最优安静值我们重复计算了，所以做一个标记，算过的不再算了，这样复杂度就是O(n)了。

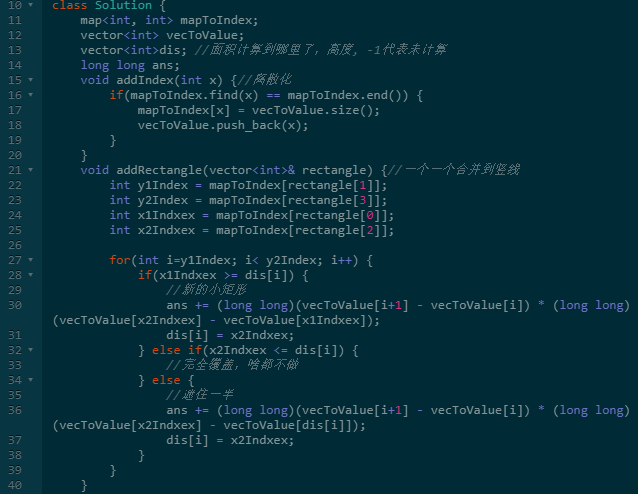
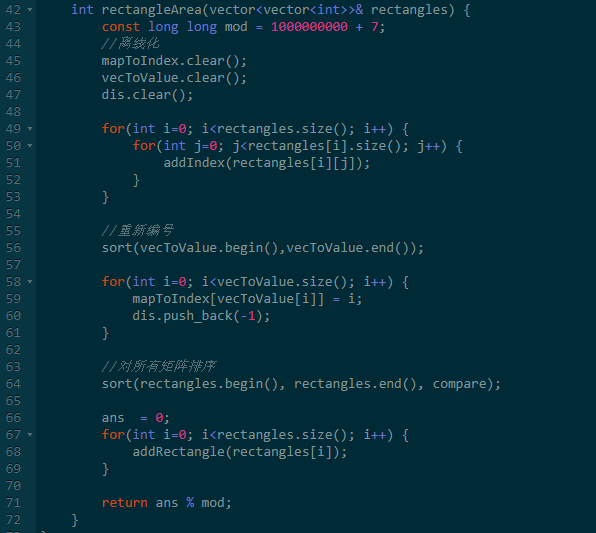
五、矩阵面积并集

这道题含义很简单，给一堆矩形，求面积的并集。
并集意味着这些矩形会相互覆盖，考虑到四个点坐标系的复杂性，两个矩形的关系有很多很多种情况。

所以我们需要换个思路来看这个问题了。

第一种思路是一个个扫描矩形，每当矩形相交时，我们就把矩形拆分成互相不相交的小矩形。
但是考虑到极端情况，我们可能拆分出f(n) = f(n-1) + k*n = O(n^2)的小矩形来，而由于是边拆分边比较，时间复杂度就是O(n^3)了。
当然，对于这道题，这个复杂度可以过，但是实现还是相当复杂的，尤其是拆分矩形的逻辑，分的情况还是蛮多的。

而另一个思路是扫面法。
比如说我们有一个垂直于x坐标轴的一根竖线，开始的时候在负无穷。
然后我们开始向正方向移动，每遇到一个矩形，我们就加上这个矩形的面积（只加新增的部分）。
这个可以理解为高级版的俄罗斯方块，每次下落的时候不是完全的挨着，而是可以部分重叠。
这个重叠部分就是和之前累积矩阵的交集。

这是再看我们的竖线，发现有特征了：不同的高度，可能向左累积了不同的长度矩形。
所以我们需要记录每个位置向左累积的长度。
这里唯一的问题是点太多，无法表示所有的点。

面对矩形的数值范围比较大，我们发现矩形个数比较少，我们可以不记录点，而记录线段。线段的端点就是矩形的Y坐标。
为了方便表示，我们需要提前计算出所有的线段，并储存在数组中，这个过程我们称为坐标离散化（不同坐标进行编号）。
离散化后，我们就可以就可以只记录编号了，一个编号代表一个区间，这样就可以表示整根竖线向左突出的距离了。

六、最后

这四道题整体还算简单，有字符串、计算、图论、几何四种题型，大家可以练习一下。
由于我好久没做 Leecode 了，做最后一题时，提交怎么都编译不过，浪费不少时间。 接下来就是搭建环境了，有了顺畅的环境，开发、编译、测试就可以一气呵成了。

目前我的环境大概如下，后续会加一个 DIFF 的功能，返回 YES 或 NO 来快速判断样例是否通过。

-EOF-