【算法】二维数组就是这么简单

一、背景

这篇文章主要通过几个具体的例子来看怎么使用二维数组。

二、二维数组

二维数组和一维数组一样，也是有一系列元素组成。
但是二维数组的元素排列在矩形网格里，而不是一条直线。

当然，有些语言里面，二维数组是通过一维数组实现的，而在其他一些语言中，则不存在二维数组的概念。

例如在C/C++中，二维数组底层储存为一维数组。
下图显示了大小为 M * N 的数组 A 的实际结构：

因此，如果我们将 A 定义为也包含 M * N 个元素的一维数组，那么实际上 A[i][j] 就等于 A[i * N + j]。

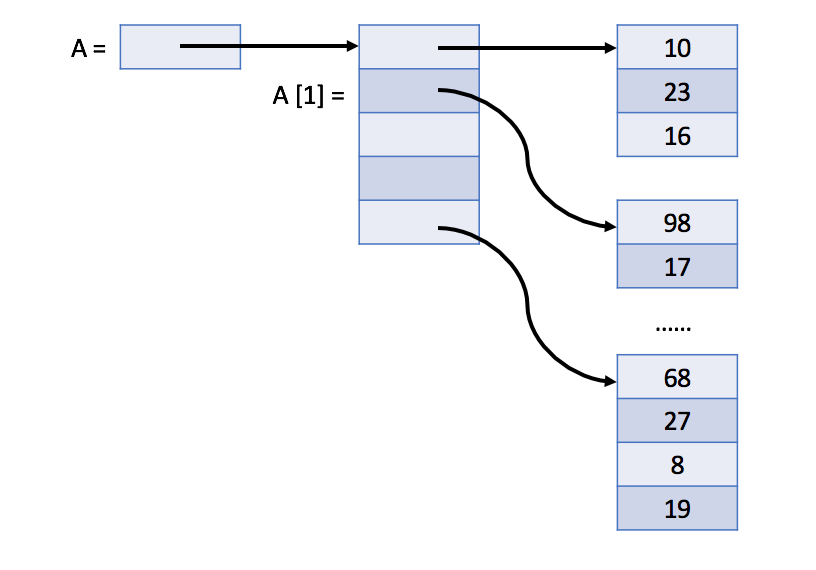
而在Java中，二维数组其实就是包含M个元素为一维数组，而每个元素又是一个大小为N的一维数组。
下图显示了 Java 中二维数组 A 的实际结构：

而对于动态二维数组，则是一维动态数组的元素还是一维动态数组。

具体可以看下面的题吧。

三、对角线遍历

告诉你一个N * M的二维数组，求按对角线遍历这个二维数组，并输出遍历的元素。
遍历规则可以参考下图。

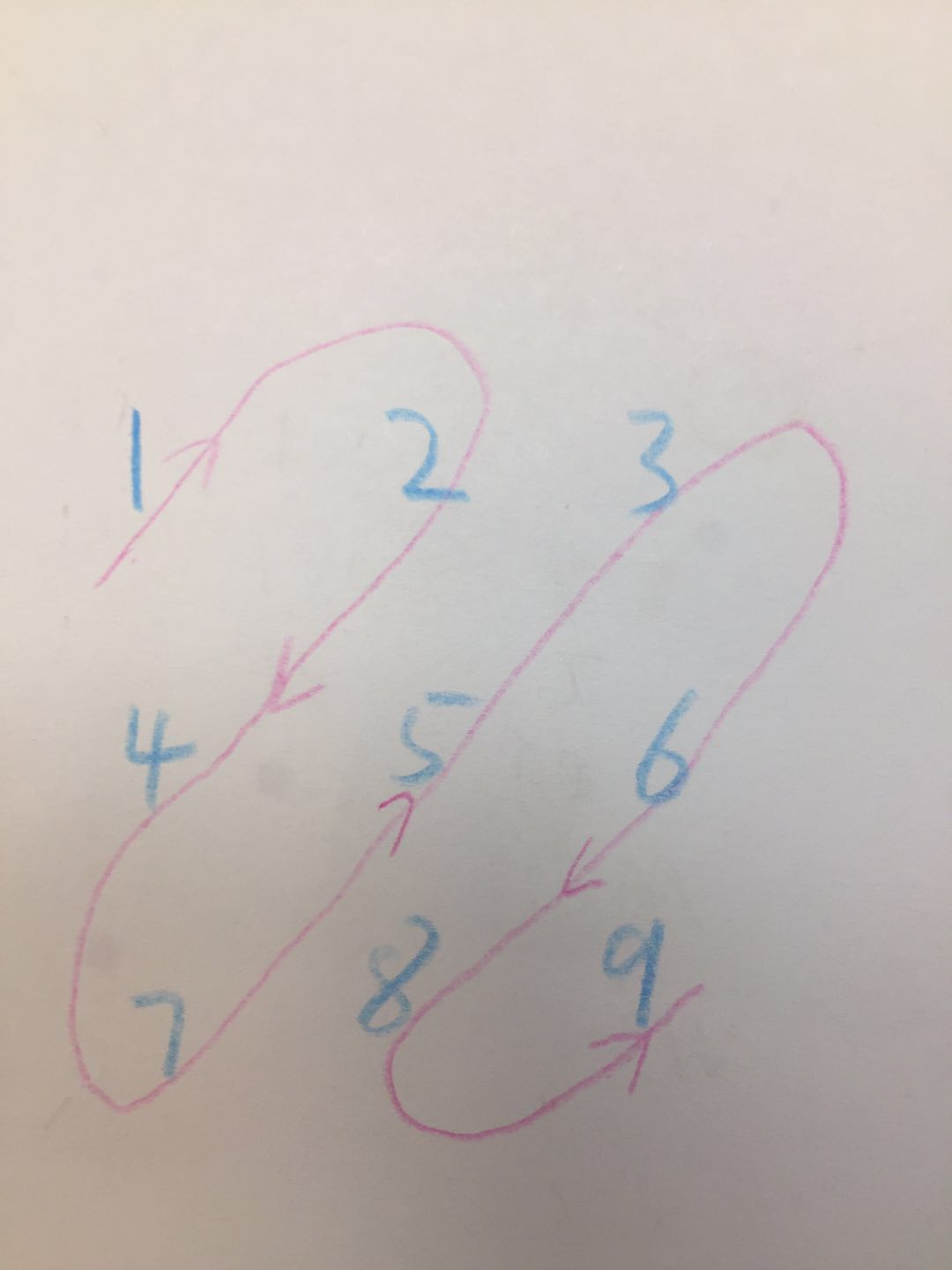
其实这道题看着很简单，但是做起来会发现很复杂，需要考虑的情况太多。
一会是对角线向上，一会是对角线向下。
一会是左边越界，一会是右边越界，或者上边越界，或者下边越界。

所以我们需要对这道题进行划分，来减少边界的判断。

简单看下上图，可以发现答案是沿着对角线以S型的方式走一遍。
所以我们可以分三步走。
第一步得到所有的对角线。
第二步判断对角线是否需要翻（S型）。
第三步将对角线拼接到答案上。

第一步，我们可以以对角线最上面的顶点的行坐标来划分。
分两部分：第一部分行坐标是矩阵的最上边0，从左到右。第二部分行坐标是矩阵的最右边，从上到下。
有了最上面顶点的坐标，我们就可以循环斜着扫描，每扫描下一行，列数依次减一，只要没越界，都属于这个对角线上的合法坐标。

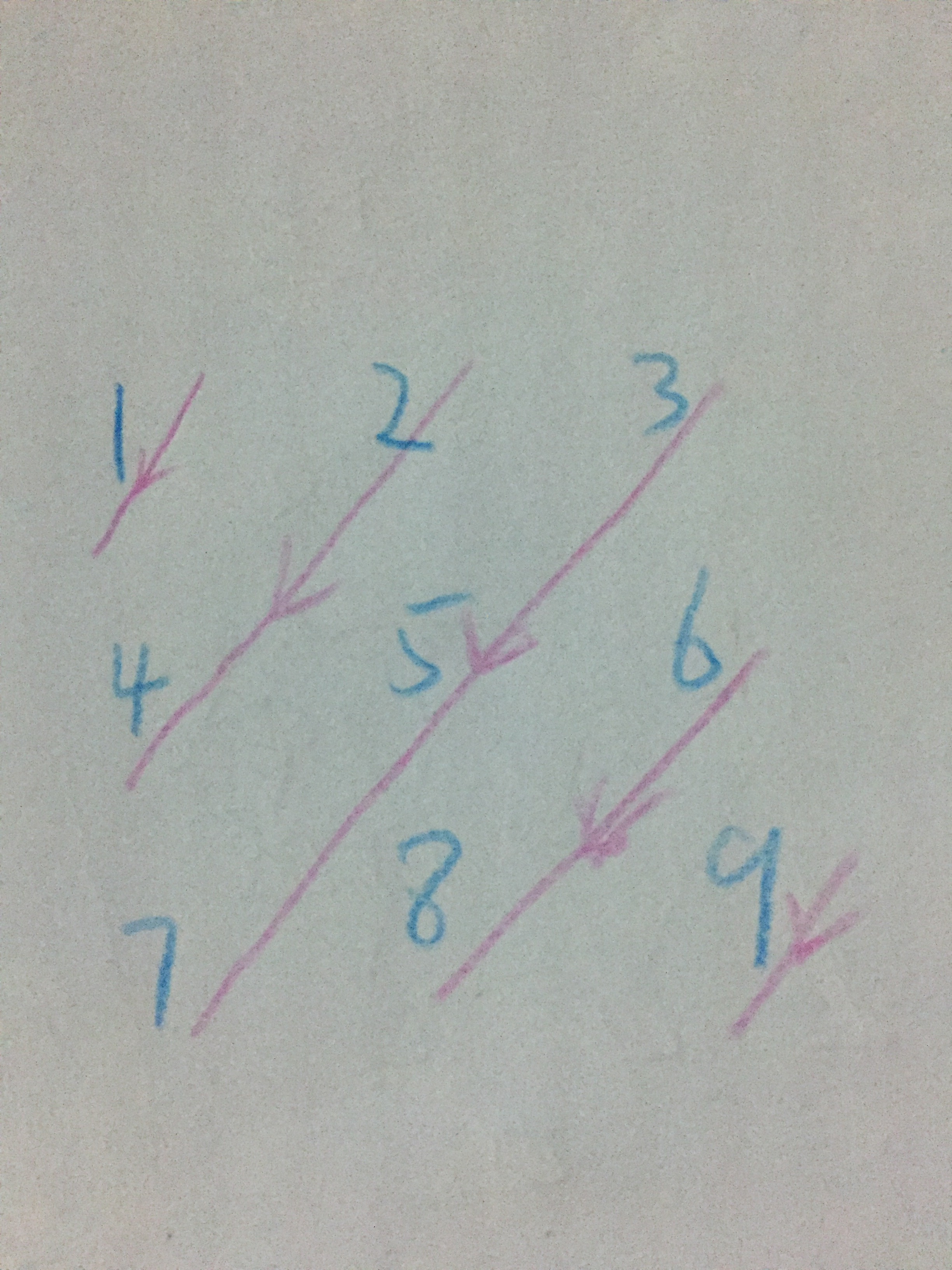
第二步，可以发现对角线的方向按奇偶性在翻转，所以我们使用一个flag来标记即可。
第三步就是将对角线的数据拼接到答案上，循环拼接即可。

四、螺旋矩阵

给一个N * M的矩阵，按顺时针输出所有元素。

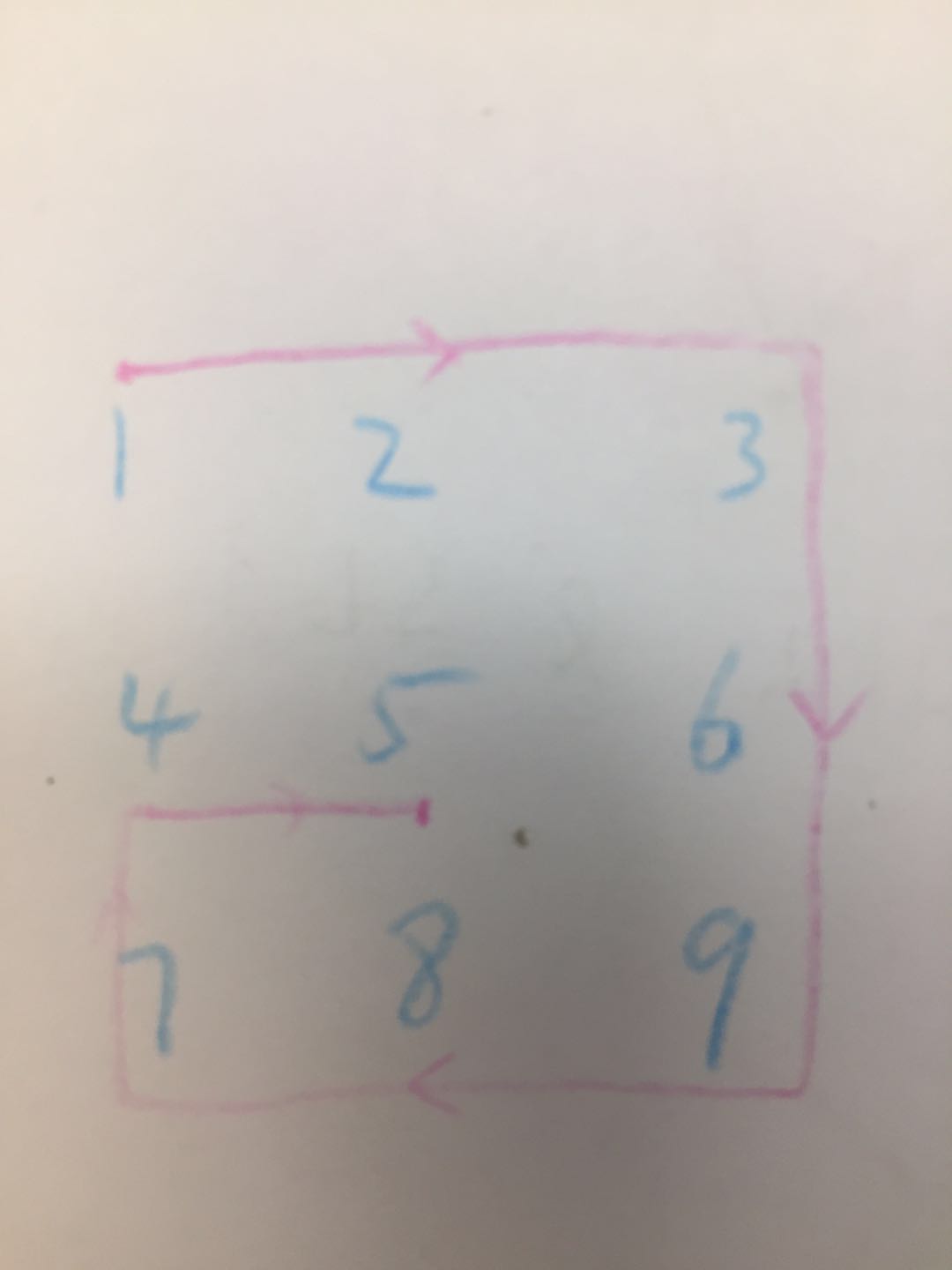
上面那道题对角线是两个方向，现在螺旋遍历则是四个方向了。
此时需要考虑的特殊情况更多了。

我们逐一写出所有方向的逻辑也可以，但是很容易漏写。

面对矩阵的这种问题，常用的方法是模板化。
具体来说就是将所有操作进行抽象提取，划分为不同的状态，每个状态有自己的模板操作。
模板化后的好处是我们可以直接循环就可以完成遍历矩阵了。

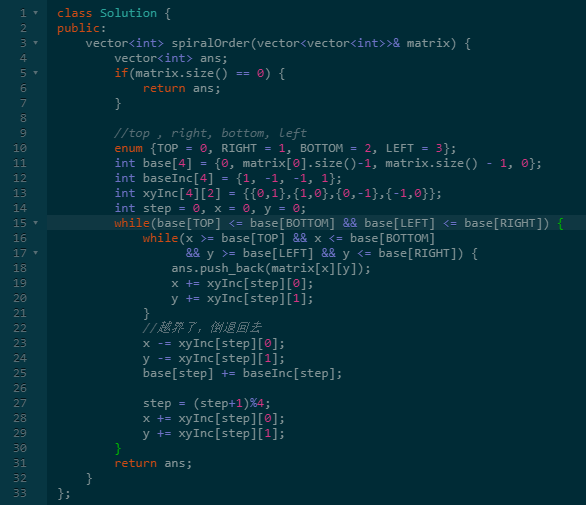
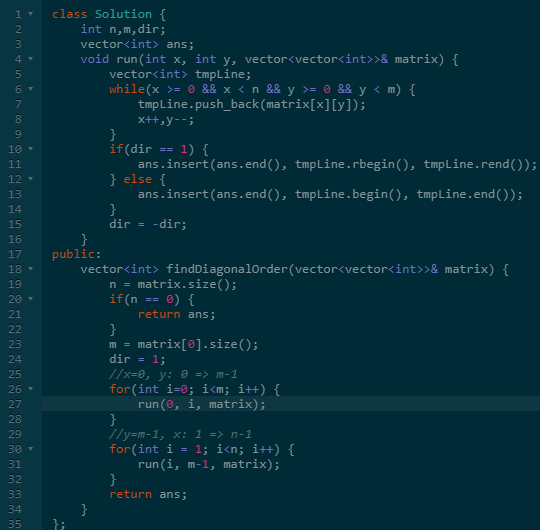
比如上面这个代码。
第一个是将操作按顺时针标号模板化，这样的好处是我们可以通过运算得到下一个操作。
第二个是将上下左右的边界base进行模板化，同时储存一个维护边界的辅助数组baseInc。
第三个是将最关键的矩阵遍历计算规则xyInc模板化。

通过上面三个模板化，我们就可以快速判断当前是不是处理完了（最外层循环）。
也可以快速判断当前方向的遍历是否完成了（内层循环）。
当我们遍历完一个方向后，x,y肯定是越界的，所以需要回滚，并转换到下个方向状态。
又由于回滚后的坐标之前已经处理，所以需要在新的方向移动一下，到达新的未处理的位置。

就这样，一道很复杂的螺旋遍历矩阵问题，就转化为了两层循环的问题了。

五、杨辉三角

输入一个数字N，输出高度为N的杨辉三角。
注：杨辉三角参考下图。

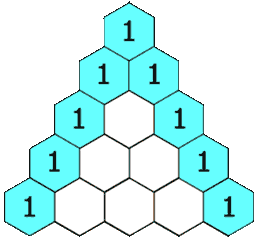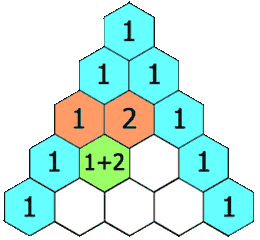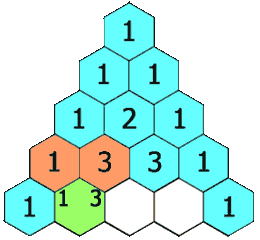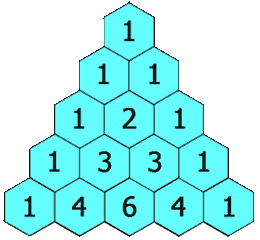
这道题与前面两道题相比就简单多了。

根据动图中的效果，我们可以发现一个规律：下一行某个位置的值时上一行相同位置和前一个位置值的和。
即f(x, y) = f(x-1, y) + f(x-1, y-1)。
而对于每一行的第一个和最后一个，不满足上面的规律（越界了），但值都是1，特殊处理即可。
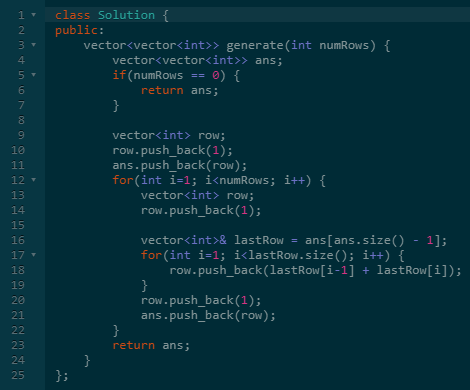
于是我们就可以按照这个规律写出答案了。

七、最后

在二维数组里面，对角线遍历和螺旋遍历就有点技术含量了。
当然，对于计算机专业的人来说，那个在学习第一门语言的时候，大家肯定都实现过这样的问题的。
这里主要是提供一种思路，可以较为方便的处理这个问题。
如果你有更好的思路，可以告诉我。

-EOF-