【算法】Leetcode 第87场比赛回顾

一、背景

之前已经写了几场比赛记录了，如第88场、第101场、第126场、第127场、第128场、第129场比赛。
今天上午我做了第87场比赛，现在记录一下题解吧。

PS1：前三题用了半个小时就做完了，结果最后一题到时间结束也没做出来。
PS2：做题时不能分心，做最后一题时线上有个问题要处理，处理后回来思路就比较僵死了。

二、比较含退格的字符串

题号：844
题目：Backspace String Compare
地址：https://leetcode.com/contest/weekly-contest-87/problems/backspace-string-compare
源码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/87/A.cpp

题意：对于字符串，里面会有一个#代表退格字符。
给两个字符串，问使用退格字符处理之后的两个字符串是否相等。

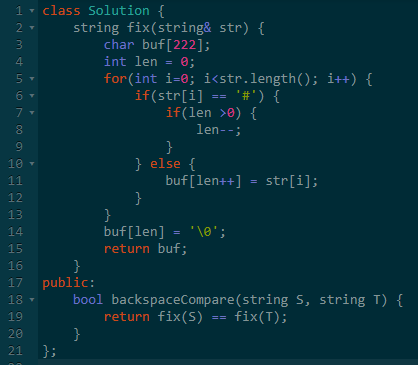
思路：分别处理两个字符串，然后判断即可。
处理字符串的时候，可以使用栈来处理。
有时候为了方便，直接使用数组模拟栈即可。

PS：字符串string也有数组的特征，所以直接使用string也可以。

三、数组中的最长山脉

题号：845
题目：Longest Mountain in Array
地址：https://leetcode.com/contest/weekly-contest-87/problems/longest-mountain-in-array/
源码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/87/B.cpp

题意：给一个数组，求最长的山峰。
山峰定义：长度至少为3的连续数组，前半部严格增序，后半部严格降序。

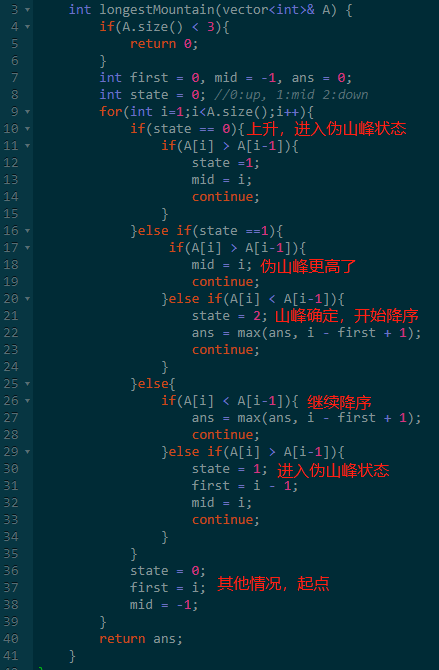
思路：第一种思路就是严格按照题意进行循环模拟。
此时相当于实现一个状态机，有三种状态。
状态一：只有起点，此时是升序。
状态二：有起点，有临时山峰，后面可能升序，也可能降序。
状态三：降序中，此时可以得到一个临时答案。
其他边界情况，都可以归属于状态一起点。

代码如下：

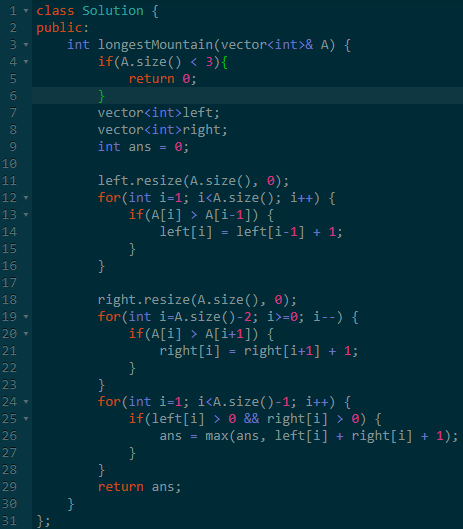
其实，这道题还有一种很简单的思路。
我们先扫描两边数组，分别计算每个点到两边降序的最长距离。
然后在扫描一遍数组，分别计算当前顶点为山峰时的最大距离。
结果取max即可。

四、一手顺子

题号：846
题目：Hand of Straights
地址：https://leetcode.com/contest/weekly-contest-87/problems/hand-of-straights/
源码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/87/C.cpp

题意：给一个序列，问是否可以分成多个分组，每个分组的大小是W，且是连续升序的数组组成。
连续升序的含义是相邻数字之差为一。

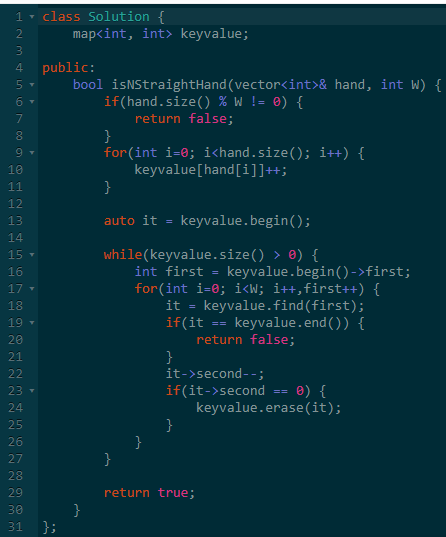
思路：既然数字可以随机选择，我们直接使用map计数储存即可。
每次从map中取最小的数字，然后分别判断后续连续w个数字是否存在，存在则更新计数。
最后map为空则代表有答案。

五、访问所有节点的最短路径

题号：847
题目：Shortest Path Visiting All Nodes
地址：https://leetcode.com/contest/weekly-contest-87/problems/shortest-path-visiting-all-nodes/
源码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/87/D.cpp

题意：给一个联通图，问从一个顶点开始遍历所有顶点的最小路径。

思路：这道题是经典的旅行商问题，当数据量较小的时候，解决方法很多。

我刚开始一看点的个数最多是12个，便使用dfs暴力搜索，结果超时了。
然后便想到使用状态DP来压缩状态，从而避免重复计算。

状态定义：F(start, state) 代表当前起点是start 且当前地图是state时，遍历所有顶点需要的最少步数。
地图state是使用bit位来保存每个顶点的状态，含义为当前顶点是否访问过。
状态转移：每次从当前起点，转移到相邻的边。

正常情况下，我们就可以通过dfs加状态DP解决这类问题了。
但是实际情况时，当图中有环时，这样就会导致死循环。
也是因为这个原因，最终我没有过这道题。

后来想到，问题出在状态转移上。
一个好的状态转移应该保证子状态是收敛的。
收敛的方法就是确保子问题个数是逐渐减小的。

比如对于地图state，子问题应该是比父问题多覆盖一个顶点。
这样递归下去就可以保证状态收敛（每次多覆盖一个顶点，顶多N次）。

这里我们状态转移的时候，不能转移到相邻的边，而应该转移到尚未访问的顶点。
所以，这里还需要预先计算出任何两个顶点的最短距离，这个使用flood算法即可解决。

解决dfs的死循环问题后，我开始想是否存在其他方法。
瞬间发现状态的定义稍微修改一下，就会有一个非常简单的方法。

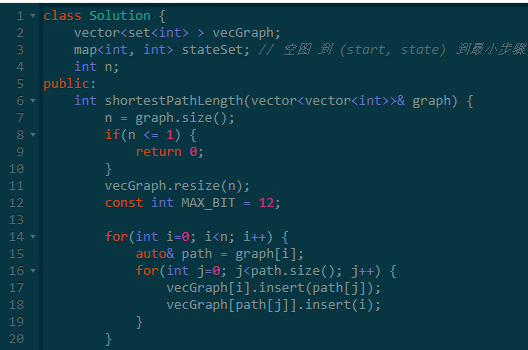
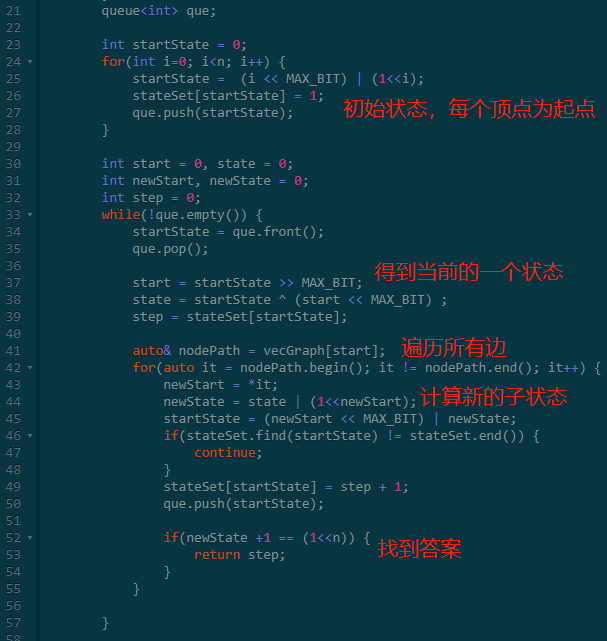
状态定义：F(start, state)代表空地图到达当前状态的最小步数。
状态转移：每次向相邻的边转移，判断状态是否存在，不存在则保存状态，存在则说明已经有最优值。

这不就是典型的BFS吗？
所以这里使用一个queue就可以解决问题了。

其实，这里还有一个问题：状态F(start, state)怎么储存呢？
由于两个数据都很小，我的方法是把两个数字使用位运算压缩到一个数字上，然后使用map记录其最小步数即可。

六、最后

其实这次四道题都不难，但是最后一道题我习惯性的使用DFS去搜索，结果就死循环了。
直到后来调整状态转移公式时，DFS才正常解决这个问题。
然后想其他方法时，马上就想到BFS。

可见第一印象、第一想法很重要。
一不小心先入为主，就会被带到坑里了，再想改变就很难了。

-EOF-