Leetcode 第94场比赛回顾

一、背景

之前写了不少比赛回顾了，如果你感兴趣，可以在公众号的历史记录顶部进行搜索，可以搜到所有的比赛记录。

今天，给你们分享几道相对来说比较简单的算法题。

题目地址：https://leetcode.com/contest/weekly-contest-94
源代码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/94

二、叶子相似的树

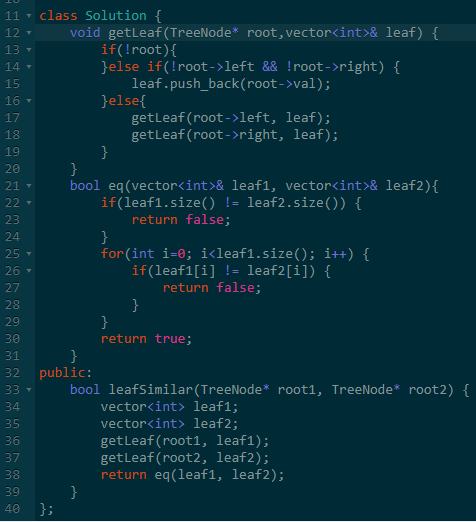
题意：给一个二叉树，二叉树的所有叶子从左到右可以组成一个叶子序列。
问两个二叉树的叶子序列是否相同。

思路：先分别递归求出两个树的叶子序列，然后比较序列即可。

三、模拟行走机器人

题意：一个机器人在一个无限大的网格（坐标系）里，起点在(0,0)，方向朝北，按照三个指令进行行动。
1、-1：向左转90度。
2、-2：向右转90度。
3、1<=x<=9：朝前移动x个长度单位。
附加规则：如果机器人向前移动的过程中遇到障碍物，将会在障碍物那里停下，等待下次指令。
问题：求机器人在移动过程中，离原点最大的欧式距离的平方。
注：欧式距离就是直线距离。

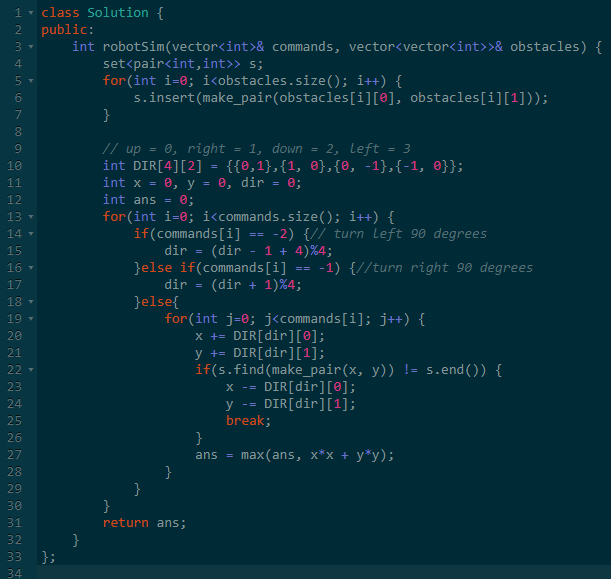
思路：按照指令模拟即可。
不过在移动的过程中，需要判断是否有障碍物，这个判断不能暴力判断。
由于是是判断一个点是否在一个坐标集合里面，可以使用set或者map将坐标储存起来，这样直接查找是否存在即可。
如果使用vector储存，那对数组进行排序，然后二分查找也可以。

不过现在都使用c++语言了，直接set+pair判断即可。

注：你在做这种坐标系相关题时，是不是需要上下左右进行各种判断，很容易写错？
使用我的DIR数组就不会有这个问题了。

四、爱吃香蕉的koko

题意：有N堆香蕉，每堆有一些。
koko 每小时可以吃K个香蕉，且每次只能选择一堆香蕉来吃，如果一堆不足K个，那就把这堆吃完就行了。 现在需要 koko 在H小时内把香蕉吃完，问最小的K是多少。

思路：假设我们知道 koko 的吃香蕉速度是k，怎么判断需要多少小时才能吃完呢？
这个没有捷径，每堆香蕉是独立的，所以只能循环一堆堆的判断累加。
所以判断一次的复杂度是O(n)。

现在是需要找到最小的k，枚举一个个判断的话，复杂度就是O(n*M)，M为所有堆中香蕉最多的数量。
那能不能更快的找到呢？

对于O(n)的复杂度，只能往O(log(n))或者O(1)的方向思考。

O(log(n))的话，自然就可以想到二分查找了。
这里枚举的过程中，枚举的结果有两个：可以吃完 与 不可以吃完。
对于这种场景，确实可以使用二分查找来加速查找。

如果使用O(1)的方法，那只能进行数学计算了。
方程大概是sum(piles[i]/k)<=H，面对这个方程，由于涉及到向上取整，还真没法一下就求解出来。
注：目前利用我掌握的知识，是无法找到快速求解方法的。

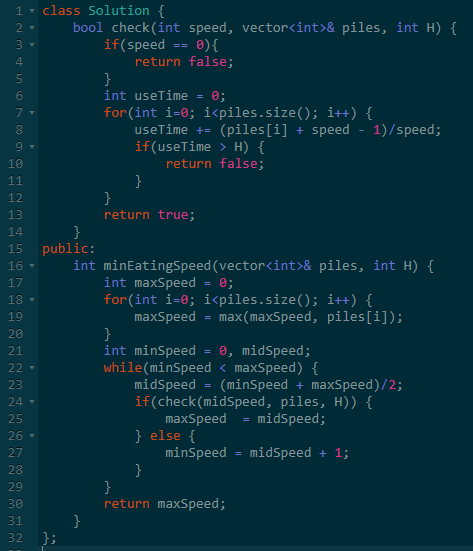
既然使用二分查找可以做，那就上代码吧。

五、最长的斐波那契子序列的长度

题意：告诉你一个严格递增序列，求一个最长的子序列。使得这个子序列满足斐波那契公式。
斐波那契公式：对于序列中任意连续的三个数字，满足val[i] + val[i+1] = val[i+2]。
最终只需要输出最长子序列的长度。

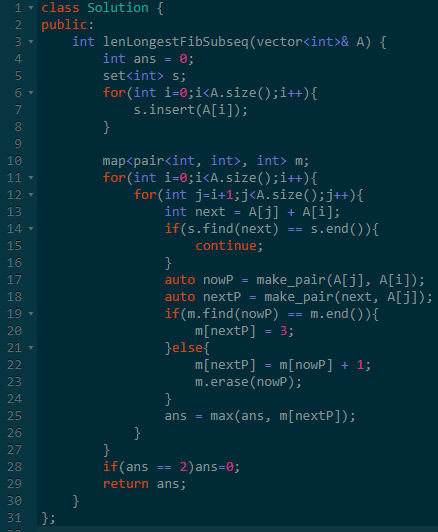
思路：对于子系列这种题，那只能进行枚举所有序列的前缀或者后缀了。
对于前缀，可以暴力查询以这两位为前缀的序列最长是多长，复杂度O(n^2*log(M))，M为序列里的最大值。
对于后缀，则是DP思想，储存所有合法序列最后两位为后缀的最大长度。

六、最后

好了，这次比赛涉及到树、模拟、二分、动态规划，建议大家练习一下。

-EOF-