Leetcode 第133场比赛回顾

一、背景

今天做了 Leetcode 的第 133 场比赛，题型涉及到队列搜索、动态规划、子序列以及字符串题。

上图是我的提交记录，看着题都会做，然而时间有限。
我用力的去敲代码，最终还是没能在结束比赛之前把代码全部敲完，最后一题在结束比赛半个小时后才敲出来。
我仰天长叹：我的敲代码速度太慢了。

后面真的有必要练习一下敲代码的速度。

题目地址：https://leetcode.com/contest/weekly-contest-133
源代码：https://github.com/tiankonguse/leetcode-solutions/blob/master/contest/133

二、距离顺序排列矩阵单元格

题意：给你一个矩阵以及一个起点，求所有点到起点的最小曼哈顿距离（|r1 - r2| + |c1 - c2|）。
输出的坐标按曼哈顿距离从小到大排列。

思路：每个点到起点的曼哈顿距离是可以直接计算出来的。
所以第一种方法是先计算出所有点到起点的曼哈顿距离，然后按曼哈顿距离对所有点排序即可。

第二个方法是使用常规的广度优先搜索：从起点开始一层层的计算每个点到起点的曼哈顿距离。
搜索的过程中，也就得到了答案。

三、两地调度

题意：有2N个人和两个城市，告诉你每个人分别到两个城市的代价。
现在需要将这些人平均分配到两个城市去，使得总代价最低。

思路：典型的动态规划题。
这道题使用数学语言来描述，就是告诉你2N个物品，选择与不选择都有一定的费用，求使用最低费用选择N件物品。

而动态规划的状态定义为dp(n, k)。
代表前n个人选择k个物品的最低费用。
对于第n个人，如果选择第k个物品，总代价为dp(n-1, k-1) + yes(k)
如果不选择第k个物品，总代价为dp(n-1, k) + no(k)
结果是两个选择里面的最大值。
复杂度O(n^2)

当然，这道题也可以使用贪心来做。
先来看两个人的情况：

如果A物品选择的费用低于不选择的，而B物品选择的费用高于不选择的。那我们肯定选择A而不选择B。

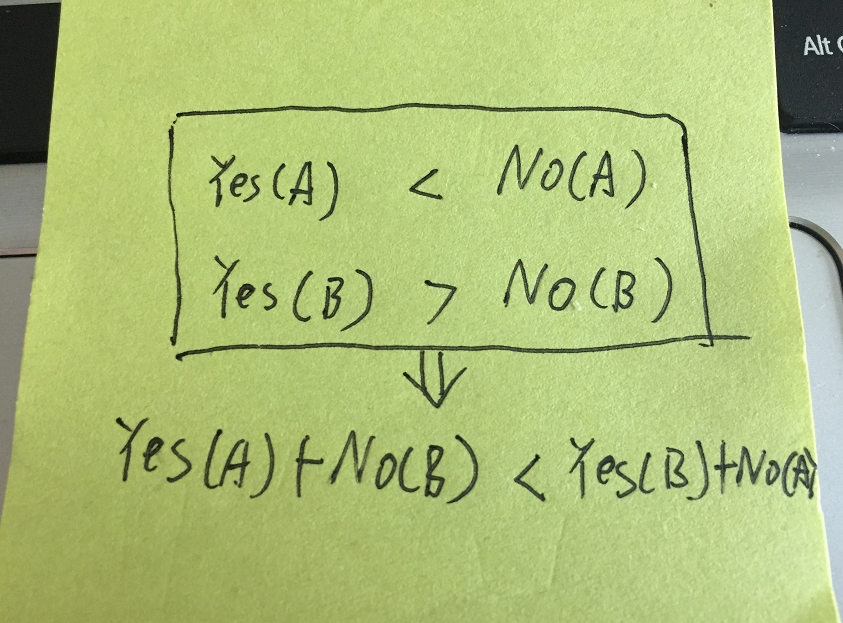
两个物品都是选择费用更大（不选择费用更大等价），那我们肯定选择差价小的那个物品。

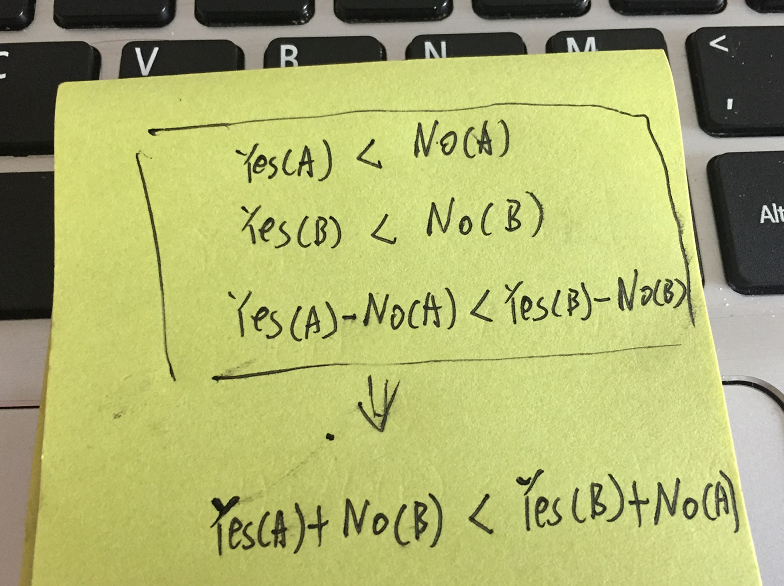
实际上，第一张图是第二张图的一种特殊情况，所以所有的物品都是要使用第二张图来挑选。
总结一下就是，先按差价排序，前n个挑选，后n个不挑选即可。
贪心复杂度，由于涉及排序，是O(n log(n))

四、两个非重叠子数组的最大和

题意：给一个数组，求两个不交叉的连续子数组，使得他们的和最小。
要求：子数组的长度一个是L，一个是M。

思路：最简单的方法就是暴力枚举所有连续子数组，然后找到最优答案。
别说，这种方法真可以过这道题。
如果不做任何优化的话，复杂度是O(n^2 * max(L,M))，肯定会超时的。
而枚举出两个连续数组的位置后，可以使用数组前缀和在O(1)内求出子数组和，这样就可以在O(n^2)内找到答案了。

另一种方法是扫描法。
即先预先计算出每个位置之前和之后，挑选一个长度为L的子数组的最小和，然后在计算长度为M的最小和。
然后扫面每个位置，假设在这个位置左边挑选长度为L的子数组，在右边选择长度为M的子数组，之和便是这个位置为分界线的最优值。
循环求出所有分界线的最优值，取最小即可得到答案。
复杂度O(n)。

五、字符流

题意：给一些单词，然后一些字符查询。历史上所有的查询组成一个字符串，问是否存在一个后缀，等于其中一个原始的单词。

思路：这道题我刚开始一直看不懂题意。后来耐心读题二十遍，终于看懂题了。
知道题意后，发现就是一个裸的 AC自动机 题。

AC自动机 是 Tire 树 和 KMP 结合的高级复杂结构。

下面先来看看 Tire 树吧。

tire树俗称字典树，一般储存的是纯小写字母，可以按26叉树来理解。
一般每个字母对应一个 child 指针，值就是当前的字母，还有一个 flag 来标记是否是字符串结束。

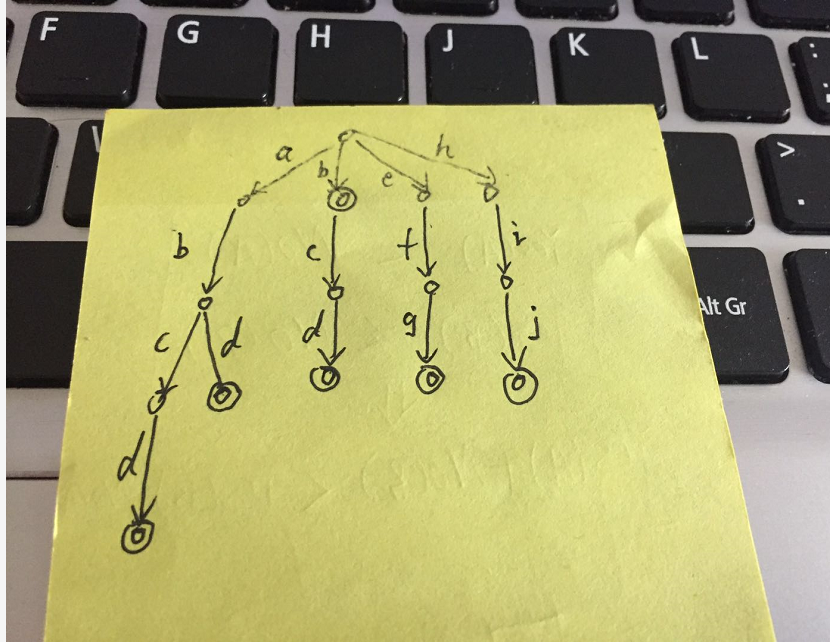
使用字典树的好处时，对于多个字符串，其公共前缀可以储存在一个节点上。
而我们查询一个字符串是否在字典树上时，从根节点递归查找下去。
如果直到最后一个字符都可以在字典树上找到，且最后一个节点也标记了字符串结束，则代表字符串存在，否则不存在。

如果我们想进行后缀匹配的话，就需要在 Tire 树的某次查询不匹配的时候，需要能够跳到下一个最长匹配的位置继续进行匹配。
这个思想和KMP的思想一模一样的，具有KMP思想的Tire树就是AC自动机。

我已经有五六年没写过 AC 自动机了。
虽说和KMP的next类似，但是剩下十几分钟就结束比赛了，我是有信心在这个时间内敲不出这个代码的。

所以我选择找其他的方法，毕竟条条大路通罗马嘛。

简单分析之后，发现是问后缀是否匹配单词，那将所有单词和查询的字符串翻转，是不是就是前缀查询了？
这样，翻转后，这道题就是赤裸裸额 Tire 树了。

可是，即使是Tire树，剩下几分钟了，我也不想敲了。
那有没有更简单的方法呢？
还真让我找到了，这个方法你们也都可以理解。

开始的时候，直接对输入的单词全部翻转，然后按翻转后的单词进行排序。
那这个排完序的单词列表其实和 Tire 没多大区别了。
不过Tire 树没有冗余前缀，而单词列表有冗余的前缀。

对于Tire，可以O(1)定位到下一个节点。
对于单词列表，在之前的区间基础上，使用二分查找O(log(n))来定位到下个节点区间。

如果不存在这样的区间，则代表没找到单词。
如果区间内已经有单词遍历到最后了，则代表找到了。

天呢，使用二分查找竟然实现了Tire树，看代码。

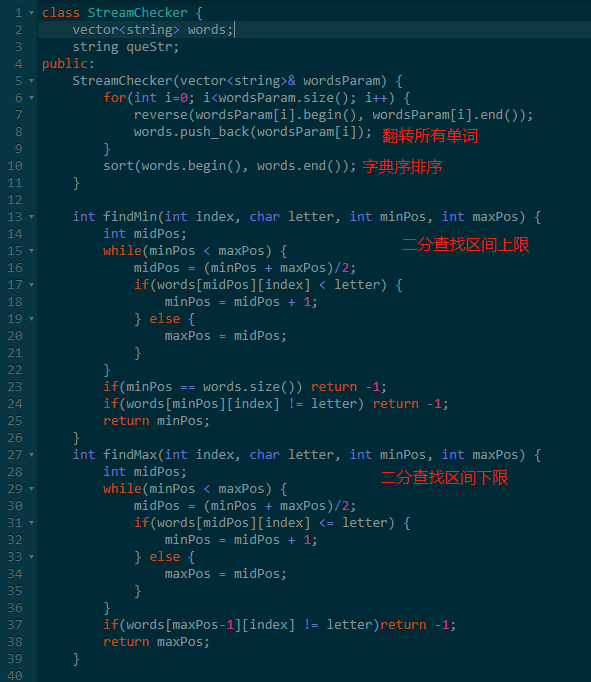
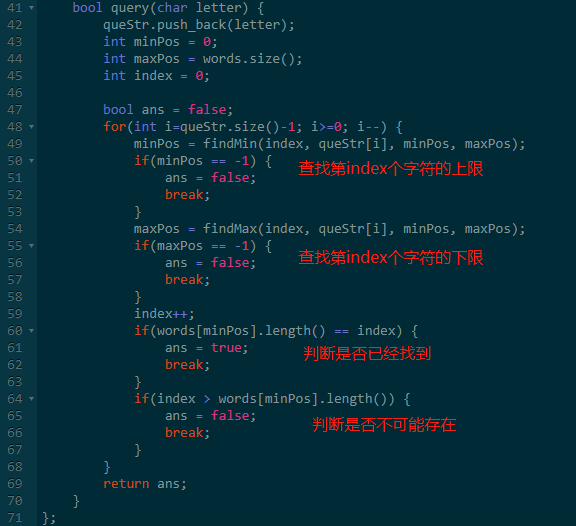
六、最后

回头想想，这次比赛每道题都有多种方法，我都是选择了实现方式最复杂的那种方法。
第一题排序就行了，我使用了队列广度优先搜索。
第二题排序贪心就行了，我使用的动态规划。
第三题暴力两层循环就行了，我使用的左右扫描法。
第四题 AC 自动机或者 Tire 树就行了，我使用的区间二分查找模拟 Tire 树。

这样看来，不仅仅是我敲代码的速度慢，还有我的方法不对。
虽然有思路，但是如果实现代码不简单的话，就需要很长时间才能实现。
所以以后做题的时候，多给自己一分钟想想有没有其他的方法。
这里多浪费一分钟，可能就给后面敲代码节省十分钟时间，有没有？

-EOF-