Leetcode第134场比赛回顾

一、背景

上周末因为五一调休加班，我没有参加比赛，现在来看一下这个比赛吧。

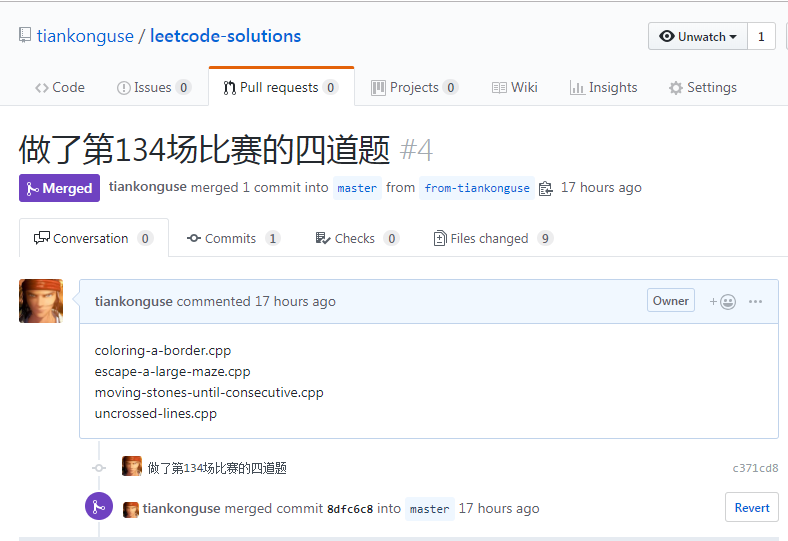
做完做了这四道题，顺便使用了一下 LeetCode 互动项目。

操作之后，发现杜宇首次使用 github 来协同工作的人来说，还是蛮有难度的。
如果你想学习算法的话，建议参考上一篇文章《启动Leetcode算法互动编程项目》来尝试一下。

如果你参与这个项目了，并参与了几轮互动编程。以后也可以说自己在 github 上参与过公开项目了，而且还多次进行 pull request 贡献代码了。

二、移动石子直到连续

题号：5039
题意：数轴上有三个不重复的数字x<y<z，每一步可以选择x或者z数字来移动，移动位置后的新位置是k，需要满足x<k<z && k!=y，直到无法移动，结束移动。
要求输出最大移动步数和最小移动步数。

思路：首先需要明白，无法移动的条件是三个数字连续，即x+1 == y && y+1 == z。
而对于最大步数和最小步数，方案有两种。

第一种方案是DP或记忆化搜索。
但是看到这道题难度是 easy，搜索和DP的难度至少是 Medium 或者 hard 的。
所以这道题肯定可以更简单的方法。

第二种方案就是贪心计算。

先开最大步数，每移动一下，x和z的距离至少减一，这样移动到距离是2的时候，就不能移动了。
所以最大步数是z-x-2。

对于最小步数，通常两步即可完成。
起始是x, y,z
第一步之后是x,x+1,y
第二步之后是x,x+1,x+2

但是，有时候需要一步就可以达到三个数字连续。 大概分这样几种情况：

1.x,x+1,x+2+n，此时最后一个数字移动到x+2即可。
2.x,x+2,x+2+n，此时最后一个数字移动到x+1即可。
3.两种对称情况，即后两个数字连续或者间隔为1。

只有一种情况需要0步，即三个数字本身就是连续数字。

小技巧：对于只有一步的情况较多，可以使用排除法，两步和零步的都计算了，其他的就是一步的。

三、边框着色

题号：5040
题意：给一个矩阵和一个坐标，求将坐标值相等的联通区域染色，这里只需要染色边界。

思路：如果是纯粹的染色，大家应该都会做，一个 DFS 或者 BFS 即可。
那只染色边界怎么办呢？
染色前判断一下是不是边界即可。

小技巧：新染色的值可能在矩阵上是存在的，有些人不知道怎么区分。
我经常使用的方法时先染色为矩阵上不存在的特殊值，最后再全部替换为目标值。

四、不相交的线

题号：5041
题意：给两个数组，两个数组之间相等的值可以相连。问不相交的线可以画几条。

思路：这道题就是一个赤裸裸的最长公共子序列题。
直接两层循环 DP 即可。

五、逃离大迷宫

题号：5042
题意：告诉你一个10^6 x 10^6大小的网格，以及一些坐标代表障碍物，问是否可以从一个起点到达一个终点。

思路：以前做过类似的题，不过矩阵较小，直接暴力搜索即可。
这里矩阵很大，没办法暴力搜索了。

那怎么判断两个点是否可到达呢？这个不好判断。
但是反过来，我们可以判断这个点是否不可达。
当障碍物将其中一个点围起来的时候，这个点就会变成不可达。

看看障碍物的个数，最多两百个。
不考虑边界，那这些障碍物最大可以围城一个50*50的闭环空间。
结合上边界，这些障碍物最大可以围城200*100的闭环空间。

看到这里，这道题的解决方案也就出来了。
我们分别查找两个点，如果在200*100步内依旧还有搜索空间，则认为这个点是开放的。
如果两个点都是开放的，则认为两个点是可以互相到达的。

六、最后

这次四道题还算简单，尤其是介绍思路后，大家都可以实现一下。

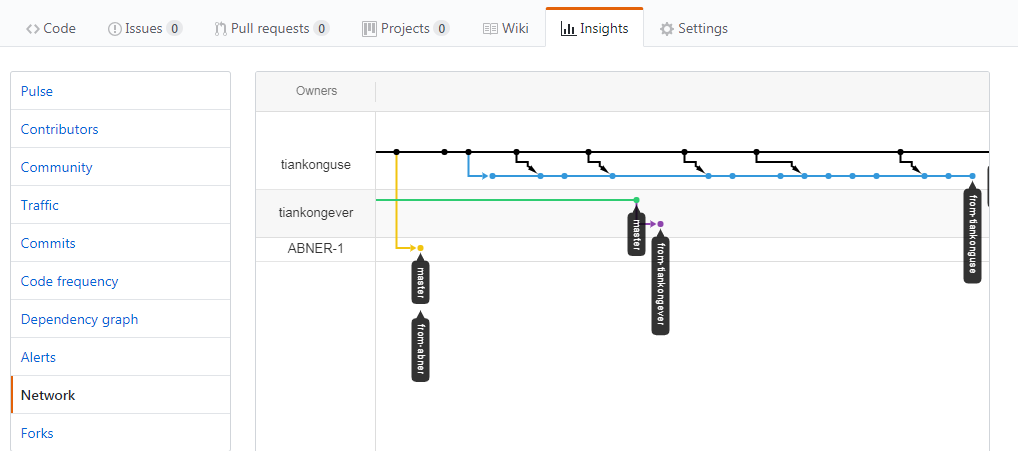
和几个人简单的互动后，发现 github 上的 network 图很好看，可以清晰的记录大家的互动情况。
你可以来尝试一下。

-EOF-