二叉搜索树就是这么简单-基础篇

一、背景

之前写过《数组》、《链表》、《队列与栈》、《哈希》、《二分查找》，后面就开始写树相关的文章了。

这里先介绍最简单的二分搜索树。

二、概念

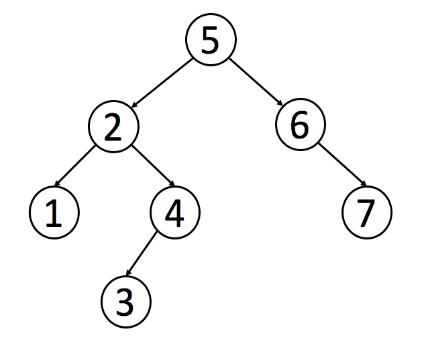
二叉搜索树（BST）是二叉树的一种特殊表示形式。

它满足如下特性：

1. 每个节点中的值必须大于或等于存储在其左侧子树中的任何值。
2. 每个节点中的值必须小于或等于存储在其右子树中的任何值。

二叉搜索树的概念了解了，就需要做一些练习题加深对这个概念的理解。

初级练习题：判断是不是二叉搜索树（题号 98）。
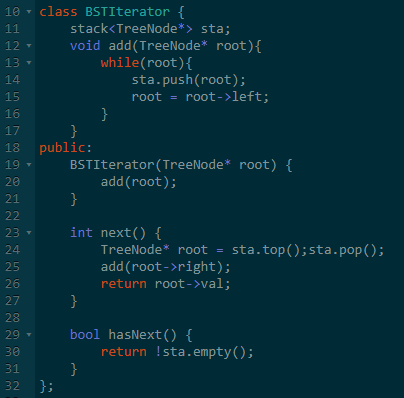
高级练习题：实现一个二叉搜索树迭代器，每次调用next时返回下一个最小值。

分析：找到最小值不难，关键是找到下一个最小值。

根据二叉搜索树的性质，下一个最小值有两种可能：一种是在右子树里面；如果没有右儿子则是父节点。
找到右子树的最小值不难，关键是怎么找到父节点。

如果你学过前面的《栈和队列》文章的话，应该可以发现，可以使用栈来储存父节点路径。
这样，下一个最小值就可以轻松实现了。

三、搜索

二叉搜索树主要支持三个操作：搜索、插入和删除。
这里我们先来看看搜索操作吧。

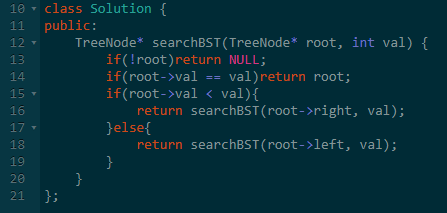
根据BST的特性，对于每个节点：

1. 如果目标值等于节点的值，则返回节点;
2. 如果目标值小于节点的值，则继续在左子树中搜索;
3. 如果目标值大于节点的值，则继续在右子树中搜索。

四、插入

二叉搜索树中的另一个常见操作是插入一个新节点。

有许多不同的方法去插入新节点。
这里我们只讨论一种最简单的方法。

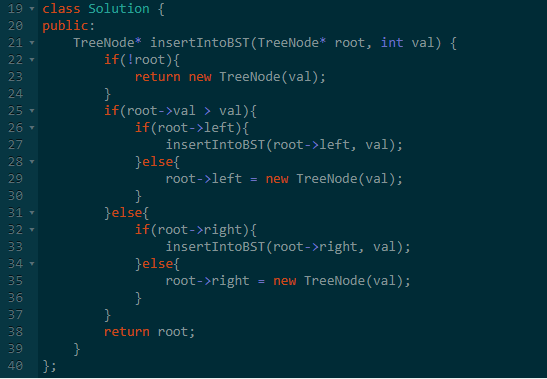
它的主要思想是为目标节点找出合适的叶节点位置，然后将该节点作为叶节点插入。

与搜索操作类似，对于每个节点，我们将：

1. 根据节点值与目标节点值的关系，搜索左子树或右子树；
2. 重复步骤 1 直到到达外部节点；
3. 根据节点的值与目标节点的值的关系，将新节点添加为其左侧或右侧的子节点。

这样，我们就可以添加一个新的节点并依旧维持二叉搜索树的性质。

五、删除

删除要比我们前面提到过的两种操作复杂许多。

根据其子节点的个数，我们需考虑以下三种情况：

1. 如果目标节点没有子节点，我们可以直接移除该目标节点。
2. 如果目标节只有一个子节点，我们可以用其子节点作为替换。
3. 如果目标节点有两个子节点，我们需要用合并两个子树为一个树，再删除该目标节点。

这里合并两个子树为一个树就有点复杂了。
作为基础篇这里就不多介绍了。

六、总结

二叉搜索树的优点是，即便在最坏的情况下，也允许你在O(h)的时间复杂度内执行所有的搜索、插入、删除操作。
有心的你应该注意到了，某些时候，树可能退化为一条链，这时候树的高度就是树的节点个数，此时复杂度就是O(n)而不是O(h)。
所以，这里需要一种机制，来保证树的高度不会退化为O(n)，应该始终为O(h=log(n))。

具体使用时，一般使用内置的数据结构map或set就够了。
如果涉及到较复杂的操作，那就需要采取实现一些机制，来保证树的高度不会退化。
常见的有平衡树、红黑树、AVL树、伸展树等等，后面到高阶部分了再给你们讲解。

-EOF-