Leetcode 第9场双周赛回顾

零、背景

周六晚上，QQ 算法群里有人反馈看不到题，也有人问搜索超时怎么优化。
我忘记双周赛了，所以没参加。

周日晚上找了个时间做了做，发现排序、统计、搜索、动态规划这些题型几乎在每场 leetcode 比赛上都会遇到。
而除了动态规划，前三个题型其实都很容易学会，这里我就简单的介绍一下吧。

一、最多可以买到的苹果数量

题意：给一堆苹果，每个苹果有一个重量。
现在给一个能够承重 5000 的背包，问最多可以放入多少个苹果。

思路：起初一看，很容易往 0/1 背包动态规划方向思考。
但是我一想，不对，这是第一道题，难度是 Easy，不可能是动态规划。

仔细一看题，要求是苹果的个数最多。
当然是有限选择重量最小的苹果了。

总结：先排序，然后从前到后一个个放，不能放了就结束。
题型：排序
复杂度：n log(n) + n

二、进击的骑士

题意：给一个无限棋盘和一个名字叫做马的棋子，问到达目标坐标的最小跳数。
细节：在象棋中，马是按日字型走的，即一个坐标移动一下，垂直的坐标移动两下。
这种移动方法有 8 种。

思路：对于最优答案，就需要使用广度优先搜索（BFS）了。
需要注意的时，需要记忆化搜索，即搜索过的坐标不能再搜索了。

那怎么标记坐标是否搜索过呢？
第一种是定义二维数组，值是状态，如默认是 false 代表没搜索，搜过后标记为 true。
第二种是使用 map 数据结构，key 是二元组，value 是对应的状态。
第三种还是 map ，这里 key 是按照一定规则计算出来的整数，value 是对应的状态。

这里我选择了第三种，毕竟 go 语言还不是很熟悉，map的 key 是否支持二元组还不知道，定义二维数组内存不好控制容易爆栈。

总结：BFS 记忆化搜索。
题型：搜索
复杂度：n^2

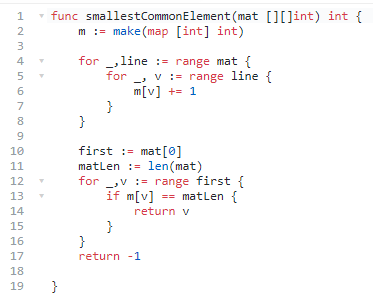
三、找出所有行中最小公共元素

题意：给一个矩阵，每一行已经递增。求所有行里面的最小公共元素。

思路：标准的做法应该是记录第一行的元素组成一个集合，然后在后面所有行来判断是否存在。
不存在则从集合中删除，最后剩下的就都是公共元素，最小的就是第一个。

但是使用 GO 语言来判断是否存在和删除操作挺不爽的。
我就直接先统计，然后看第一行元素的统计个数是否等于行数。
潜在问题：如果一行有重复元素，这个方法有问题。实际上不存在重复的。

总结：集合操作或者集合统计。
题型：数组统计
复杂度：n^2

四、建造街区的最短时间

题意：有一堆建筑要建造，这里给出了每个建筑的建造耗时。
最开始，只有一个工人。每个工人都可以使用克隆技术分裂为两个人，但是克隆有个耗时，耗时区间内这个人工什么都不能做。
另外，每个工人一旦开始建造建筑，就不能进行克隆了，而且一个人工只能建造一个建筑。
问建完所有建筑的最小耗时。

思路：首先肯定可以把所有建筑建造完的。

比如分两阶段。
第一阶段只克隆人，知道工人数量和建筑数量一样。
第二阶段开始干活，每人建一个建筑。

但是，我们分析之后，发现有些场景下分工合作。
即部分工人用于克隆分身，部分工人提早干活（比如耗时较旧的建筑提早开始建造），这样组合下去时间就会更短了。

至于哪种分工耗时最短我们不知道，所以我们需要遍历所有的情况，然后找出最优值。

当然，分工干活的原因是不同建筑的建造耗时不同。
如果需要分工，那自然是优先建造耗时最久的建筑。
所以这里需要对建筑的耗时进行排序，使得可以快速找到建造耗时最长的建筑。

前面说的可能有点抽象，这里来具体分析问题。
假设我们有 n个建筑，m个工人。 可以选择的决策有：

0 个人干活，m 个人生孩子，剩余建筑 n 个。  
1 个人干活，m-1 个人生孩子，剩余建筑 n -1 个。  
...
m-1 个人干活， 1 个人生孩子， 剩余建筑 n - m + 1 个。  

使用公式来表示，即 i 个人干活， 则可以表示为：

f(n, m) = min( F(n, m, i) )
0 <= i < m

i个人干活时，他们的耗时是固定的，即木桶短板理论，干活最慢的耗时就是总耗时。
所以F(n , m, i)的公式如下

F(n, m, i) = max(Data[n] , f(n - i,  2 * (m - i)))

此时，可以发现，我们的推理公式已经形成了闭环。
但是复杂度是O(n^3)的，所以这种方法会超时的。

复杂度推理：n是一个维度，m是一个维度，i是一个维度。三个维度合起来就是n^3了。

前两个维度在这种思维模式下，已经没有优化空间了。
但是第三个维度，倒是可以进一步分析。

对于i的循环，我们可以展开来看，或发现有不少重复计算。
展开如下

i=0, f(n, 2 * m)  
i=1, f(n - 1, 2 * (m - 1))
i=2, f(n - 2, 2 * (m - 2))
...
i=m-1, f(n - (m - 1), 2)

我们目标是找到所有i里面的最小值。
这个其实可以转化为另外一个递归公式：

M(n, m) =  min(f(n, 2m), M(n - 1, m - 1))

此时，我们可以将M(n, m)的计算结果也保存下来。
这样就可以在O(1)时间内找到最优值。

总结：典型的动态规划题，不过需要拆分为两个动态规划公式。
第一个是矩阵的问题拆分，一个是最优值的问题拆分。
这两步都想到了，这道题就可以做出来了。
题型：动态规划
复杂度：O(n^2)

五、最后

这次比赛的题挺好的，排序、统计、搜索都比较基础，而动态规划则比较经典。
建议大家都做一下。

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code