有限制的随机数（矩阵状态机）

一、背景

之前在《Leetcode 第 158 场比赛回顾》文章中，第三题介绍了动态规划的递归解法。

后来在《有限制的掷骰子（递推版）》分享了递推的实现，然后使用预处理进行时间优化，使用滚动数组进行空间优化。

在递推的解法中，提出了一个很重要的结论：状态转移方程的状态n只与状态n-1有关系。

就是这样一个结论，里面暗含着另外一个更高级的做法：矩阵状态机优化法。

二、回顾

题意是有n次机会来随机生成数字，每次随机出的数字是1~6。
但是有个限制，相同的数字连续出现的次数有个限制。
问最终生成的合法的数字序列有多少种。

我们也推理出了一个递归状态：f(k, index, n)，代表数字index在前面出现k次时，再掷n次骰子会出现多少序列。
这个状态可以使用递归实现非常简单。

其实，上篇文章我少说一句，那就是使用递推实现的时候，状态f(k, index, n)的含义是掷n次骰子后，以k个index为后缀的序列个数。
由于是后缀的个数，所以我们需要求和统计所有后缀的个数。

三、矩阵状态机

现在我们聚焦在n与n-1两组状态上，则发现状态的关系是固定的。

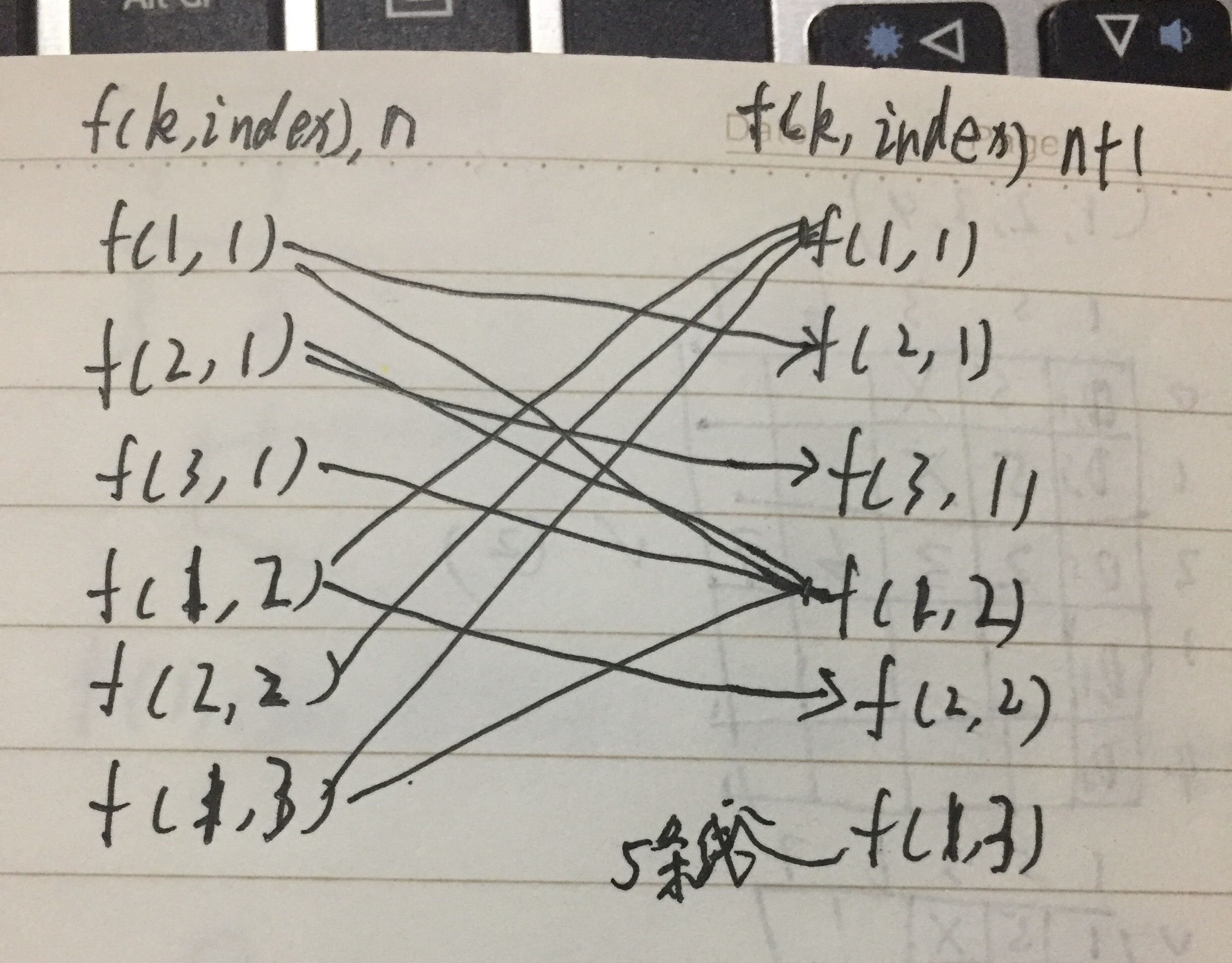
如上图，状态f(1,1)可能来自所有的f(x, ~1)，而状态f(2, 1)只可能来自于f(1, 1)。

使用几何意义来表示就是：
第n+1轮的f(1,1)，只能来自第n轮的不以1为后缀的所有状态答案之和。
第n+1轮的f(2,1)，只能来自第n轮的f(1,1)的状态答案。

这些状态之间的关系实际上可以使用0/1矩阵表示，然后通过矩阵运算就可以得到下一轮所有状态的答案了。

为了简单起见，这里假设只有2个数字，最多都只能出现2次。

则有四个状态，分别编号为0~3。

0: f(1, 1)
1: f(2, 1)
2: f(1, 2)
3: f(2, 2)

则状态机的关系是下图

  | 0 1 2 3
- - - - - -
0 | 0 1 1 0
1 | 0 0 1 0
2 | 1 0 0 1
3 | 1 0 0 0

矩阵(i, j)为1时含义为状态i能够到达状态j。

这个矩阵竖着按列看比较容易理解。
比如状态0和状态2，可以看出来相同数字后缀的状态都是0，不同数字后缀的状态都是1
而对于状态1和状态3，则只有一个值是1，那就是状态i的下一个状态，即满足j=i+1的时候才为1。

有了这个矩阵状态机，我们就可以快速求出任意次数后，各状态的个数了。

例如起始状态中，后缀只出现一个数字的状态值为1。
原因也很简单，只随机出一个值。

  | 0 1 2 3
- - - - - -
0 | 1 0 1 0

随机第二次的时候，起始状态乘以状态矩阵，就可以得出第二次的结果了。

如上图，随机第三次，第四次都可以很快的计算出结果。

所以，想求第n次的结果，起始状态乘n-1次这个矩阵状态机就行了。

四、矩阵幂优化

我们知道，矩阵满足结合律，即(A * B) * C等价于A * (B * C)。
所以起始矩阵乘以n-1个矩阵状态机，等价于乘以矩阵状态机的幂，即先求出矩阵状态机的幂。

对于幂的运算，可以通过二进制优化来加速运算，这样n个矩阵相乘，我们就可以优化为log(n)个矩阵相乘了。

理论大概如下：

2 ^ 15
= 2 ^ (1 + 2 + 4 + 8)
= 2^1 * 2^2 * 2^4 * 2^8

2^8 = 2^4 * 2^4
2^4 = 2^2 * 2^2
2^2 = 2^1 * 2^1

本来需要乘15次矩阵的，这里通过乘2*log(15)次计算出结果来了。

空间复杂度：(6*15) ^ 2
时间复杂度：log(n) * (6*15) ^ 3

五、最后

根据时间复杂度可以发现，这个矩阵状态机的方法并不比前面的递归和递推更优。

原因是次数n太小，log效果不明显，而转化为矩阵后，状态比较多，矩阵运算复杂度也比较高。

这样就导致这道题的耗时比较高。

但是这个方法可以学习一下，如果次数n改成一亿，前两个方法都不行了，但是这个方法可以轻松计算出答案来。

总结下就是满足三个条件时可以使用矩阵状态机：

1）当前状态只与上一个状态有关系
2）状态的维度很小
3）状态转移的次数很大时，递推会超时

关于矩阵状态机，你学会了吗？

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code