Leetcode 第 16 场双周赛回顾

零、背景

上周六晚上有一场 leetcode 的上周赛比赛，今天看了下，题解分享给大家。

一、替换为右边的最大值

题意：给一个数组，每个位置的值需要替换为数组里这个位置右边的最大值。
当然，最后一个元素右边由于不存在元素，值按-1处理。

思路：从右到左循环找到当前后缀的最大值即可。

二、使修改的数组和最接近目标

题意：给一个数组和目标数字。
你可以选择一个数字A（与数组的值无关），然后把数组中所有大于A的值修改为A。
问可以使数组之和最接近目标的最小的A。

思路：

方法一：

最简单的方法就是从大到小暴力枚举所有合法的答案A，挑最小的即可。
复杂度：O(n^2)

方法二：

暴力枚举的时候，有两层循环，第一层是枚举A，第二次是计算数组和。
其实，数组和可以通过排序后数组的前缀和来快速计算的。

具体来说就是先对数组排序，计算前缀和。
然后枚举A时，二分查找找到第一个大于A的位置pos。
这个位置之前的都不需要修改，之后的值都需要修改为A。
所以数组和就是sum[0, pos-1] + A * (len - pos)

复杂度：O(n log(n))

方法三：

再看看二分查找与从小到大遍历，其实两个可以结合在一起的。

比如数组的值是[5,10,15,20]
枚举值是A=[0,4]时，可以确定pos=1。
而枚举值是A=[5,9]时，可以确定pos=2
依次递推，二分查找的pos其实和枚举值是有固定的有序的映射关系的。

所以可以在遍历枚举值时，直接计算出pos的位置。
复杂度：O(n)

方法四：

再看看枚举值与和的关系，发现是严格有序的。
所以枚举值也可以进行二分处理，分别找出小于等于目标的最大值 和 大于等于目标的最小值，然后再二分找到数组的下标。

复杂度：O(log(n)^2)

方法五：

上面一个方法里面，由于求得是差的最小绝对值，所以使用了二分分别求上界与下界。
递增的绝对值其实就是一个类似于抛物线的折线，可以使用三分来完美解决。

复杂度：O(log(n)^2)

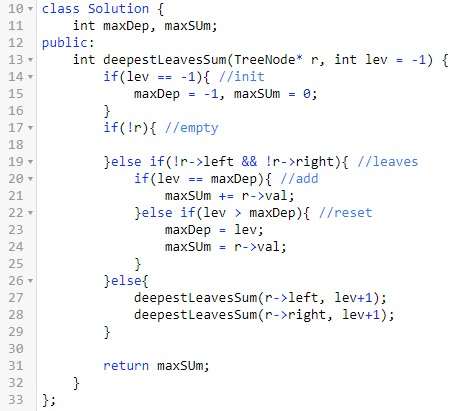
三、最深叶子之和

题意：给一个二叉树，先找出最深的叶子的高度，然后求这个高速的所有叶子之和。

思路：DFS遍历二叉树即可。

遇到更深的高度了，重置叶子和。
遇到相同的高度了，累加叶子和。

四、最优路径的数量

题意：给一个网格，有些格子有一个数字字符，代表路过这个格子的得分。 还有些格子有一个X字符，代表这个格子禁止通行。
每次只能向左、向上、向左上走一步。

求从右下角走到左上角的最大分数。
这个最大分数可能有多个路径，还需要求路径个数。

思路：最基本的动态规划题。

由于右下角到左上角 与 左上角到右下角完全对称，我们可以按后者来看这道题。

首先有一个贪心的性质在里面。
假设从起点到终点的一个最优路径经过了[x,y]，那么这个最优路径肯定由起点到[x,y]的最路径与[x,y]到终点的最优路径组成。

这个贪心性质也是划分子问题的关键所在。

由此，可以定义dp[i][j]代表从起点到[i, j]的最优路径以及个数。
而dp[i][j]由dp[i-1][j-1]、dp[i-1][j]、dp[i][j-1]三个来源计算而来。

计算方法上面的题遇到过，先看是不是更优，更优了则更新，相等了了相加，其他情况忽略。

五、最后

这次比赛第二题倒是有点意思，第三题和第四题分别是对应题型的基础题，基本功可以得话应该都可以做出来吧。

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code