leetcode 第 201 算法比赛

零、背景

今天正常参加了 leetcode 比赛，结果被第一题虐了，第一题花的时间最长。

一、整理字符串

题意：给一个字符串进行整理，整理好的字符串需要满足，相邻的字母不是一个大写一个小写的相等字母。

就这样一个问题，我硬是没看懂，研究了五十分钟。

梳理规则：连续两个的字母相同，但是大小写不同，则两个字母都删除。

思路：按照题意模拟即可，连续两个不满足要求，删除即可。

二、找出第 N 个二进制字符串中的第 K 位

题意：给一个规则构造出一个字符串数组，求第N个字符串的第 K 位的值。

构造规则如下图：

思路：通过分析可以得到三个结论。

1、第 i 个字符串是第 i+1 个字符串的前缀
2、除了第一个字符串，其他字符串长度都是奇数，中间位置值为 1。
3、所有字符串是镜像翻转对称的，即镜像位置的值一个是0一个是1。

有了上面三个结论，发现答案可以递归实现。

分析 K 在第 N 个字符串中的位置，大概分三种情况：

1、如果 k 在字符串的前半段，则答案与第 N-1 个字符串答案相同。
2、如果 k 在字符串的中间，则答案为 1。
3、如果 k 在字符串的后半段，则答案与第 N 个字符串的镜像位置相反。

三、和为目标值的最大数目不重叠非空子数组数目

题意：给一个数组和目标数，问数组能分拆分为若干个连续子数组，每个子数组的和都是目标。
如果可以，求最多可以拆分为多少个子数组。

思路：典型的动态规划题。

dp(i)代表前i个数字满足情况的子数组数。

面对第i个数字，分两种情况，选择与不选择。
选择的话，就需要找到以i为后缀且和为目标数的最短子数组，然后递归求出再之前的数组的答案。
不选择的话，答案就是dp(i-1)。

可以看到，代码非常简洁，初始化，dfs 递归计算即可。

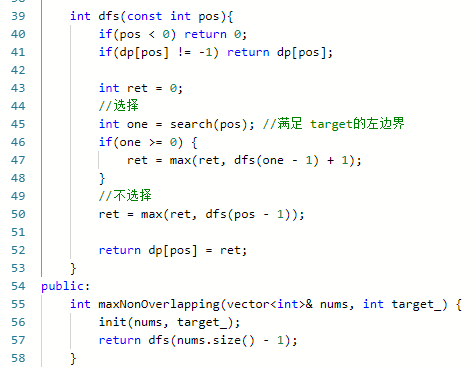
那如何找到以i为后缀且和为目标数的最短子数组呢？
假设最短子数组的其起始位置是 a，那么 [a, i] 的和就是目标数。

那怎么找到最优的位置 a 呢？
这就需要看从位置 a 可以得到哪些推论。
其实也就一个，那就是 [a, n) 的后缀和是固定的，即为i+1的后缀和加上目标数。

设[a, n)的后缀和为 S。 问题就转化为了寻找后缀和为 S 且值不大于 i 的数字。

如果预先计算所有的后缀和以及对应的位置，然后二分查找即可快速找到答案。
我是使用 cpp 实现的，所以直接使用 STL 中 set 的 upper_bound 即可。

四、切棍子的最小成本

思路：给一根棍子，以及 k 个不同的位置。
每次我们可以选一个位置将位置所在的棍子分为两段，代价是当前棍子的长度。
问 k 个不同的位置都选择之后，总代价是多少。

思路：刚开始可能想贪心，比如按长度的中位数或者位置的中位数。
但是我们不能证明其正确性。

再看看数据范围，k 只有不到 100 个。
使用动态规划的话，复杂度是 O(n^3)，不会超时。
那就选择动态规划了。

状态定义：dp(l, r)，区间为[l,r]的棍子里面的位置都选择后，最小代价是多少。

状态转移：枚举区间内的所有位置，取最小值。

优化：怎么快速找到区间内的所有位置呢？
可以先将所有位置排序，然后二分查找就可以找到两个位置的边界了。
当然，在递归的时候，直接维护好位置的边界也是可以的。

五、最后

回顾这次比赛：

第一题字符串题，题目绕点。
第二题数学题，递归或者递推循环即可。
第三题二分查找与动态规划题。
第四题二分查找与动态规划题。

这些题都不难，比较基础。

思考题：最后一题能贪心吗？

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code