leetcode 2021 春季编程大赛

零、背景

2021年04月05日，参加了 lleetcode 2021 春季编程大赛个人赛。

前面三道题比较简单，第四题被卡超时了，第五题想到线段树的方法，但是没时间做了。

现在 leetcode 的春赛已经是全国知名的比赛了，大部分知名算手都参加了。

建议大家都看下这些题，对于面试题，也有一定的代表性吧。

比赛地址：
https://leetcode-cn.com/contest/season/2021-spring/problems/4xy4Wx/
排行榜：
https://leetcode-cn.com/contest/season/2021-spring/ranking/solo/
源代码：
https://github.com/tiankonguse/leetcode-solutions/tree/master/season/2021-spring/person

一、采购方案

题意：给 N 个零件的价钱，只能购买两个零件。
问指定的预算，有多少种购买方案？

思路：签到题。

最暴力的方法是枚举所有零件对。
复杂度：O(n^2)
应该会超时。

优化1：二分查找

假设一个零件确定了，另外一个零件的选择范围是某个前缀。
这个前缀的边界可以通过二分查找找到。

复杂度：O(n log(n))

边界1：一个物品不能选择两次.
边界2：两个物品之间没有顺序。

int purchasePlans(vector<int>& nums, int target) {
    ll ans = 0;
    sort(nums.begin(), nums.end());

    int n = nums.size();
    for(int i=0;i<n;i++){
        if(nums[i] >= target) break;

        int dis = target - nums[i];

        auto it = std::upper_bound (nums.begin(), nums.end(), dis); 
        int num = std::distance(nums.begin(), it);
        if(i < num){ // 不能选自己，减去一个
            ans += num - 1;
        }else{
            ans += num;
        }
    }

    return ans/2 % 1000000007;
}

优化2：双指针

分析可以发现，每次二分查找的位置都是递增的。
所以可以记录上次的位置，在那个基础上继续查找。

复杂度：O(n)

for (int j=n-1,i=0;i<n;i++) {
    for (;j>i && a[i]+a[j]>target;--j);
    if (j<=i) break;
    ret=(ret+j-i)%MOD;
}

二、乐团站位

题意：给一个 n*n 的正方形，9 个数字如下图环形排列。
求指定下标的数字。

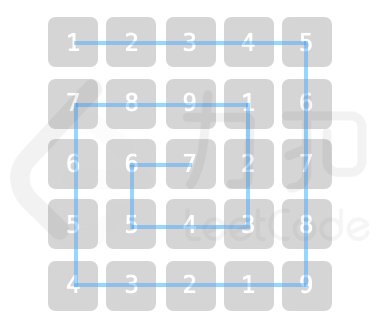
思路：

其实我看错题了，以为给的正方形总共 10^9 个数字，这样边长就是sort(10^9)。
这样模拟一层层去掉最外层，就可以计算出答案了。

复杂度：O(sqrt(n))

但是后来发现，正方形的边长是10^9，这样复杂度就变成了O(n)了。
超时了几次。

后来看清题意后，只好去推公式。

模拟去掉一圈数字，边长 n 减2，数字个数偏移4*(n-1)个。
根据坐标离边界的距离，可以计算出去掉几圈数字。
然后就可以把坐标移动到最外层了。

复杂度：O(1)

PS：这道题由于是由原先模拟一圈修改成模拟去掉 k 圈，很多地方没修改过来，WA 了无数次。
最后在本地把边长为 5 的所有坐标对应的测试数据都整理出来后，才调试找到所有的错误。

class Solution {
  ll mymin(ll a, ll b) { return a < b ? a : b; }
  int solver(ll n, ll x, ll y, ll start) {
    ll lev = n; // 边界，可以去掉几圈
    lev = mymin(lev, x - 0 + 1);
    lev = mymin(lev, n - x);
    lev = mymin(lev, y - 0 + 1);
    lev = mymin(lev, n - y);
    lev = lev - 1; 

    // 等差数列，计算出偏移量
    // 4 * (n-1) + 4 * (n-2) + .. + 4 * (n - lev)
    ll pos = 4 * ((n - 1) + (n - 1 - (lev - 1) * 2)) * lev / 2;
    start = (start + pos) % 9;
    x -= lev; //坐标修正
    y -= lev;
    n -= lev * 2; //边长修正

    if (x == 0 || y + 1 == n) {  // 上
      return (start + x + y) % 9;
    }
    if (x + 1 == n || y == 0) {  // 下
      return (start + 4 * (n - 1) - y - x) % 9;
    }
    return 0;
  }

 public:
  int orchestraLayout(int num, int x, int y) {
    return solver(num, x, y, 0) + 1;
  }
};

三、魔塔游戏

题意：给 N 个房间，里面可能有怪物，也可能有血瓶。
怪物会消耗血，血瓶会加血。
起始血量是 1，依次遍历所有房间，问是否可以活到最后（血量始终大于0）。

考虑到可能无法复活，现在可以作弊把某个房间放到最后面去。
问最少作弊几次才能活到最后。

思路：整个比赛最简单的题，一个最小堆即可解决。

具体来说，依次求前缀和。
遇到血量不够了，从前面找一个减血最多的怪物，把血加回来（放到最后再减）。
怪物加回来的血最后都要还回去，最后比较大小即可。

复杂度：O(n log(n))

int magicTower(vector<int>& nums) {
    min_queue<ll> que; //维护一个最小堆
    ll sum = 1;
    int ans = 0;
    ll left = 0;
    for(auto v: nums){
        if(v == 0) continue;
        if(v < 0){
            que.push(v);
        }
        sum += v;

        if(sum >= 0) continue;

        sum -= que.top();
        left += que.top();
        que.pop();
        ans++;
    }
    return sum + left > 0 ? ans : -1;
}

四、变换的迷宫

题意：给一个二维迷宫，之后每一时刻迷宫会发生变化。
问是否可以从左上角到达右下角。

有两个特殊技能，每个技能只能使用一次。
特殊技能1：临时将一个陷阱设置为空地。
特殊技能2：永久将一个坐标设置为空地。

数据分析：
时间范围：100 个时刻
迷宫大小：50*50
技能：2 种状态

思路：一开始一看数据范围，复杂度大概是O(100*50*50*4)，不会超时。
状态就是f(t, x, y, state)

敲完后，发现技能2有问题。
技能2是永久将一个坐标设置为空地，那这个坐标也是一个状态，需要保存下来了。

那计算一下这时候的状态个数呢？
状态：f(t,x,y,state,xx,yy)
复杂度：O(5w*5w)

我当时使用的广搜做的这道题。
所以我尝试使用启发式搜索，即队列改为优先队列。
但是依旧超时了。

赛后看了第一名楼教主的代码。
发现教主使用了贪心，即一旦使用了技能2，只能一直呆在原地。
一旦走出去，就不会再回来。
不再回来的意思是忽略技能2这个状态与坐标。

我思索这为什么要这样，后来想明白了。
如果出去转一圈，最终又转回来，那和一直呆在原地是等价的。

有了这个贪心，状态一下就又转化到了1000*1000的范围，就可以做这道题了。

这里就不贴代码了。

五、批量处理任务

题意：给一些任务可以运行的时间区间[low,up]，以及运行时长t。
任务可以拆分为无限个时间区间来运行。
现在有一个电脑，可以并发运行这些任务，问最短多长时间可以运行完所有任务。

思路：很容易想到通过贪心来做这道题。

即第一次运行电脑时，越晚越好。
因为运行的早了，可能只能几个任务并发运行。
而晚点运行，可以一起运行更多的任务。

不知道大家小时候是否玩过算盘，把一边向下后，由于重力作用，所有珠子都会落到另一边。

现在，我们把每个任务当做有时间刻度的柱子，时间区间当做柱子的长度，运行时长当做珠子的个数。

大概像下面的样子。

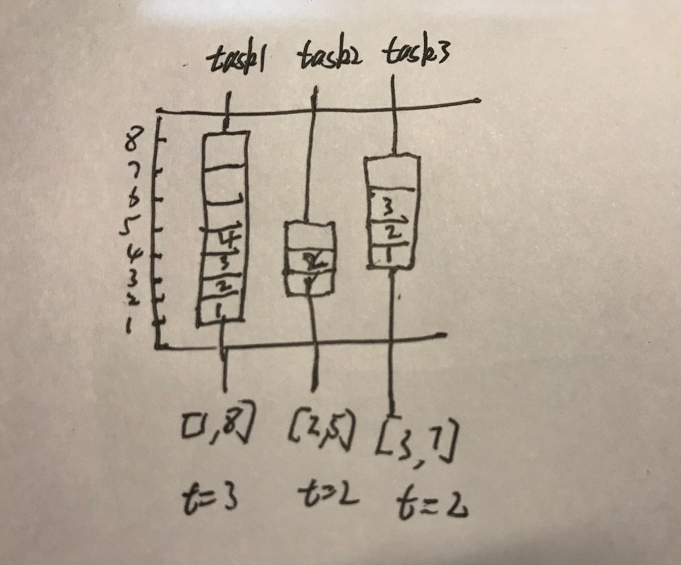
把这个特殊的算盘，顶部朝下，最顶部的珠子那一个任务就是需要贪心运行的。
如下图，可以找到贪心的起始时刻。

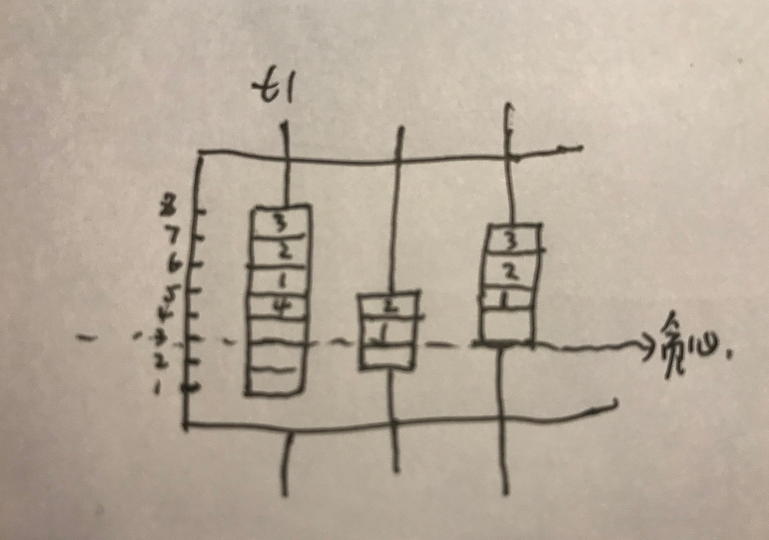
找到贪心任务后，电脑运行时刻也确定了。
所以这时候再把算盘反转过来，就可以看得一清二楚。

贪心的任务确定底线时间和上限时间。

想到这里，我第一时间想象到的是线段树。

通过线段树，可以查到贪心运行的时间点和任务，假设是任务 task。
贪心找到任务后，运行时长也确定了，为 task.t。

之后呢，需要对所有任务进行修改操作。

任务分三类：

第一类：起始时间小于等于底线的任务。
第二类：起始时间大于底线但小于等于上限的任务。
第三类：起始时间大于上限的任务（无关任务）。

对于第一类任务，由于对齐了底线，可以理解为时间区间要执行满，或者当前任务执行完。
对于第二类任务，由于没有对齐底线，只执行部分时间。

怎么找到这三类任务呢？
如果所有任务已经按照起始时间升序排序，就可以使用二分查找到了。

找到三类任务后，第一类直接区间操作，批量降低时长即可（运行完的，标记无效任务）。
对于第二类任务，由于不是满的，需要循环一个个处理（复杂度可能会退化）。

可能测试数据比较弱，就这样，就可以通过这道题了。

由于代码量比较大，这里就不贴代码了。

另外看其他人的代码，可以发现有各种各样的做法。
有按结束时间排序的，也有按起始时间排序的，也有不用线段树直接贪心的。
你怎么理解这道题的，可以分享一下？

六、最后

这里比赛，只有最后一题比较有技术含量，大部分人应该都做不出来。
而其他题，大家花个几个小时，应该都可以做出来。

这次比赛你做了几道题呢？

加油，算法人。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code