atcoder abc 第 243 场算法比赛

零、背景

这周六正常参加了 atcode 的 abc 比赛。

最后一题扩展题学不动了，其他题都会做了。

A - Shampoo

题意：有 V 升洗发水，三个人每天按固定顺序轮流洗一次头，分别使用若干洗发水。
问未来的天数里，谁洗头时先遇到洗发水不够了。

思路：三个人一天用的洗发水固定，求和取模，之后依次判断到谁的时候不够了。

B - Hit and Blow

题意：给两个长度相等的数组，有两个询问。

1）相同位置值相等的个数。
2）不同位置值相等的个数。

思路：

问题1，循环一遍相同位置比较就可以得到答案。

问题2，先统计一个数组值出现的次数，遍历另外一个数组，如果相同位置值不同时，加上对应值统计的次数即可。

C - Collision 2

题意：n 个人在滑冰场滑冰，速度相同，方向只会向左或向右。
告诉你每个人的坐标和方向，问是否会有人相撞。

思路：

由于只有两个方向，n 个人按 y 坐标进行分组，每组独立判断。

对于一个分组，先进行排序，然后从左到右扫描。
一旦有人方向向右，之后的人方向必须向右，否则就会相撞。

D - Moves on Binary Tree

题意：有一个无限的二叉树，起点在根节点，编号为 1。
有三个移动操作执行：向上、左二子、右儿子。
现在告诉你一个移动操作命令列表，问最终编号是多少。

注意事项：最终答案保证不大于 10^18 ，但过程中不保证。

思路：

注意事项很清楚了，不能无脑的去模拟。

这里需要做一个特殊的标记。
如果编号大于 10^18时，编号不真实变大，额外记录层数，即进入儿子加一，进入父亲减一。
层数为0时代表，正常的操作。

E - Edge Deletion

题意：给一个连通图，问最多删除多少边，可以使得子图内任意两点的最短路不变。

思路：

比赛的时候，一直在怀疑不同边之间可能会互相影响。
赛后看了题解，发现不会互相影响。

证明如下：

对于一条边的两个顶点，如果存在其他路径权重和更小，显然当前边是可以删除的。

关键是，存在路径与这个边的权重相等时，该如何处理？
比赛的时候，我在纠结，会不会其他边也判断相等而把边删除，从而导致图最终不连通。

赛后思考了下，发现不存在这种情况。
因为与当前边权重相等的其他路径至少有两条边（不考虑重边），那么每条边的权重都小于当前边。

这意味着，大权重的边删除后，有其他小权重边来保证连通性。
这是一个递归的过程。
权重最小的边肯定不会删除。
故整个递归的正确性得以保证。

具体实现：

floyd 求任意两点之间的最短路（自身到自身的权重为无穷大）。
对于任意一条边 (x,y)，枚举所有顶点 z。
判断 x 先到 z 再到 y 是否可以代替当前边。
只要有一个顶点满足，当前边就可以删除。

F - Lottery

题意：有 N 个物品，每个物品有一个抽中的概率，所有物品概率之和为 100% 。
问抽 K 次（有K个物品），去重后恰好有 M 个的物品的概率是多少。

思路：

对于概率题，之前我从来没做出来过。
因为概率转化为逆元没去学过，总感觉很难。
这次看了题解，发现还挺简单的。

假设 N 个物品分别抽中 c(i) 次，和为 K，非 0 的个数为 M。

则答案的概率如下

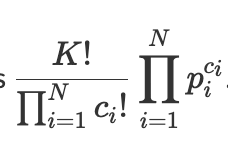
推导逻辑：

右半部分很容易理解，每个物品抽中 ci次，概率就是 pi^ci，即所有物品的概率相乘。

左半部是抽奖顺序的排列组合。
抽 K 个物品，总共有 K! 种排列。
物品 i 重复出现 c(i)次，所以多计算 c(i)! 次，需要除去。
每个物品独立，所以需要除去所有的 c(i)!。

上面的公式转化一下，发现每个物品是独立的，即 pi^ci / ci!。

每个物品独立，就可以使用动态规划来做这道题。
定义方程： f(n, m, k)
含义：前 n 个物品抽 k 次将得到 m 中不同的物品的概率。

转移方程：

f(n, m, k)
= 
 f(n-1, m  , k - 0) * p[n]^0 / 0!
+f(n-1, m-1, k - 1) * p[n]^1 / 1!
+f(n-1, m-1, k - 2) * p[n]^2 / 2!
+ ...
+f(n-1, m-1, k - k)  * p[n]^k / k!

注意事项1：非法数据，概率为0。
注意事项2：所有参数为0时，概率为 1。

G - Sqrt

题意：现在告诉你一个序列生成规则。
生成规则：如果序列最后一个元素值为 X，则可以在序列最后分别插入 [1,sqrt(X)] 这些值，并生成sqrt(X)个新的序列。
初始状态序列只有一个元素 X，问可以生成多少个不同的序列。

思路：

可以证明，每生成一轮，序列的最大值就降低为 sqrt(X)。
这个速度是反指数级别的，即 log 级别的。
对于 64 位整数，顶多 64 轮，最后一个元素就全部变成 1 了。
所以，输入任意一个整数，生成规则无限操作之后，最终生成的序列个数是稳定不变的。

怎么计算这个个数呢？

假设输入的 X 就是题意的最大值，即 X=9*10^18。
则第一轮可以生成 [1, 3*10^9] 为后缀的序列，数据范围还是很大。

假设 y=sqrt(3*10^9)。
分析之后发现，3*10^9 与 3*10^9-1 生成的序列的最后一位是一样的，都是 [1, y] 为后缀。

实际上，可以证明 [y^2, 3*10^9] 为后缀的序列，生成的序列最后一位都是一样的。
进而可以推理，[(y-1)^2, y^2-1] 为后缀的序列，生成的序列最后一位也一样的。 这样的区间可以倒推至 [1^2, 2^2-1]，即共 有 y 个。

y 大概为 5.x * 10^4，故我们分别计算出这 y 个区间的答案，相加即可。

假设 [1, y] 为后缀的序列最终稳定时，可以生成的序列个数分别都求出来了，为 f(x)，和为 sum(y)。

sum(y) = f(1) + f(2) + ... + f(y)

此时， [y^2, b] 为后缀的序列可以生成的序列个数就是 (b - y^2+1) * sum(y)。

如何求 5.x * 10^4 以内的所有 sum(y)。

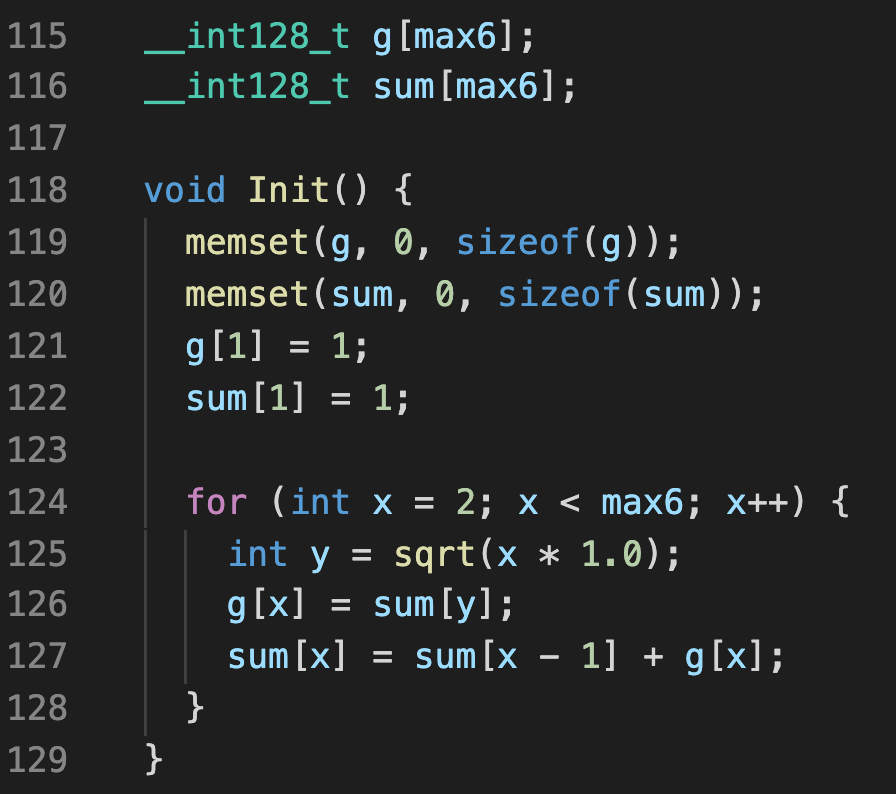
答案是预处理。
使用相同的原理求出 10^5 以内的所有 f(x)，累计求和既可以得到 sum(x)。

如果你归纳能力比较强的话，甚至可以发现 f(x) = sum(sqrt(x))。

所以，一层循环，就可以预处理出需要的数据了。

八、最后

这次比赛只做出前四题，第 G 题还剩 10 分钟时才读题，发现很简单，但是时间不够了。

不过这道题也有坑，大整数开方遇到精度问题，最终自己二分开方才通过。

E 题 和 F 题看了题解后发现也不难了。

最后一题扩展题，暂时还没看题解，这里就不介绍了。

加油，算法人。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code