leetcode 第 377 场比赛第四题

零、背景

上篇文章《leetcode 第 377 场算法比赛》提到，最后一题我使用O(1000^2)的复杂度超时了。

于是我参考了下其他人的代码，继续优化了下算法，分享下优化思路。

比赛代码:
https://github.com/tiankonguse/leetcode-solutions/tree/master/contest

一、题意

题意：给一个字符串映射到另外一个字符串的代价，问原始字符串是否可以替换为目标字符串，求最小代价。
规则：原始字符串到目标字符串的映射过程中，映射的子串之间不能有交集（相等除外）。

基本思路：

第一步：对映射的字符串进行hash处理，转化为数字之间的映射，并求全源最短路。
复杂度：O(200^3)

第二步：对原始字符串和目标字符串的所有子串进行预处理，求出对应的hash值。
复杂度：O(1000^2)

第三步：动态规划，枚举判断原始字符串后缀是否可以替换到目标字符串后缀。
方程：dp[i] = min(dp[j-1] + cost[fromHash][toHash] )
复杂度：O(1000^2)

二、全源最短路优化

全源最短路的复杂度最高。

由于点数最多200，边数最多只有 100 个，换其他最短路算法可以更优。

例如使用 SPFA+堆 单源最短路优化，复杂度只与边的个数有关。
复杂度降为：O(200^2)

三、hash 优化

我们计算了任意子串之间的 hash 值，空间复杂度和时间复杂度都是O(1000^2)。

其实可以只计算前缀的 hash，子串的 hash 可以通过两个前缀的差值来计算。

差值计算公式

f(l,r) = (f(0,r) - f(0,l-1) * base^(r-l+1)) % mod

前缀和base的幂都可以预处理，复杂度：O(1000)
计算子串hash的复杂度：O(1)

四、动态规划优化

默认动态规划是枚举所有长度，复杂度是 O(1000^2)

实际上，替换的点只有 100 个，说明可以替换的字符串长度最多最有 100 个。

故可以只枚举字符串长度集合。

复杂度：O(1000*100)

五、最后

优化后，各步骤的优化效果如下

第一步：求全源最短路 优化前：O(200^3) 优化后：O(200^2)

第二步：计算hash值
优化前：O(1000^2)
优化后：O(1000)

第三步：动态规划
优化前：O(1000^2)
优化后：O(1000*100)

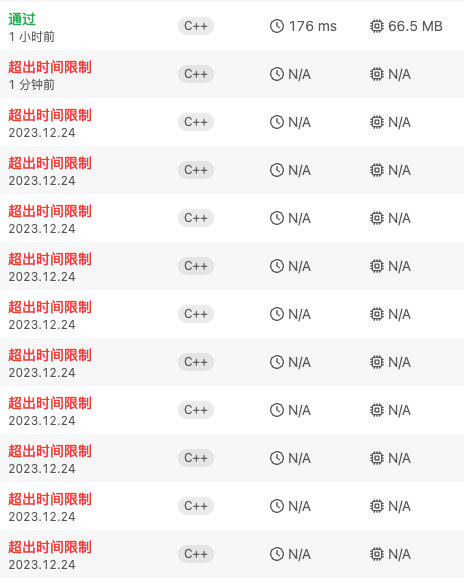
最终优化完，使用 176ms 通过了这道题。
优化前耗时至少 176ms，稍微加点常数，耗时就超过 2 秒了。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code