【算法讲解】字符串 hash

零、背景

Leetcode 算法比赛的题解中，我经常提到一个字符串 hash 这个算法。

那这个算法到底是什么意思呢？

今天详细讲解一下。

一、模运算

介绍 hash 算法之前，需要先介绍一下模运算的规则。

可重入: (a % p) % p = a % p
分配率: (a + b) % p = (a % p + b % p) % p
逆运算: (a * a^-1) % p = 1
除法: (a / b) % p = (a * b^-1)%p

当然，这篇文章暂时不展开介绍逆元。

一、基础场景

字符串 hash 基础的场景是大整数字符串,前缀 hash 值伪代码如下

int pre = 0;
for(int i=1;i<=n;i++){
    int vi = Val[i] - '0;
    pre = (pre * 10 + vi) % mod;
    preHash[i] = pre;
}

如果我们想要计算字符串区间val[3,5]的 hash 值，根据上面的算法，可以推论出

pre[5] = v1*10^4 + v2*10^3 + v3*10^2+ v4*10^1 + v5*10^0
preHash[5] = pre[5] % mod

pre[2] = v1*10^1 + v2*10^0
preHash[2] = pre[2] % mod


目标 = (v3*10^2 + v4*10^1 + v5*10^0) % mod
    = (pre[5] - pre[2] * 10^3) % mod
    = ((pre[5] % mod)  - (pre[2] * 10^3) % mod) % mod
    = (preHash[5] - prehash[2] * 10^3) % mod

从上面的公式中可以看到，把整个前缀当做一个大整数，较小的前缀需要进行左移，对齐最高位，从而可以求差，即可求出一个子串的 hash 值了。

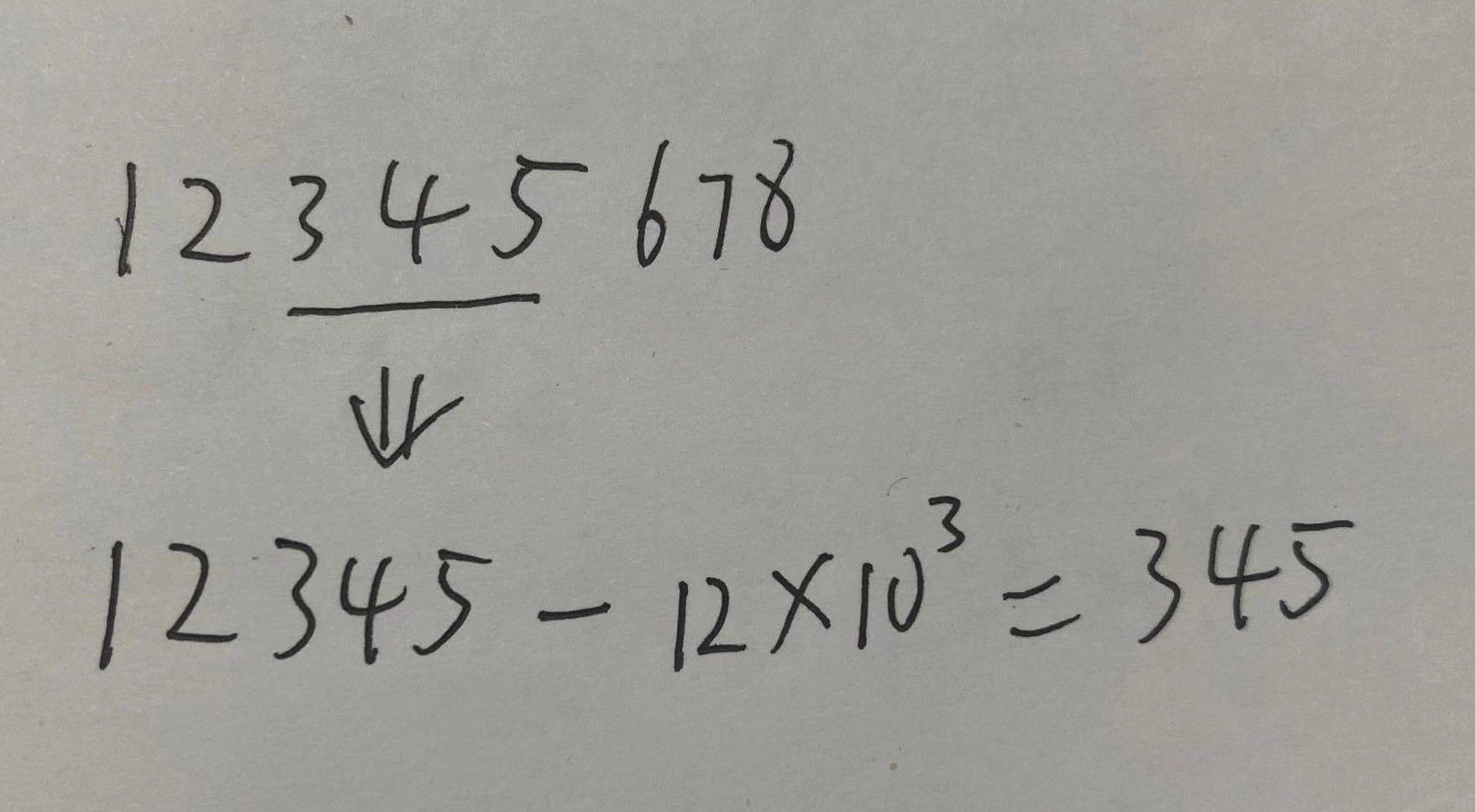
由此就可以写出区间子串的 hash 算法了。

ll RangeHash(int l, int r) { // [l, r]
  l--;  //(l, r]
  const int lr = r - l;
  const ll R = preHash[r];
  const ll L = preHash[l] * pow10[lr] % mod;
  return (R - L + mod) % mod;
}

二、通用场景

大整数的hash算法有一个缺陷，例如1和01的 hash 值相同。
所以大整数 hash 算法仅适用于题意明确说明是数字字符串的类型上。

对于英文字母字符串也一样，如果第一个字母 a 当做 0， a 和 aa的哈希值就会一样。

所以这个 hash 算法需要稍微进行调整，所有数字需要从 1 开始计数，这样就不会有重复值了。

对于纯数字，需要改成大于 10 的数字为幂底，例如选择 11。

int pre = 0;
for(int i=1;i<=n;i++){
    int vi = Val[i] - '0' + 1;
    pre = (pre * 11 + vi) % mod;
    preHash[i] = pre;
}

而对于纯小写字母，可以改成 27 为幂底，不过我习惯上选择质数为幂底，比例 29。

int pre = 0;
for(int i=1;i<=n;i++){
    int vi = Val[i] - 'a' + 1;
    pre = (pre * 29 + vi) % mod;
    preHash[i] = pre;
}

字符串的区间 hash 也可以轻松写出来了。

ll RangeHash(int l, int r) { // [l, r]
  l--;  //(l, r]
  const int lr = r - l;
  const ll R = preHash[r];
  const ll L = preHash[l] * pow29[lr] % mod;
  return (R - L + mod) % mod;
}

四、最后

好了，字符串 hash 和区间字符串 hash 算法已经介绍完了。

这里暂时没有介绍 hash 的逆元，因为当前的 hash 只需要使用减法和乘法即可得到对应的 hash 值。

后面有机会，在介绍带逆元的 hash 算法。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。