leetcode 第 378 场算法比赛

零、背景

2023 年 leetcode 最后一场周赛，第四题竟然是超级大模拟题，我敲代码速度慢，最后没敲完最后一题。

A：判断偶数个数是否大于2个。
B：预处理相同字符长度，二分求最优答案。
C：与第二题一模一样。
D：预处理前缀，两个线段分6种情况处理。

一、检查按位或是否存在尾随零

题意：给若干数字，判断偶数的个数是否大于2个。

思路：统计偶数的个数即可。

二、找出出现至少三次的最长特殊子字符串 I

题意：求至少出现 3 次的特殊子串，如果存在多个，返回长度最长的。
特殊子串：子串的字符都相等。

思路：特殊子串的字符都相等，所以不同字符之间就没啥关系。
假设存在一个长度为 A 的特殊子串，则长度为a的特殊子串，出现次数为 A-a+1。

我们可以预处理统计每个字符连续最长特殊子串出现的次数，遍历一遍即可求出指定长度特殊子串在原字符串中出现的次数。

vector<map<len, count>> stat;

之后二分答案，枚举每个字符是答案时，是否满足至少出现 3 个。

bool Check(int mid) {
  if (mid == 0) return true;
  for (auto& m : stat) {
    ll num = 0;
    for (auto [k, v] : m) {
      if (k < mid) continue;
      num += (k - mid + 1) * v;
      if (num >= 3) return true;
    }
  }
  return false;
}

三、找出出现至少三次的最长特殊子字符串 II

与第二题一模一样，相同代码提交两次即可。

四、回文串重新排列查询

题意：给一个偶数长度的字符串和若干查询，每个查询包含前后一半字符串的区间，问区间内的字符重排序，是否可以使得字符串变成回文串。

思路：题意有点抽象，简单理解就是字符串分为前后相等长度的前后缀。

问前缀有个区间的字符可以随意打乱，后缀有个区间的字符可以随意打乱，前后缀组成新的字符串是否是回文串。

回文转两个字符串

做这道题时，默认思路是直接按回文串处理，这个时候前后缀的下标是对称的。
其实还有另一种简洁的思路，即按两个字符串处理，这个时候两个下标就一样了。

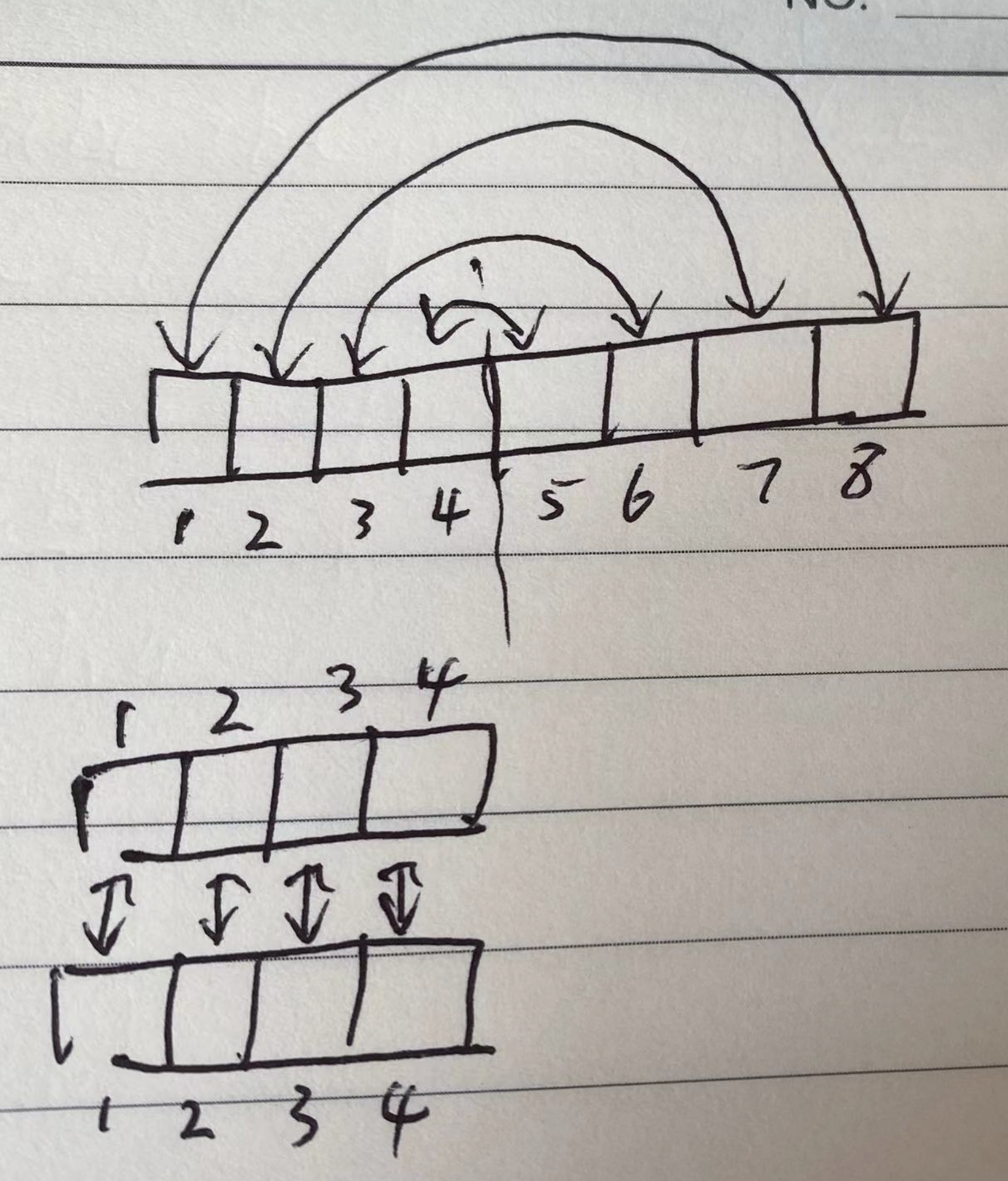
对于两个修改区间，共分为 6 种情况。

稍微一分析，可以发现，如果两个区间不区分先后的话，第1种和第6种等价，第2种和第5种等价，第3种和第4种等价。

所以，我们可以按两个修改区间的左边界进行判断，要求第一个区间的左边界比第二个小，这样就变成 3 种情况了。

if (range1.l <= range2.l) {
  ans.push_back(Solver(range1, range2, stat1, stat2));
} else {
  ans.push_back(Solver(range2, range1, stat2, stat1));
}

前后缀判断是否相等

首先，不管哪种情况，都需要先判断前后缀是否相等。
前后缀不相等，区间内如何修改都没有答案。

怎么判断呢？
可以预处理前后缀是否相等即可。

int minLeft = min(range1.l, range2.l);
int maxRight = max(range1.r, range2.r);
if (preCmp[minLeft - 1] != -1) {
  return false;  // 左边不对称
}
if (subCmp[maxRight + 1] != -1) {
  return false;  // 右边不对称
}

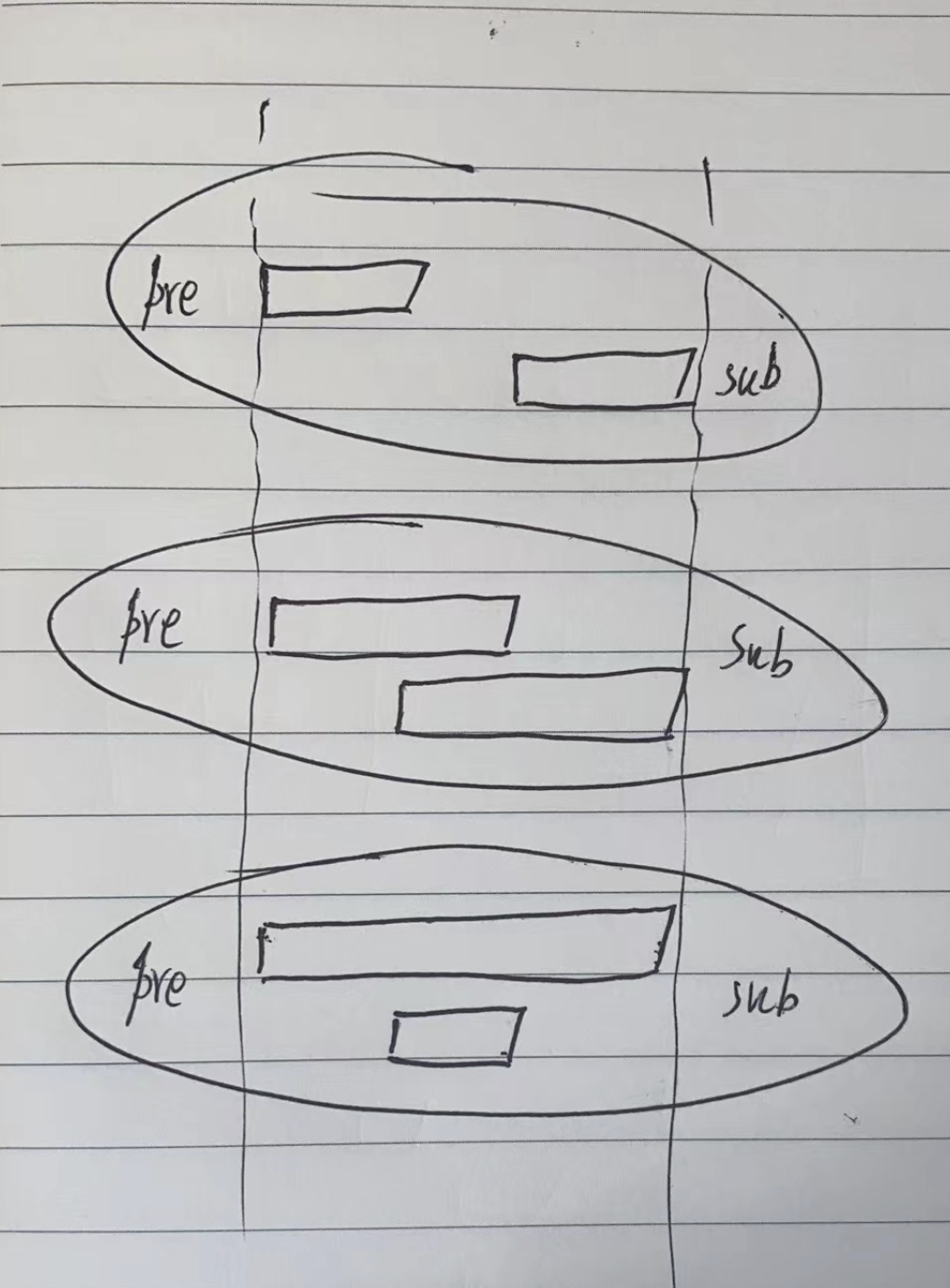
剩下的区间，就需要分情况判断了。

分为三种情况：

1）区间内，一个字符串不需要修改，另一个可以随意排列。对应两个区间有重叠时的差集。
2）区间内，两个字符串都可以随意排列。对应两个区间有重叠时的交集。
3）区间内，两个字符串都不能排列。对应两个区间没有重叠时，中间的空白区间。

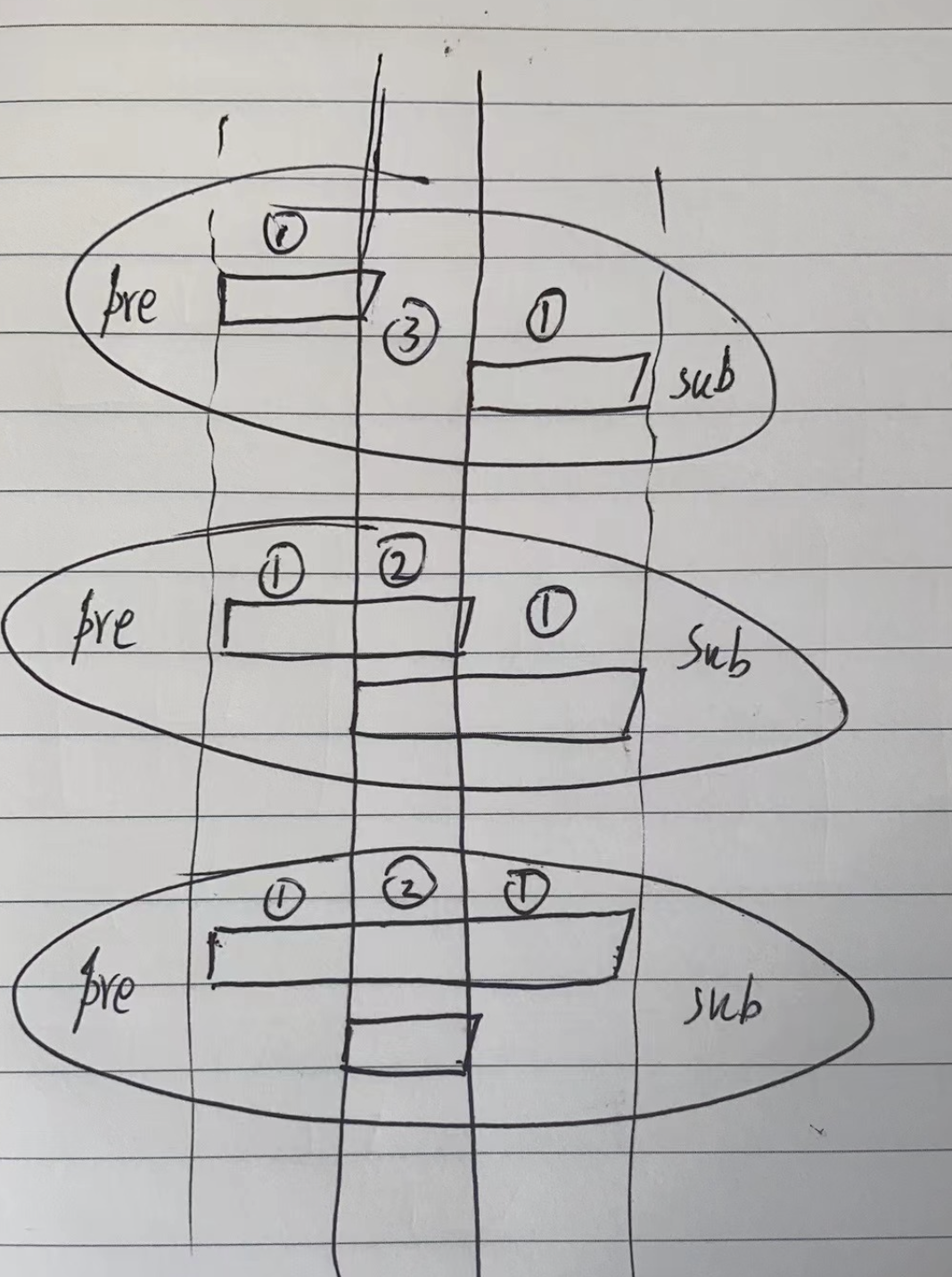
不过不断那种情况，处理之前，需要先统计区间内字符的个数。

vector<int> count1(26, 0);
vector<int> count2(26, 0);
for (int i = 0; i < 26; i++) {
  count1[i] = stat1.preStat[maxRight][i] - stat1.preStat[minLeft - 1][i];
  count2[i] = stat2.preStat[maxRight][i] - stat2.preStat[minLeft - 1][i];
}

另外，不管那种情况，都有情况1，即一个字符串要修改，另一个不需要修改。

以左半部为例，l1<l2，说明 s1 需要修改， s2 不需要修改。
两个统计数据都减去不需要修改的区间字符，判断剩余的统计是否还能保持一致。

// 步骤1：
if (l1 < l2) {  // 左半部对齐
  for (int i = 0; i < 26; i++) {  // [l1, l2-1]
    const int num2 = stat2.preStat[l2 - 1][i] - stat2.preStat[l1 - 1][i];
    count1[i] -= num2;
    count2[i] -= num2;
    if (count1[i] != count2[i]) {
      return false;
    }
  }
  l1 = l2;
}

左右的差集都处理后，就剩余中间的部分了。

一个是有重叠，一个是没重叠。

有重叠直接判断剩余的统计是否相等即可。

没有重叠时，比较复杂，需要判断区间子串是否相等

这个该怎么判断呢？

普通的预处理，需要预处理任意区间是否有答案，复杂度是O(n^2)。
这种情况，不管是空间复杂度还是时间复杂度，都超了。

一种优化是使用线段树或者树状数组来优化，复杂度O(n log(n))。

线段树的话，直接储存区间内是否相等即可。
树状数组的话，需要储存区间内不相等的个数或者相等的个数，前缀通过求差即可判断得到答案。

其实我们也可以通过预处理前缀来判断，复杂度O(n)。
预处理前缀时，记录最近一个不相等字符的位置。
区间查询时，通过最近一个不相等字符的位置和左边界比大小即可知道区间内是否有不相等的字符。

由此，所有情况都处理完成。

PS：有重叠区间和没重叠处理有差异，没有重叠的区间可以特殊处理一下。

五、最后

这次比赛第三题二分不算很难，最后一题是个大的模拟题了。
不仅要分情况处理，对于区间没有交集时，还需要判断区间子串是否相等，没想到前缀O(n)算法的话，只能上线段树或树状数组了。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code