leetcode 第 403 场算法比赛

零、背景

个人感觉这次比赛第三题更难，但没想到第三题过了这么多人。

A: 排序遍历。
B: 略。
C: 动态规划。
D: 枚举。

排名：117
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest/4/403

一、最小元素和最大元素的最小平均值

题意：给一个数组，每次选择一个最大值和最小值，问最后数组为空时，选择的元素对的最小平均值。

思路：排序，依次选择，保留最小和，最后除于二。

二、包含所有 1 的最小矩形面积 I

题意：给一个二维数组，求一个边与坐标轴垂直的最小矩阵的面积，使得这个矩阵恰好覆盖所有值为1的元素。

思路：上下左右求边界，然后公式计算出面积。

三、最大化子数组的总成本

题意：给一个数组，问怎么拆分子数组，才能使得所有子数组成本之和最大。
子数组成本：加上奇数位置元素，减去偶数位置元素。

思路：动态规划。

定义 F(a,b) 子数组 [a,b]的成本。
状态： f(a,b) 将子数组拆分之后的最大成本。

默认思路为暴力枚举，转移方程如下
f(0,n) = max(F(0,i) + f(i+1,n))
复杂度：O(n^2)

把数组画出来，分析每个位置的符号，可以发现某些子数组的符号是不变的，部分子数组的符号是翻转的。
故根据一个位置符号是否翻转，可以写出下面的状态和转移方程。

状态：f(n, sign) 第 n 个元素符号为 sign 时，后缀的最优答案。
方程：

f(n, +) = V[n] + max(f(n+1, +), f(n+1, -))
f(n, -) = -V[n] + f(n+1, +)

方程解释：
如果一个位置符号为正，则下个位置可以是新的子数字起始位置，也可以是当前的后缀，取最大值。
如果一个位置符号为负，则下个位置的符号必然为正。

复杂度：O(n)

四、包含所有 1 的最小矩形面积 II

题意：给一个 01 数组，问是否可以用三个不重叠的矩阵，覆盖所有值为1的位置。

思路：数据范围只有 30， 显然是要枚举的。

简单画图，可以发现只存在 6 种情况。

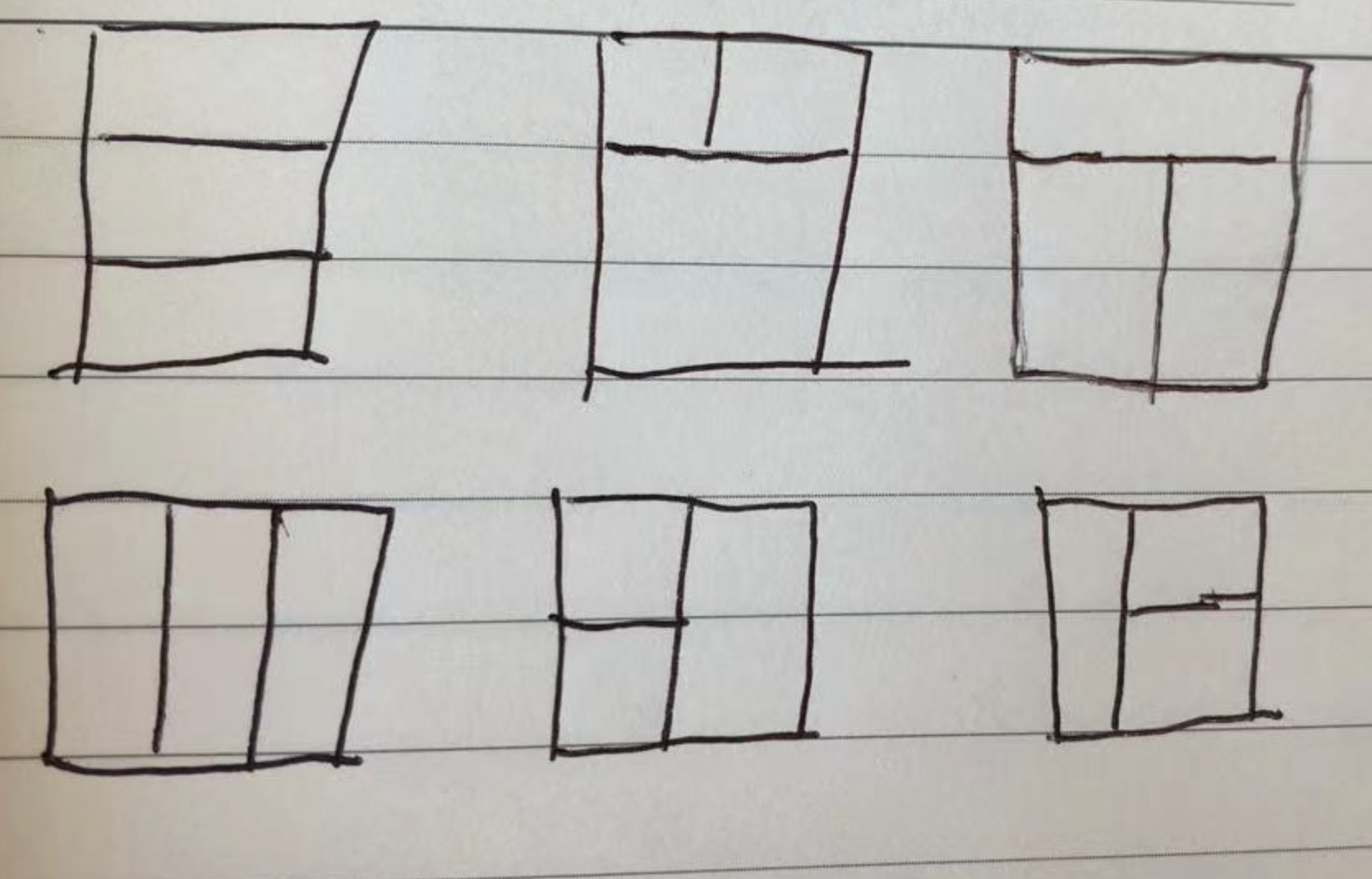
针对这 6 种情况，一种是一个个枚举，一个是 DFS 递归枚举。

我分析之后，发现如果旋转矩阵，则只有两种情况：两个行 或者 一个横一个竖。

所以我是通过旋转矩阵，然后枚举两种情况计算答案的。

五、最后

这次比赛最后一题是模拟题，而第三题则有点难度，不敢相信，竟然通过了 1266 人。

这次比赛第三题你是怎么想的，通过了吗？

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code