leetcode 第 404 场算法比赛

零、背景

个人感觉题目不难，我卡了好一会，竟然排名 36。

A: 枚举。
B: 动态规划。
C: 动态规划。
D: 动态规划+贪心。

排名：36
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest/4/404

一、三角形的最大高度

题意：给两个颜色的球。
要求摆一个三角形，每一行球的颜色相同，比上一行多一个球，不同行的球的颜色要求不同。
问最多可以摆多少行。

思路：枚举计算

显然，隔一行球的颜色相同。
假设可以摆 n 行，则可以根据奇偶性计算出奇偶行分别累计需要多少个球。
从小到大枚举答案，判断两个颜色的球是否满足奇偶行累计的球即可。

二、找出有效子序列的最大长度 I

题意：给一个数组，求一个子序列，使得子序列所有相邻位置元素之和的奇偶性相同。
求最长的子序列。

思路：动态规划。

显然，答案分两种情况：

情况1：所有元素奇偶性相同。
情况2：隔一个元素，奇偶性相同。

对于情况1，统计奇偶性个数即可。
对于情况2，奇偶性是交叉出现的，需要动态规划来做。

状态：dp(n, flag) 前 n 个元素，子序列最后位置奇偶性为 flag 的最长序列长度。
方程：

dp(n, flag) = dp(n-1, 1-flag) + 1;
dp(n, 1-flag) = dp(n-1, 1-flag);

优化：观察方程，可以发现当前状态只依赖上个状态，所以可以使用滚动数组。

方程：

dp(flag) = dp(1-flag) + 1;

三、找出有效子序列的最大长度 II

题意：给一个数组，求一个子序列，要求相邻子序列之和与 K 取模后都相等，求最长子序列。

思路：动态规划，与第二题相似，不优化即可。

显然，答案分两种情况：

情况1：所有元素取模后都相同。
情况2：隔一个元素，取模后值相同。

状态：dp(n, a, b) 前 n 个元素，子序列为 a,b交叉出现，最后位置取为 b 的最长序列长度。
方程：

dp(n, i, v) = dp(n-1, v, i) + 1;

优化：观察方程，可以发现当前状态只依赖上个状态，所以可以使用滚动数组。

方程：

dp(i, v) = dp(v, i) + 1;

同时可以发现，当 i 等于 v 时，就是第一种情况。
所以情况2的答案是覆盖情况1的，这里就不需要单独统计每个元素出现的次数了。

四、合并两棵树后的最小直径

题意：给两个树，问怎么使用一条边把两个树连起来，使得树的直径最小。

思路：动态规划+贪心。

树的直径定义为树中任意两个节点之间的最长路径长度。

根据这个定义，可以推导出一个几个推论。

推论1：假设非直径上的点 C 与直径 [A,B]的交点是为 D，则 CD 不大于 AD 和 BD。

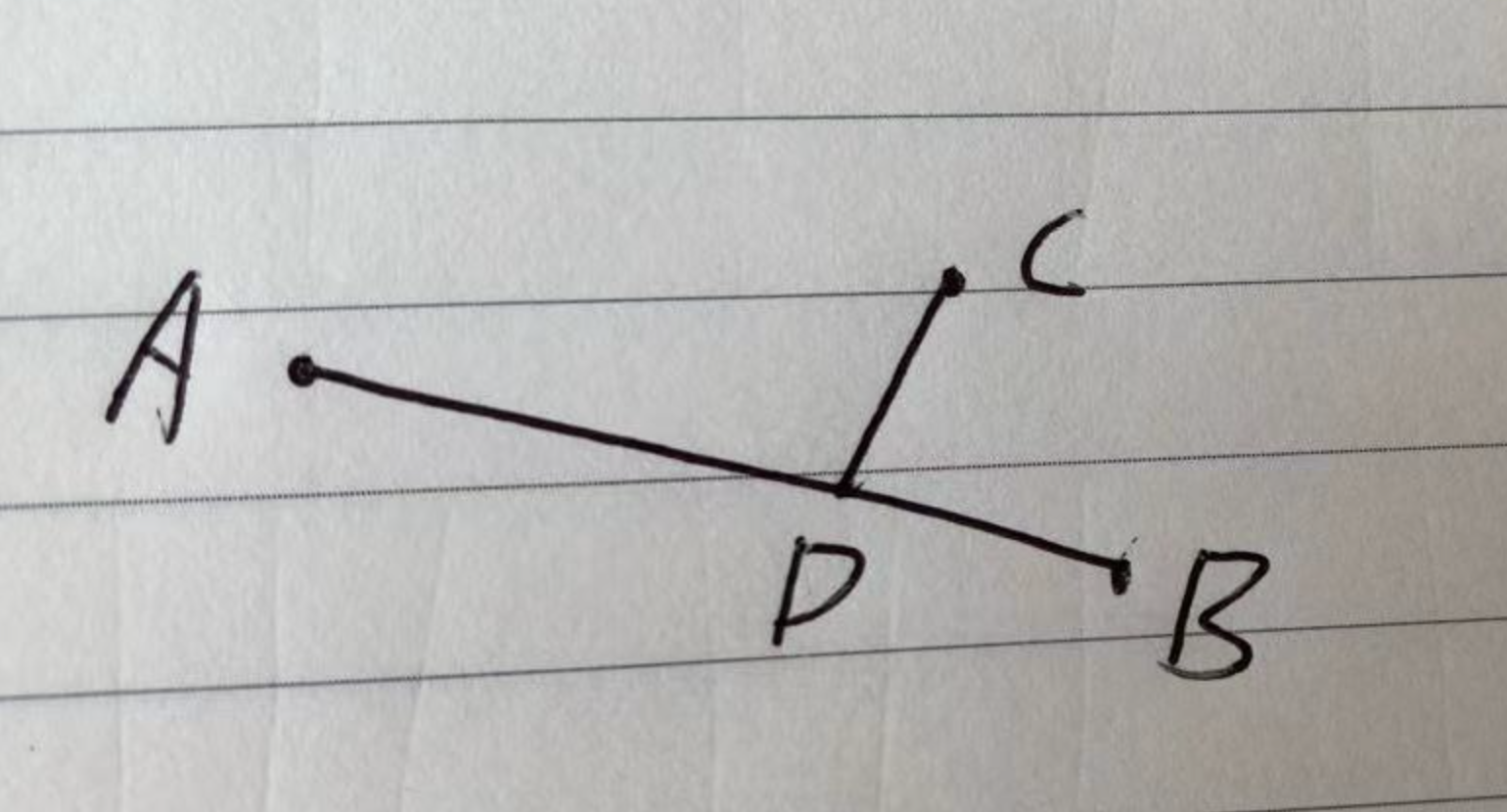
推论2：这道题两个树连接点必然在直径上。

假设不在直径上，不妨假设在 (D,C] 线段上，即为点 E。

另外假设 AD >= DB,根据推论1，可以推导出 AD>DB>=CD>=ED

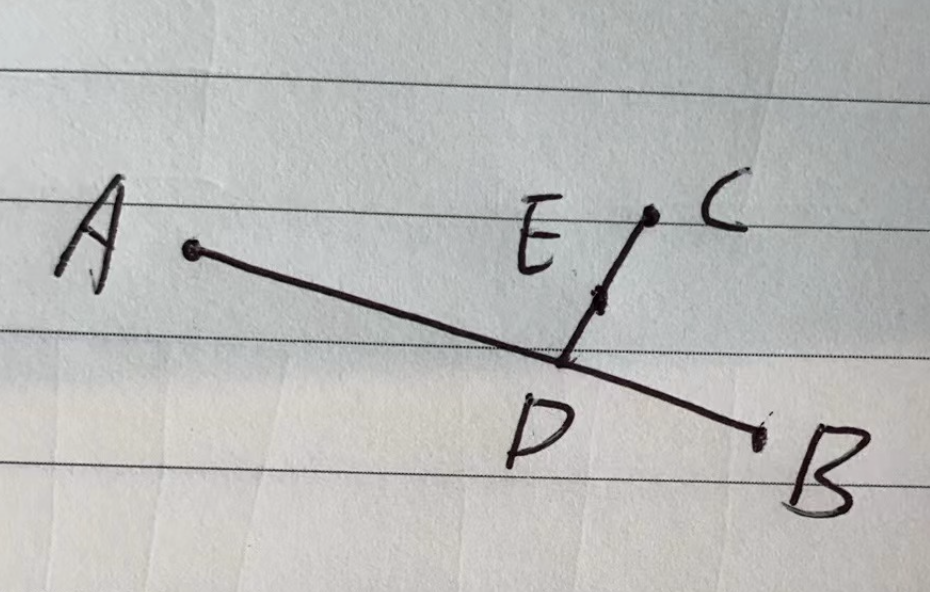
如果新形成的树的直径经过两个树，则直径在这个树的线段必然为 AD+ED。

可以证明，E 点越接近 D 点，这个树上的直径线段会越小。
即交点在直径上 D 上时，会比不在直径上更优。

推论3：连接在直径的中间最优。

推论2已经证明了两个树合并后的直径线段为 AD。
那显然 AD 越短越好。
由于 AD >= DB, 故故D 在直径的中间是最优的。

有了上面的推论，这道题得到这道题的算法。

1、求出两棵树的直径
2、合并后，树的直径可能不变，也可能变大。
变大时，直径由连接线和两个树的半径组成。

那如何求一棵树的直径呢？

思路1：贪心两边 dfs。
可以证明：任意选择一个点当做子树，深度最长路径的叶子节点肯定是直径的一个端点。
证明：见上面的推论1。
所以找到一个直径端点后，再dfs一边，就可以找到另外一个端点了。

思路2：树形DP。
递归求出每个子树经过子树根的最长路径。
经过根的最长路径：找到经过根的最长两条边，求和即可。

具体实现的时候，有很多优化，具体可以参考模版：

https://github.com/tiankonguse/leetcode-solutions/tree/master/doc/graph/tree

五、最后

这次比赛第一题其实也可以使用动态规划，这样的话四道题就都是动态规划了。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code