leetcode 第 443 场算法比赛
作者: | 更新日期:
最后两道都卡常数,没意思
本文首发于公众号:天空的代码世界,微信号:tiankonguse
零、背景
这次比赛都不难,但是最后两题都卡常数,优化项都是无意义的优化。
A: 贪心
B: 字符串 hash+二分+枚举回文串
C: 字符串 hash+二分+枚举回文串
D: 动态规划+线段树+滑动窗口预处理
排名:200+
代码地址: https://github.com/tiankonguse/leetcode-solutions/tree/master/contest
一、到达每个位置的最小费用
题意:有 n 个人站在一条直线上,起初你在最后位置,跳到指定位置有一个代价,现在问分别独立到达每个位置的最小代价。
说明:如果从当前位置往前跳,需要消耗代价,从前到后跳,不需要消耗代价。
思路:贪心
分析:对于一个目标位置,如果前面有更小的代价,则可以先消耗较小的代价跳到前面更小的代价,然后再免费跳到目标位置。
处理方法:从前到后枚举每个目标位置,记录前面的最小代价,然后计算当前位置的最小代价即可。
复杂度:O(n)
int minCost = cost[0];
for (int i = 0; i < n; i++) {
minCost = min(minCost, cost[i]);
ans[i] = minCost;
}
二、子字符串连接后的最长回文串 I
题意:给两个字符串,分别从两个字符串中取出一个子串,问两个子串按顺序拼接后是否是回文串,问最长回文串长度。
说明:按顺序拼接指的是第一个子串必须在左边,第二个子串必须在右边。
思路:字符串 hash+枚举进行回文判断
小技巧:对于回文串,可以在所有字符间插入一个特殊字符,这样就可以统一处理奇数和偶数长度的回文串。
又由于设计到字符串 hash,插入的特殊字符建议设置为 z 字符的下个字符。
最大答案除 2 即可。
void Fix(const string& s, string& ret) {
ret.clear();
ret.reserve(s.size() * 2 + 2);
ret.push_back('z' + 1);
for (auto c : s) {
ret.push_back(c);
ret.push_back('z' + 1);
}
}
对于目标答案,分两种情况:
1、中心对称位置在第一个字符串中,第二个子字符串是回文串一半的某个后缀,剩余的是第一个字符串的子串。
2、中心对称位置在第二个字符串中,第一个子字符串是回文串一半的某个前缀,剩余的是第二个字符串的子串。
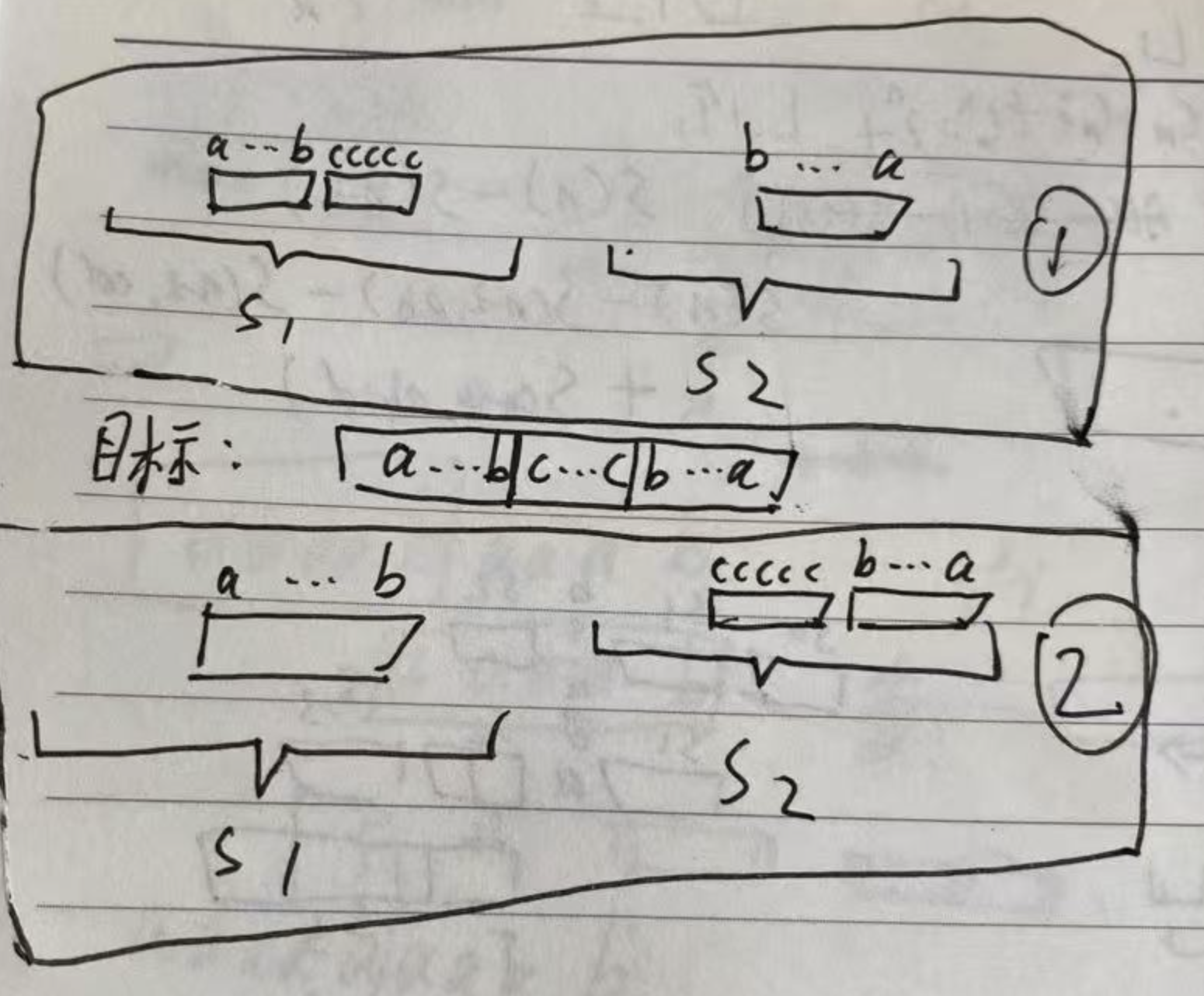
分情况之后,很容易想到枚举的方法。
假设中心位置在第一个字符串,枚举第一个字符串的中心与回文半径,即枚举c...c,然后找到最长的 a...b,使得 第二个字符串中存在子串 b..a。
复杂度分析:
枚举中心:O(n)
枚举半径:O(n)
枚举a..b:O(n)
判断是否存在:O(n^2)
如果不做任何优化,复杂度是O(n^5)。
显然,后面的三个操作都可以优化。
优化 1:判断是否存在,可以预处理出第二个子串所有子串逆序的 hash 值,这样就可以 O(1)判断是否存在了。
unordered_set<ll> H[max3]; // 各个长度子串的hash值
for (int i = 0; i < n; i++) {
ll pre = 0;
for (int j = i; j < n; j++) {
pre = (pre * BASE + (s[j] - 'a' + 1)) % mod;
H[j - i + 1].insert(pre);
}
}
优化 2:枚举a..b,可以发现这个其实可以单独预处理,求出位置a开始的与第二个字符串匹配的最长前缀,预处理后,就可以 O(1)得到最长的a..b了。
// 枚举中心位置
int ans = 0;
for (int i = 0; i < m; i++) { // 枚举中心位置
int l = i, r = i;
while (l >= 0 && r < m && t[l] == t[r]) {
int tmp = r - l + 1 + 2 * dp[r + 1];
ans = max(ans, tmp);
l--;
r++;
}
}
怎么预处理出位置a开始的与第二个字符串匹配的最长前缀呢?
简单写法是循环判断,即从小到大枚举位置a的所有前缀,判断在第二个字符串中是否存在。
复杂度:O(n^2)
fill_n(dp, m + 1, 0);
for (int i = 0; i < m; i++) {
ll pre = 0;
for (int j = i; j < m; j++) {
pre = (pre * BASE + (t[j] - 'a' + 1)) % mod1e7;
if (j - i + 1 <= n && H[j - i + 1].count(pre)) {
dp[i] = j - i + 1;
} else {
break;
}
}
}
考虑到这道题卡常数,可以使用二分优化。
复杂度:O(nlogn)
/ 预处理出 t 每个位置的可以回文匹配的最长子串
Init(t.c_str(), m);
fill_n(dp, m + 1, 0);
for (int i = 0; i < m; i++) {
int l = i, r = m; // [l, r)
while (l < r) {
int mid = (l + r) / 2;
if (mid - i + 1 <= n && H[mid - i + 1].count(HH(i, mid))) {
l = mid + 1;
} else {
r = mid;
}
}
dp[i] = l - i;
}
综合复杂度:O(n^2)
三、子字符串连接后的最长回文串 II
题意:与第二题一抹一眼,数据范围变成了 1000。
思路:第二题O(n^2)复杂度的算法超时了。
分析原因,插入特殊字符后,长度翻倍了,常数上就是翻了 4 倍。
通过各种其他优化后,我最终卡在了倒数第二组 case 上。
最终只好去掉特殊字符,分奇偶性来处理回文串。
代码变化不大,奇数中心代码如下:
int ans = 0;
for (int i = 0; i < m; i++) { // 枚举单点中心位置
int l = i;
int r = i;
ans = max(ans, dp[i] * 2); // 没有中心在这里一起计算了
while (l >= 0 && r < m && t[l] == t[r]) {
int tmp = r - l + 1 + 2 * dp[r + 1];
ans = max(ans, tmp); // 后缀回文匹配
l--;
r++;
}
}
偶数中心只是左右指针的变化。
for (int i = 0; i < m; i++) { // 枚举双点中心位置
int l = i;
int r = i + 1; // 与偶数中心唯一的差别
while (l >= 0 && r < m && t[l] == t[r]) {
int tmp = r - l + 1 + 2 * dp[r + 1];
if (tmp > ans) {
ans = max(ans, tmp); // 后缀回文匹配
}
l--;
r++;
}
}
就是这么神奇,不使用特殊字符后,就通过这道题了。
四、使 K 个子数组内元素相等的最少操作数
题意:给一个数组,可以选择 k 个长度都是 x 的不重叠子数组,问使得每个子数组的值相等的最小操作代价。
操作:每次可以选择一个数字加一或者减一。
思路:动态规划+线段树+二分。
k 只有15,线段是动态规划。
状态定义: f(n, k) 前 n 个数字满足 k 个的最优答案。
状态转移方程:分为选择与不选择
f(n,k) = max(f(n-1, k), f(n-x, k-1) + Cost(n))
// 前 n 个元素,拆分为 k 个长度为 x 且不重叠子数组,最小的代价
ll dfs(int n, int k) {
if (k == 0) return 0;
if (n < k * x) return __LONG_LONG_MAX__; // 无法拆分为 k 个长度为 x 的子数组
if (dp[n][k] != -1) return dp[n][k];
ll ans = __LONG_LONG_MAX__;
ans = min(ans, dfs(n - 1, k)); // 不选择最后一个元素, 可能没答案
ans = min(ans, dfs(n - x, k - 1) + cost[n]); // 选择最后一个元素,肯定存在答案
return dp[n][k] = ans;
}
现在问题转化为了,对于固定 x 个数字,加一或减一值相等的最小操作。
显然,中位数是最优答案(反证法)。
证明:显然,对于所有值域,操作代价是一个类似于抛物线的曲线,即最小值在中间,两边都是无限大。
假设不存在重复数字,中位数的值为 V 的答案是 Cost,中文数左边有 a 个数字,右边也是 a 个数字。
如果将目标修改为 V-1,则左边变成 a-1个数字,右边变成a+1个数字,答案是Cost+1。
同理,目标修改为V+1,则左边变成a+1个数字,右边变更a-1个数字,答案也是Cost+1。
左右答案都会变大,则说明中位数是一个最值,即最优值。
如果只需要计算一次中位数,排序即可。
但是这里需要找到所有下标为后缀的最后 x 个数字的中位数,这个就需要使用线段树来做了。
首先,需要对所有值域进行离散化,从而可以储存在线段树里。
map<ll, int> H;
vector<ll> h;
// 离散化
H.clear();
for (auto v : nums) {
H[v] = 0;
}
h.clear();
h.reserve(H.size() + 1);
for (auto& [kk, vv] : H) {
h.push_back(kk);
vv = h.size();
}
线段树储存值的个数,从而可以滑动窗口维护线段树,使用二分查找中位数。
// 滑动窗口计算 cost 的值
cost.resize(n + 1, -1);
for (int i = 1; i <= n; i++) {
segTreeCount.Update(H[nums[i - 1]], 1);
segTreeSum.Update(H[nums[i - 1]], nums[i - 1]);
if (i < x) {
continue;
}
dp2[i] = Search();
segTreeCount.Update(H[nums[i - x]], -1);
segTreeSum.Update(H[nums[i - x]], -nums[i - x]);
}
二分找到中位数后,还需要计算代价,这个可以通过区间和的加加减减来计算出来。
ll Search() {
// 如果 x 是 奇数,则中位数是 x/2+1
// 如果 x 是 偶数,则中位数是 x/2
int midX = (x + 1) / 2; // 等价与 (x + 1) / 2
int l = 1, r = H.size();
while (l < r) {
int m = (l + r) >> 1;
if (segTreeCount.QuerySum(1, m) >= midX) {
r = m;
} else {
l = m + 1;
}
}
ll minV = h[l - 1];
ll lessNum = segTreeCount.QuerySum(1, l);
ll lessSum = segTreeSum.QuerySum(1, l);
ll moreNum = segTreeCount.QuerySum(l, H.size());
ll moreSum = segTreeSum.QuerySum(l, H.size());
return moreSum - moreNum * minV + minV * lessNum - lessSum;
}
分析下各个步骤的复杂度:
离散化:O(n log(n))
滑动窗口:O(n log(n) log(n))
动态规划:O(n k)
可惜这个代码超时了,我做了各种优化,依旧超时。
最后把离散化的 map<ll, int> H; 修改成 unordered_map<ll, int> H 后才通过。
此时分析下复杂度:
离散化(含排序):O(n log(n))
滑动窗口:O(n log(n) log(n))
动态规划:O(n k)
每个步骤的复杂度都一样,但是这样就通过了。
五、最后
最近了解到 leetcode 的排名机制是看最优一题的通过时间。
所以我就直接做最后一题了,结果被卡住了,悲剧。
但是 leetcode 这次后两次的卡常数就没意思了。
《完》
-EOF-
本文公众号:天空的代码世界
个人微信号: tiankonguse
公众号 ID: tiankonguse-code
本文首发于公众号:天空的代码世界,微信号:tiankonguse
如果你想留言,可以在微信里面关注公众号进行留言。
