leetcode 第 444 场算法比赛

零、背景

这次比赛其实也不难，不过代码量比较多大，做3道题就可以进入前百名，做四道题可以进入前20名，不过我没参加比赛。

A: 模拟，暴力
B: 队列+二分
C: 动态规划
D: 模拟，维护正反索引

排名：无
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest

一、移除最小数对使数组有序 I

题意：给一个数组，如果不满足非递减，则选择相邻和最小的二元素合并为一个元素，直到满足非递减为止。
问需要合并多少次。

思路：数据范围不大，按题意暴力模拟即可。
逻辑：每次判断是否满足非递减，如果不满足，则循环找到相邻的最小对，合并为一个元素。
复杂度：O(n^2)

二、设计路由器

题意：要求实现一个固定内存大小的路由器，支持下面几个操作：
1）初始化：至多可以储存 memoryLimit 个数据包
2）数据包入队：将三元组(A,B,T)加入到路由器，如果已存在则不加入，如果内存满了删除最旧的数据包。
3）数据包出队：删除最旧的数据包，并返回数据包的三元组(A,B,T)。
4）目标查询：查询路由器中目的地是 B 的时间范围在 时间 T1 到 T2 之间的数据包个数。

特征：
-）总操作次数 10^5
-）数据包入队的时间严格非递减。

思路：构造题。

1）维护一个队列，储存数据包的三元组(A,B,T)。
2）维护一个三元组的哈希表，判断数据包是否存在。
3）对于每个目标 B，单独储存有序的时间线，可以使用哈希表储存hash<B, vector<T>>。
4）对于每个目标 B，维护一个时间线的游标，代表时间线里未删除的第一个数据包。

巧妙之处：不进行实际删除，只维护一个游标，从而可以保证删除的复杂度不会退化到 O(n)

操作如下：

1）入队
1.1）先判断是否存在，如果存在则不加入，返回 false。
1.2）判断内存是否满了，如果满了，调用出队操作，进行出队。
1.3）将数据包加入到队列中，加入三元组哈希表，加入 B 对应的时间线的结尾。
2）出队
2.1）判断队列是否为空，如果为空则返回空数组。
2.2）删除队列的第一个数据包
2.3）删除三元组哈希表
2.4）目标 B 的时间线的游标加 1。
2.5）返回三元组。
3）查询
3.1）判断 B 是否存在，不存在则返回 0
3.2）二分查找时间线，找到 T1 和 T2+1 的位置，返回位置的差值。

空间复杂度：O(n)
时间复杂度：O(n log(n))

三、最大化交错和为 K 的子序列乘积

题意：给一个数组，求一个交错和为K 乘积不大于 limit 的乘积最大的子序列。
交错和定义：下标从0开始，偶数求和，奇数求差。

思路：典型的动态规划。

状态定义：f(flag, N, K, limit) 前 N 个元素，最后一个元素奇偶性为 flag，和为 K，乘积不大于 limit 的最优答案。
状态转移方程：

f(flag, N, K, limit) = max(
  f(flag, N-1, K, limit),  // 不选择
  f(flag^1, N-1, K+v*sign, limit/v) * v // 选择
)

特殊情况1：对于乘法，递归出口有效值需要是 1。但是初始值 1 与 答案为 1 的情况无法区分。
所以状态需要储存两个值，一个是答案，一个是选择的个数。
即 f(flag, N, K, limit) = {ans, count}。

特殊情况2：由于存在除 0,所以 0 需要特殊判断，然后过滤掉 0。
这个特殊处理是一个类似的动态规划。

状态定义：f0(flag, N, K) 前 N 个元素，最后一个元素奇偶性为 flag，和为 K 时 0 的最多个数。
状态转移方程也类似：

f0(flag, N, K) = max(
  f0(flag, N-1, K),  // 不选择
  f0(flag^1, N-1, K+v*sign) + (v==0) // 选择
)

理论空间复杂度：O(2*N*K*limit)。
N 为 150
K 为 2*10^5
limit 为 5000
合起来复杂度是 O(10^11)，理论上储存不下，也会超时。

实际复杂度并没有这么大。
首先是 K 的数据范围，有效的范围是 [-12*150 ,+12*150]，上限个数为 3600个，加减交替，实际会更少。
也就是 K 不在这个范围的，都不可能存在答案。

但是实际分析递归树，可以发现有效状态非常少，递归空间收敛非常快的。

例子：对于最后一个 n，只有两个状态 f(0,n,k,limit) 和 f(1,n,k,limit)。
如果不选择，则对应状态 f(0,n-1,k,limit) 和 f(1,n-1,k,limit)。.
如果选择，则对应状态 f(0,n-1,k+v*sign,limit/v) 和 f(1,n-1,k+v*sign,limit/v)。

第一层有 2 个状态，第二层有 4 个状态，每层状态翻倍。
但是 limit 每次是除法，越往下越小， 5000 顶多选择 13 次左右大于 2 的值。
这样均摊下来，复杂度预估在 10^6 左右。

使用递归写法不会超时，我的代码耗时 2831 ms 通过。
状态储存的话，可以使用 tuple 作为哈希表的 key。

map<tuple<int, int, int, int>, pair<int, int>> dp;

四、移除最小数对使数组有序 II

题意：与第一题一样，不过数据范围变大了。

思路：分析模拟过程，每次操作的位置起始是确定的。
故可以构造一个数据结构，来快速找到要操作的位置进行操作即可。

数据结构1：有序字典表 map<index, value>：储存每个下标的值。
逻辑：中间合并后，中间就会有空洞，使用有序集合可以快速找到前一个与后一个的下标和值。

数据结构2：二元组之和与下标的有序集合 map<pair<sum, leftIndex>, rightIndex>。
逻辑：每次需要找到最小和，相同时候需要找到最小的下标，故二元组之和与左下标当做有序集合的 key，右下标当做 value。

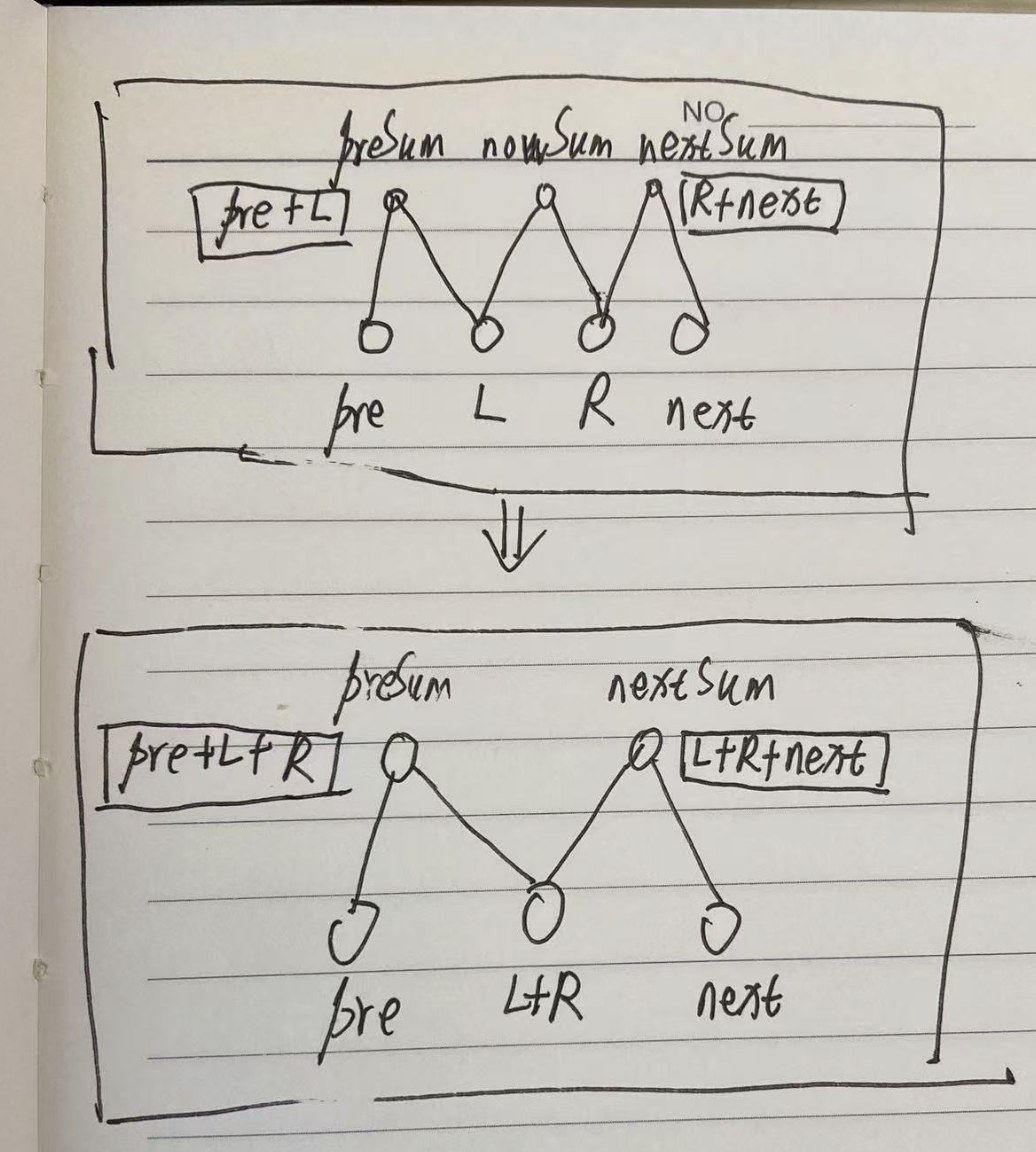
如上图，如果你画出元素的序列和和关系，就大概知道怎么维护这两个数据结构了。

每次合并时，对于数据结构1，需要删除一个元素，删除元素的值加到剩余的元素上。
另外，我们需要找到前一个元素和后一个元素，更新数据结构2，需要注意的是需要指向合并后的哪个元素位置。

前一个元素可以使用 lower_bound(L) 来找到。
后一个元素可以使用 upper_bound(R) 来找到。
然后按照两个数据结构的关系，进行增删改查。

稍等，我们怎么知道数组是否有序呢？

所以这里还需要数据结构3：相邻元素的逆序对个数。
每次进行合并时，也更新这个相邻元素逆序对个数即可。

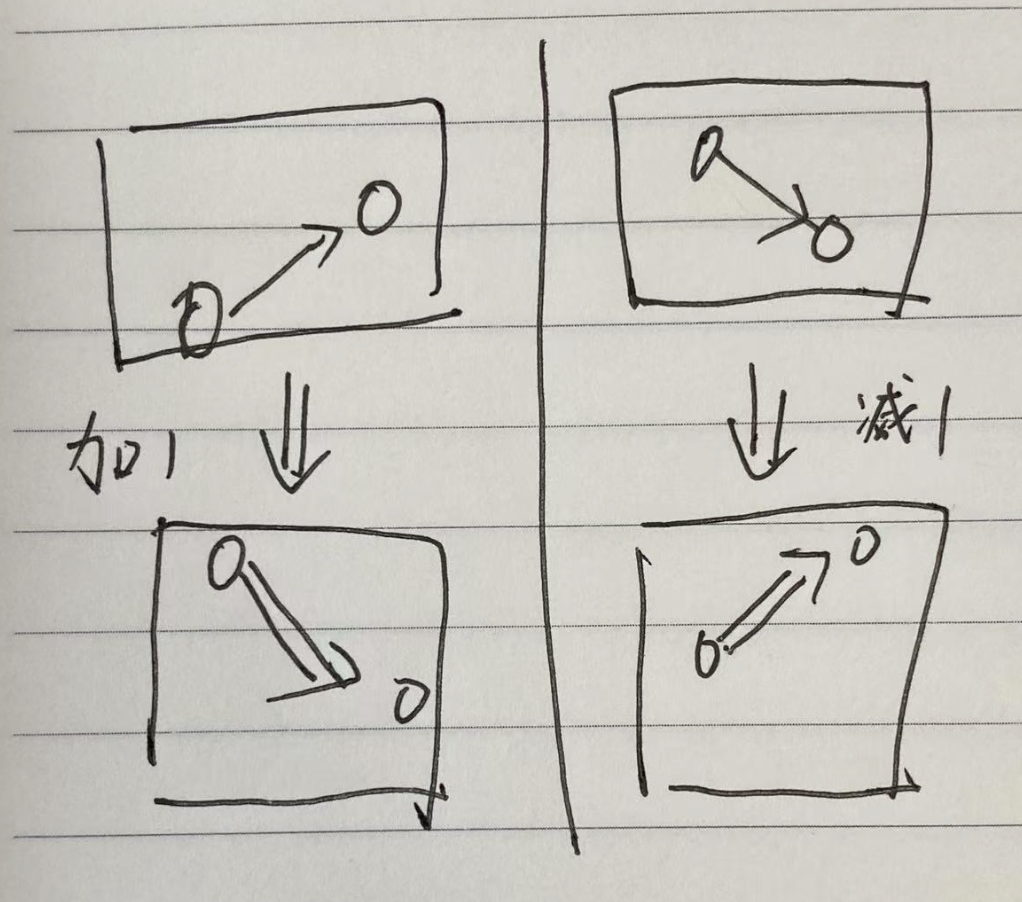
这里贴一下前一个元素的处理代码，后一个是类似的。

const auto itMin = sumToRightIndex.begin();
const auto [oldSum, leftIndex] = itMin->first;
const int rightIndex = itMin->second;
const ll leftOldVal = indexToValue[leftIndex];
const ll rightOldVal = indexToValue[rightIndex];

// 最小二元组进行合并操作
sumToRightIndex.erase(make_pair(leftOldVal + rightOldVal, leftIndex)); // 先删除
if (leftOldVal > rightOldVal) {
  lowerNum--;
}
indexToValue.erase(rightIndex);
indexToValue[leftIndex] = oldSum;

// 前一个二元组更新
if (auto it = indexToValue.lower_bound(leftIndex); it != indexToValue.begin()) {
  it--;  // 上一个
  const int preIndex = it->first;
  const ll preValue = it->second;
  if (preValue > leftOldVal && preValue <= oldSum) {
    lowerNum--;
  } else if (preValue <= leftOldVal && preValue > oldSum) {
    lowerNum++;
  }
  sumToRightIndex.erase(make_pair(preValue + leftOldVal, preIndex));
  sumToRightIndex[make_pair(preValue + oldSum, preIndex)] = leftIndex;
}

// 后一个二元组更新
if (auto it = indexToValue.upper_bound(rightIndex); it != indexToValue.end()) {
}

五、最后

这次比赛题目没有非常难，但是从第二题开始代码量就都比较大。
第二题大模拟、第三题需要写两个动态规划，第四题还是大模拟。
leetcode 这次题目出的非常不合理，一般比赛只应该出一个大模拟的，毕竟模拟代码量很大，需要很多时间来调试的。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号： tiankonguse
公众号 ID： tiankonguse-code