leetcode 第 461 场算法比赛

零、背景

这次比赛期间我在厦门旅游，工作也一直比较忙，所以拖更了一周。
周六天气比较热没出门，于是做了下题并补了题解。

A: 模拟
B: 贪心+动态规划
C: 二分
D: 枚举

排名：无
代码地址： https://github.com/tiankonguse/leetcode-solutions

一、三段式数组 I

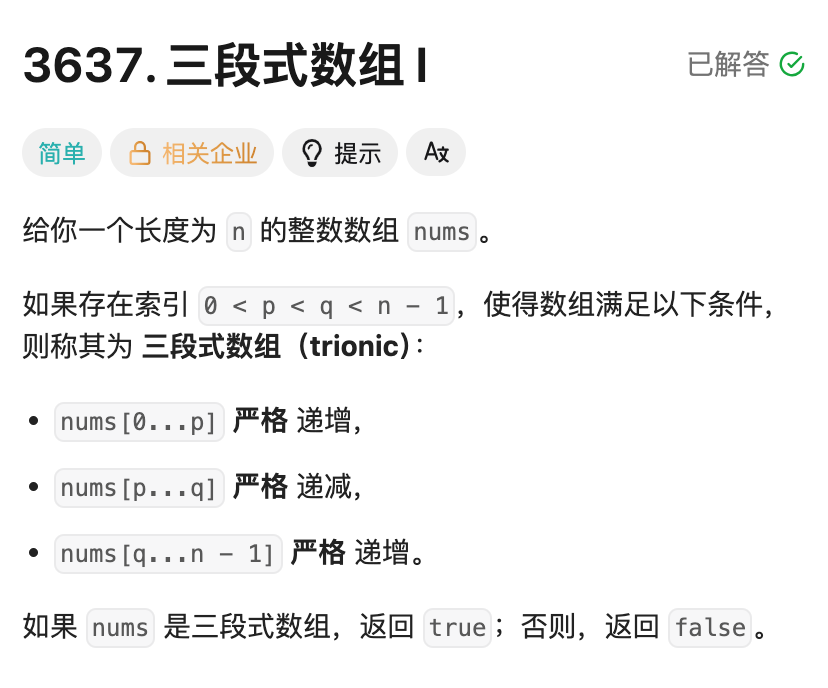
题意：给一个数组，问是否可以找个两个位置 p 和 q，使得 [0,p] 是升序，[p,q]是降序，[q,n-1]是升序。

思路：模拟

先扫描数组，得到所有的边界位置。

// 第一步：计算出有序性的分割线
vector<int> nodes;
nodes.reserve(n);
int dir = 0;  // 0: 未知, 1: 上升, -1: 下降
nodes.push_back(0);
for (int i = 1; i < n; i++) {
  int newDir = 0;
  if (nums[i - 1] < nums[i]) {
    newDir = 1;
  } else if (nums[i - 1] > nums[i]) {
    newDir = -1;
  }
  if (dir != 0 && dir == newDir) {
    nodes.pop_back();
  }
  nodes.push_back(i);  // 相等的情况,当做分割线
  dir = newDir;
}

对于边界位置，预期应恰好有 4 个，且三个线段满足先升序，再降序，再升序

const int m = nodes.size();
if (m != 4) return false;
const int l = nodes[0];
const int p = nodes[1];  // 上升的结束点
const int q = nodes[2];  // 下降的结束点
const int r = nodes[3];  // 上升的结束点
return nums[l] < nums[p] && nums[p] > nums[q] && nums[q] < nums[r];

二、平衡装运的最大数量

题意：给一个数组，问最多可以拆分多少个不重叠子数组，使得子数组的最后一个数字严格小于子数组的最大值。

思路：贪心

子数组的最后一个数字严格小于子数组的最大值，等价于子数组的最后一个数字不是最大值。

假设子数组的右边界确定后，左边界有很多，由于允许某些数组不选择，显然子数组越短越好，即左边界越往右越好。
符合要求的最短的子数组，左边界是第一个大于右边界的位置。

故可以维护一个单调栈，预处理计算出所有位置为右边界时的最优左边界。

vector<int> preMax(n, -1);
vector<int> sta;
sta.reserve(n);
for (int i = 0; i < n; i++) {
  while (!sta.empty() && weight[sta.back()] <= weight[i]) {
    sta.pop_back();
  }
  preMax[i] = sta.empty() ? -1 : sta.back();
  sta.push_back(i);
}

左边界确定了，问题就转化为了最多线段不重叠的选择问题了，是一个典型的动态规划。

状态定义：f(i) 前i个数字的最大选择数量。
状态转移方程：f(i) = max(f(i-1), f(preMax[i]-1)+1)
方程解释：最后一个数字分为选择与不选择

int ans = 0;
vector<int> dp(n, 0);
for (int i = 1; i < n; i++) {
  dp[i] = dp[i - 1];
  if (preMax[i] != -1) {
    if (preMax[i] > 0) {
      dp[i] = max(dp[i], dp[preMax[i] - 1] + 1);
    } else {
      dp[i] = max(dp[i], 1);
    }
  }
}
return dp[n - 1];

三、变为活跃状态的最小时间

题意：给一个字符串，每个时间点修改字符串指定位置为特殊字符。问最少需要多少时间，可以使得含有特殊字符的子字符串个数至少为 k 个。

思路：二分

二分时间，判断是否满足条件。

int l = 0, r = n;
while (l < r) {
  int mid = (l + r) / 2;
  if (Check(mid)) {
    r = mid;
  } else {
    l = mid + 1;
  }
}
if (l == n) return -1;
return l;

检查时，暴力检查每个位置作为左边界时，有多少个子字符串满足条件，并累计求和。
显然，确定左边界后，第一个满足条件的位置是左边界右边的第一个特殊字符的位置，之后的也都满足。
复杂度：O(n log(n) log(n))

set<int> S;
auto Check = [&](const int mid) -> bool {
  S.clear();
  for (int i = 0; i <= mid; i++) {
    S.insert(order[i]);
  }
  ll ans = 0;
  for (int i = 0; i < n; i++) {
    auto it = S.lower_bound(i);
    if (it != S.end()) {
      ans += n - *it;
    }
  }
  return ans >= k;
};

优化1：S 集合中小于 i 的元素都无效，故可以实时删除小于 i 的元素。此时右边界就是 S 集合中的第一个元素，复杂度不变。
优化2：不使用集合，直接使用数组，排序后与集合等价，使用游标代替删除，复杂度不变。
优化3：数据范围[0,n-1]，使用计数排序，复杂度可以降低到 O(n log(n))

优化4：递推。

分析每个时刻标记一个位置时新增的满足条件的子字符串，与之前与之后相邻的已经标记的位置相关。

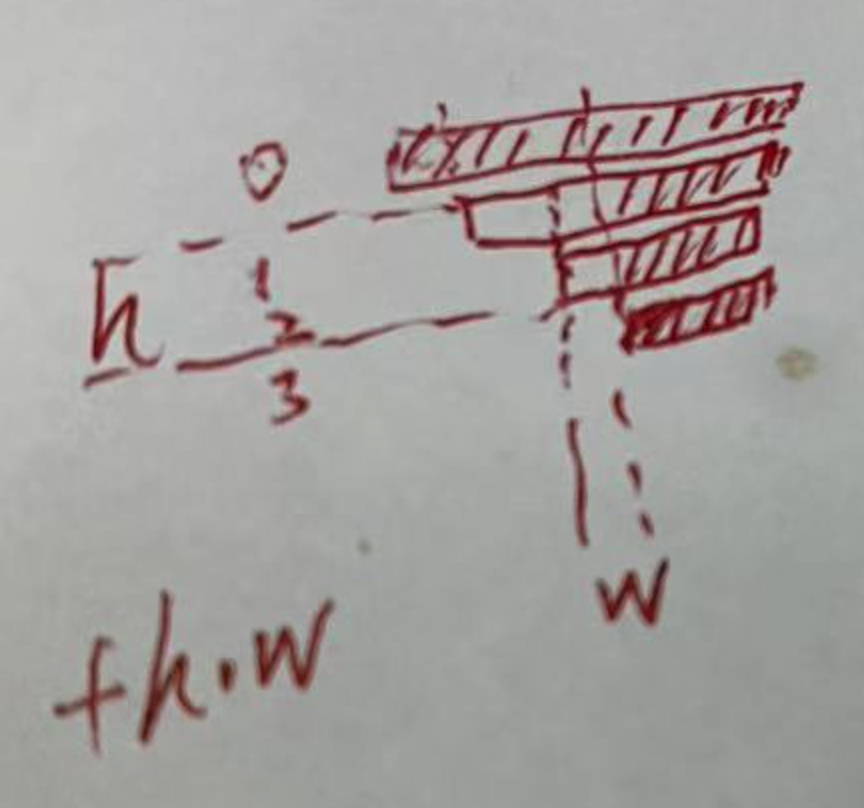
如下图，行号代表子串的左边界位置，右边界依次递增到最后。
标记某个位置为特殊字符后，这个位置为左边界的所有子字符串都满足条件，另外左边界小于这个位置的子串也都满足答案，即新增的满足条件的子串可以组成一个矩阵。

假设位置0和位置3已经被标记，满足要求的子串为图中阴影部分。
此时新增位置2，则位置2为左边界的满足条件的子串个数为 W,即下一个标记位置减去当前位置。
位置2还会影响小于位置2的子串，影响的边界个数记为 H，即当前位置减去前一个标记位置。
两个相乘就是这次新增的满足条件的子串个数。

ll ans = 0;
set<int> S;
for (int t = 0; t < n; t++) {
  const int i = order[t];
  auto it = S.lower_bound(i);  // 不存在相等值
  ll w = n - i;
  if (it != S.end()) {
    w = *it - i;
  }
  ll h = i + 1;
  if (it != S.begin()) {
    --it;
    h = i - *it;
  }
  ans += w * h;
  if (ans >= k) {
    return t;
  }
  S.insert(i);
}

四、三段式数组 II

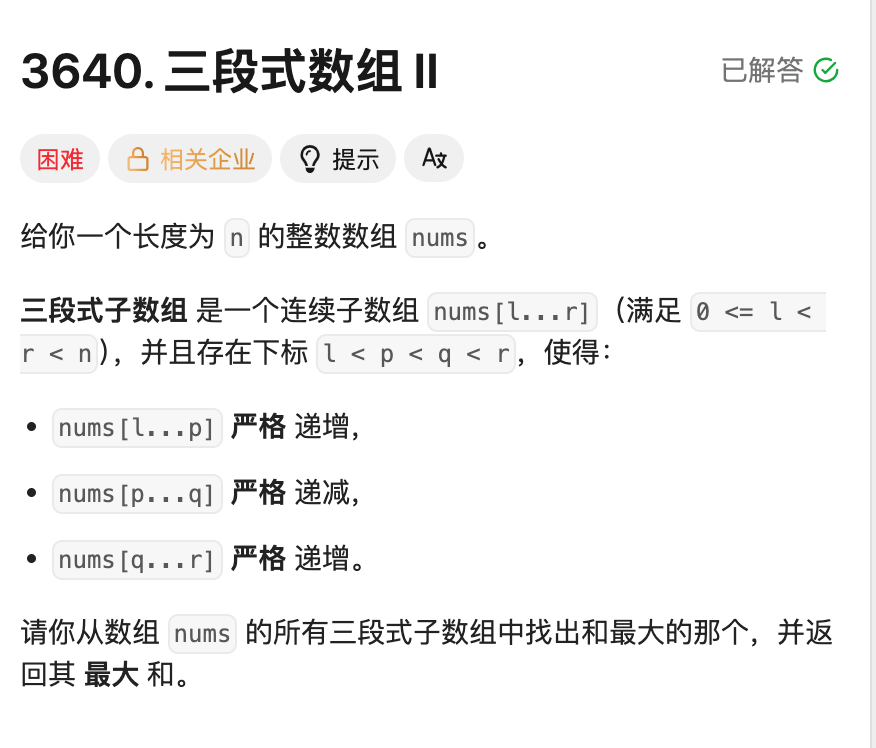
题意：给一个数组，需要找到一个三段式子数组，满足先严格升序再严格降序，后严格升序。
如果存在多个，返回子数组和最小的。

思路：枚举

与第一题一样，预处理出所有分割点。

然后枚举分割点，找到满足要求的三段式子数组。

可以发现，中间那一段和是固定的，左右两边的段可以缩短，所以需要分别找到左右端的最大和。
直接暴力搜索分别求最大和即可。
复杂度：O(n)

ll ans = -INFL;
const int m = nodes.size();
for (int i = 0; i + 3 < m; i++) {
  const int l = nodes[i];
  const int p = nodes[i + 1];  // 上升的结束点
  const int q = nodes[i + 2];  // 下降的结束点
  const int r = nodes[i + 3];  // 上升的结束点
  if (nums[l] < nums[p] && nums[p] > nums[q] && nums[q] < nums[r]) {
    // 计算三段的和
    ll sum = 0;
    ll tmp1 = nums[p - 1];
    ll sum1 = tmp1;
    for (int j = p - 2; j >= l; j--) {
      tmp1 += nums[j];
      sum1 = max(sum1, tmp1);
    }

    ll sum2 = 0;
    for (int j = p; j <= q; j++) {
      sum2 += nums[j];
    }
    
    ll tmp3 = nums[q + 1];
    ll sum3 = tmp3;
    for (int j = q + 2; j <= r; j++) {
      tmp3 += nums[j];
      sum3 = max(sum3, tmp3);
    }
    ans = max(ans, sum1 + sum2 + sum3);
  }
}

五、最后

这次比赛整体难度不大。

第一题按题意模拟，第二题是简单的动态规划，第三题用二分，第四题是枚举模拟。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号： tiankonguse
公众号 ID： tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。