CSP-S 2021 编程算法比赛

零、背景

最近我计划研究 CSP-J 与 CSP-S 的比赛题目，之前已经完成了 7 场比赛的题解，今天将分享 2021 年 CSP-S 第二轮编程算法比赛的详细题解。

A: 二分+线段树
B: 语法解析+动态规划
C: 贪心搜索
D: 对偶图+最短路+环形DP

代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/other/CSP-S/

比赛题目分类与题解
CSP-J 2024 题解 A:扑克牌入门 B: 地图探险普及− C: 小木棍普及/提高− D: 接龙提高+/省选−
CSP-S 2024 题解 A:决斗普及− B: 超速检测普及+/提高 C: 染色提高+/省选− D: 擂台游戏 NOI/NOI+/CTSC
CSP-J 2023 题解 A:小苹果普及− B: 公路普及− C: 一元二次方程普及/提高− D: 旅游巴士普及+/提高
CSP-S 2023 题解 A:密码锁普及− B: 消消乐提高+/省选− C: 结构体提高+/省选− D: 种树提高+/省选−
CSP-J 2022 题解 A:乘方入门 B: 解密普及− C: 逻辑表达式普及+/提高 D: 上升点列普及/提高−
CSP-S 2022 题解 A:假期计划提高+/省选− B: 策略游戏普及+/提高 C: 星战省选/NOI− D: 数据传输省选/NOI−
CSP-J 2021 题解 A:分糖果普及− B: 插入排序普及/提高− C: 网络连接普及/提高− D: 小熊的果篮普及+/提高
CSP-S 2021 题解 A:廊桥分配普及+/提高 B: 括号序列提高+/省选− C: 回文普及/提高− D: 交通规划省选/NOI−

一、廊桥分配

题意：一个机场有 n 个廊桥，需要分给国际机场航班和国内机场航班。
国际航班只能进入国际航班的廊桥，如果满了，就需要停到远机位。
国内航班只能进入国内机场的廊桥，如果停满了，一样也只能停到远机位。
每个航班都是优先停到廊桥，其次是远机位。
问如何分配，才能使得停留在廊桥的飞机尽量多。

思路：二分+线段树

如果可以预处理出每种廊桥数量对应的飞机数量，枚举所有分配方案，求和，取最大值即可。

假设廊桥数量无限，但有编号，航班会优先选择编号最小的廊桥。下面分析各航班如何匹配廊桥。
题意要求先到先得，所以先对航班到达时间 t 排序。

t0 时刻到达一个飞机后，我们需要找到所有空廊桥的最小编号。
空廊桥，意味着廊桥里面的飞机的离开时间小于 t0，即找到所有离开时间小于 t0 且编号最小的廊桥。

对于这个求小于一个值且最小编号的问题，可以使用二分线段树来做。

二分查找线段树前缀的最小值，直到找到第一个不满足条件的边界，下一个即为满足条件的位置。

sort(flights.begin(), flights.end());
segTree.Init(nm);
segTree.Build();
for (auto [a, b] : flights) {
  int l = 1, r = nm + 1;
  while (l < r) {
    int mid = (l + r) >> 1;
    if (segTree.QueryMin(1, mid) <= a) {
      r = mid;
    } else {
      l = mid + 1;
    }
  }
  nums[l]++;  // [a,b] 可以使用第 l 个廊桥
  ll oldVal = segTree.QueryMin(l, l);
  segTree.Update(l, b - oldVal);
}

每个航班最终选择哪个编号储存在 nums 中。
如果分配了 n 个廊桥，答案就是前 n 个 nums 的和，故预处理求前缀和。

for (int i = 1; i <= n; i++) {
  nums[i] += nums[i - 1];  // 前 i 个廊桥，最多可以容纳的飞机数量
}

最后枚举国际廊桥和国内廊桥的个数，求最大值。

int ans = 0;
for (int i = 0; i <= n; i++) {
  ans = max(ans, nums1[i] + nums2[n - i]);
}
printf("%d\n", ans);

二、括号序列

题意：给一个星号与括号匹配的规则，部分位置使用问号代替，问有多少种匹配方式。

规则1：() 和 (S) 为合法匹配，其中 S为至少1和不超过 k 个 * 。
规则2：如果 A 与 B 都是合法匹配，则 AB 和 ASB 也都为合法匹配。
规则3：如果 A 是合法匹配，则 (A) 、(AS)、(SA) 也都为合法匹配。

思路：语法解析动态规划

观察三个规则，可以确定一个结论：所有合法匹配，最左边肯定是左括号，最右边肯定是右括号。
这个结论是语法解析的基础，可以用来快速剪枝。

另外，这里的关键是对规则2进行划分，避免重复计算。
可以建最后状态1的状态转移方程解释。

状态定义：Dfs(l,r) 区间 [l,r] 内的合法匹配数量。
状态定义：DfsBracket(l,r) 命中规则3或规则1时，区间 [l,r] 内的合法匹配数量。状态定义：DfsLeft(l,r) 命中 SA 时，区间 [l,r] 内的合法匹配数量。
状态定义：DfsRight(l,r) 命中 AS 时，区间 [l,r] 内的合法匹配数量。

状态 DfsLeft 的转移方程：枚举星号的个数，至少1个，至多k个，然后递归求解。。

ll DfsLeft(const int l, const int r) {
  if (l > r) return 0;
  ll& ret = dpLeft[l][r];
  if (ret != -1) return ret;
  if (r - l + 1 < 3) return ret = 0;
  
  ret = 0;  // 至少1个，至多 k 个
  for (int i = 1; IsStart(l + i - 1) && i <= k && l + i <= r; i++) {
    ret = (ret + Dfs(l + i, r)) % mod;
  }
  return ret;
}

状态 DfsRight 的转移方程与状态 DfsLeft 类似。

ll DfsRight(const int l, const int r) {
  if (l > r) return 0;
  ll& ret = dpRight[l][r];
  if (ret != -1) return ret;
  if (r - l + 1 < 3) return ret = 0;

  ret = 0;  // 至少1个，至多 k 个
  for (int i = 1; IsStart(r - i + 1) && i <= k && l <= r - i; i++) {
    ret = (ret + Dfs(l, r - i)) % mod;
  }
  return ret;
}

状态 DfsBracket 的转移方程：根据题意分三种情况

ll DfsBracket(int l, int r) {
  if (l > r) return 0;
  ll& ret = dpBracket[l][r];
  if (ret != -1) return ret;
  if (l == r) return ret = 0;
  if (!MatchLeftBracket(l)) return ret = 0;
  if (!MatchRightBracket(r)) return ret = 0;
  ret = 0;
  // case: ()
  if (l + 1 == r) return ret = 1;

  // case: (*)
  if (IsAllStar(l + 1, r - 1) && r - l - 1 <= k) {
    ret = (ret + 1) % mod;
  }

  // case: (A)
  ret = (ret + Dfs(l + 1, r - 1)) % mod;

  // case: (*A)
  ret = (ret + DfsLeft(l + 1, r - 1)) % mod;

  // case: (A*)
  ret = (ret + DfsRight(l + 1, r - 1)) % mod;

  return ret;
}

状态 Dfs 用于处理多个合法匹配的拼接情况。

第一种是 ABSD，可以把 BSD当做一个合法匹配，按 AB规则来处理，即只需要枚举找到第一个 A即可。
第二种是 ASCD，可以把CD当做一个整体，按照 ASB 规则来处理。

ll Dfs(const int l, const int r) {  // [l,r]
  if (l > r) return 0;
  // 出口
  ll& ret = dp[l][r];
  if (ret != -1) return ret;
  if (l == r) return ret = 0;
  if (!MatchLeftBracket(l)) return ret = 0;
  if (!MatchRightBracket(r)) return ret = 0;
  if (l + 1 == r) return ret = 1;

  ret = 0;
  // case: (...)
  ret = (ret + DfsBracket(l, r)) % mod;

  // case: AB
  // bad case: ABCD, 只需要枚举到 A，故 A 必须是左右括号
  for (int i = l + 1; i + 1 < r; i++) {
    ret = (ret + DfsBracket(l, i) * Dfs(i + 1, r) % mod) % mod;
  }
  // case: A*B
  // bad case: AB*C, A*BC, AB*CD
  for (int i = l + 1; i + 1 <= r; i++) {
    ret = (ret + DfsBracket(l, i) * DfsLeft(i + 1, r) % mod) % mod;
  }

  return ret;
}

三、回文

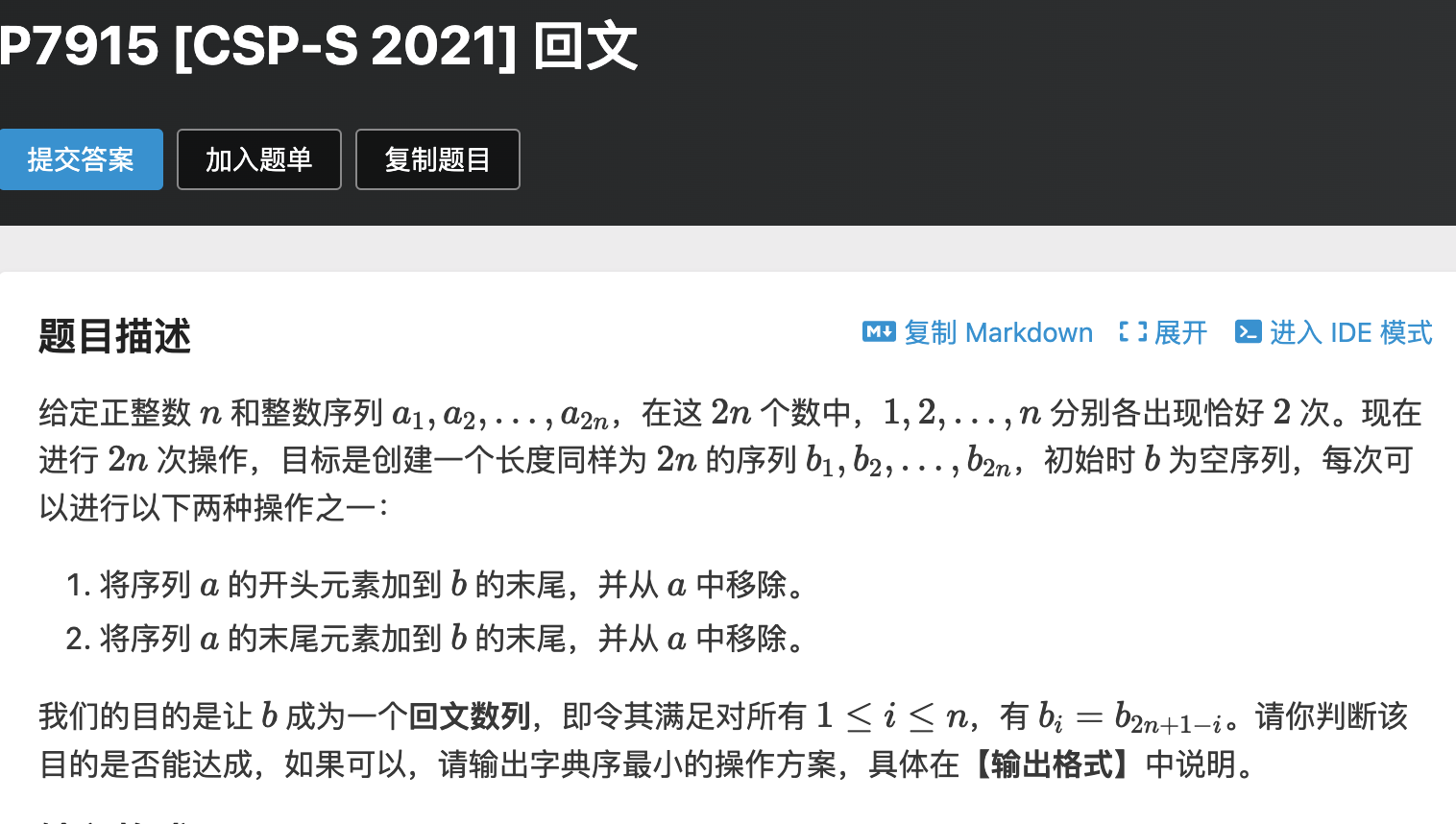
题意：给一个整数序列，每个数字恰好出现两次，问是否可以规则组成新的序列，使得新序列是回文序列。如果可以输出字典序最小的回文序列。
规则：每次从两端选择一个数字，将其加入新序列。

思路：构造+贪心搜索

假设第一个数字选择之后，就可以确定最后一个数字。
假设最后一个数字的位置在 x，则可以得到两个区间 [L,x-1] 和 [x+1, R]。

bool Check() {  //
  int p1 = 0, p4 = n2 + 1, p2, p3;
  // 尝试左端点
  ans.push_back('L');
  p1++;
  p2 = p3 = indexs[nums[p1]].back();  // 选择左边的，另一个值在右边
  if (Check(p1, p2, p3, p4, 1)) {
    ans.push_back('L');
    return true;
  }
  ans.pop_back();
  p1--;

  // 尝试右端点
  ans.push_back('R');
  p4--;
  p2 = p3 = indexs[nums[p4]].front();  // 选择右边的，另一个值在左边
  if (Check(p1, p2, p3, p4, 1)) {
    ans.push_back('L');
    return true;
  }
  return false;
}

第二个数字可以选择 L 或 R，无论选择哪一个，若想有解，则第二个数字回文对称的位置必须在 x-1 或者 x+1。
基于这个逻辑，就可以递归搜索了。

bool Check(int p1, int p2, int p3, int p4, int num) {  // (p1,p2), (p3,p4)
  if (num == n) {                                      // 找到一组答案
    return true;
  }
  // 尝试选择左端点
  if (p1 + 1 < p2) {
    ans.push_back('L');
    p1++;
    if (p2 - 1 > p1 && nums[p1] == nums[p2 - 1] && Check(p1, p2 - 1, p3, p4, num + 1)) {
      ans.push_back('L');
      return true;
    }
    if (p3 + 1 < p4 && nums[p1] == nums[p3 + 1] && Check(p1, p2, p3 + 1, p4, num + 1)) {
      ans.push_back('R');
      return true;
    }
    ans.pop_back();
    p1--;
  }
  // 尝试选择右端点
  if (p3 + 1 < p4) {
    ans.push_back('R');
    p4--;
    if (p2 - 1 > p1 && nums[p2 - 1] == nums[p4] && Check(p1, p2 - 1, p3, p4, num + 1)) {
      ans.push_back('L');
      return true;
    }
    if (p3 + 1 < p4 && nums[p3 + 1] == nums[p4] && Check(p1, p2, p3 + 1, p4, num + 1)) {
      ans.push_back('R');
      return true;
    }
    ans.pop_back();
    p4++;
  }
  return false;
}

可以构造一组数据，使得每次都可以选择左边或右边，因此复杂度为 O(2^n)。
case: 1 2 5 6 7 4 3 1 2 5 7 6 4 3
得分：64。

优化：记忆化搜索，得分 92。

set<tuple<int, int, int, int>> H;
bool Check(int p1, int p2, int p3, int p4, int num) {  // (p1,p2), (p3,p4)
  const tuple<int, int, int, int> tup = make_tuple(p1, p2, p3, p4);
  if (H.count(tup)) {
    return false;
  }
  H.insert(tup);
  // 搜索
}

优化：超时的原因在于有时既可以选择左边也可以选择右边。
可以证明，这两种选择是等价的，即要么都有解，要么都无解。
因此，只需选择字典序更小的左边即可。
复杂度：O(n)

bool Check(const int p1, const int p2, const int p3, const int p4, int num) {  // (p1,p2), (p3,p4)
  if (num == n) {  // 找到一组答案
    return true;
  }
  // 尝试选择左端点
  if (p1 + 1 < p2 && p2 - 1 > p1 + 1 && nums[p1 + 1] == nums[p2 - 1]) {
    ans.push_back('L');
    if (Check(p1 + 1, p2 - 1, p3, p4, num + 1)) {
      ans.push_back('L');
      return true;
    } else {
      ans.pop_back();
      return false; // 剪枝，直接返回没答案
    }
  }
  // 下面的代码都一样，加上剪枝代码
  return false;
}

四、交通规划

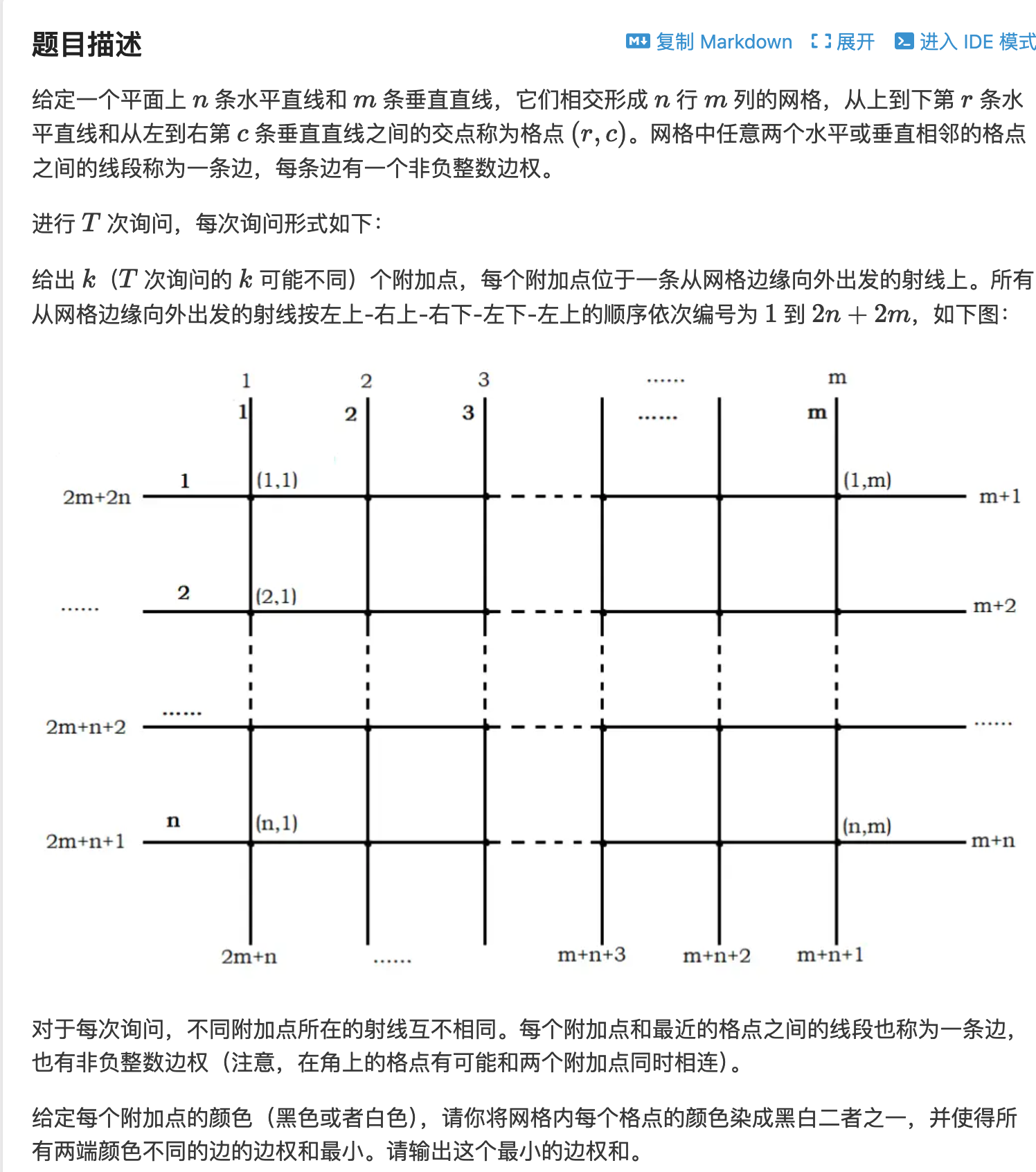
题意：n个横线，m个竖线形成一个网格，输入会告诉所有横线线段的权重与竖线线段的权重。
如上图，横线与竖线周围还有2*(n+m)条射线，按顺时针编号。
现在会在 k 个射线上分别新增一个点，从而增加 k 个带权重的线段。
另外，这 k 个点有黑白两种颜色，问如何对网格的点进行颜色，才能使得左右端点颜色不同的线段的权重和。

思路：对偶图+最短路+环形DP

想到了对偶图，但是依旧没思路。
最后看了题解，原来有几个性质，根据这个性质，可以发现2个点其实就是求最短路。
多个点时，由于哪个最短路是最优的无法确定，所以需要使用环形DP来求解。

假设只有两个颜色不同的点，则很容易想到，需要找到一条路径，将原始图划分为两部分，使得上部分全为一种颜色，下部分全为另一种颜色，且该路径经过的边权和最小。

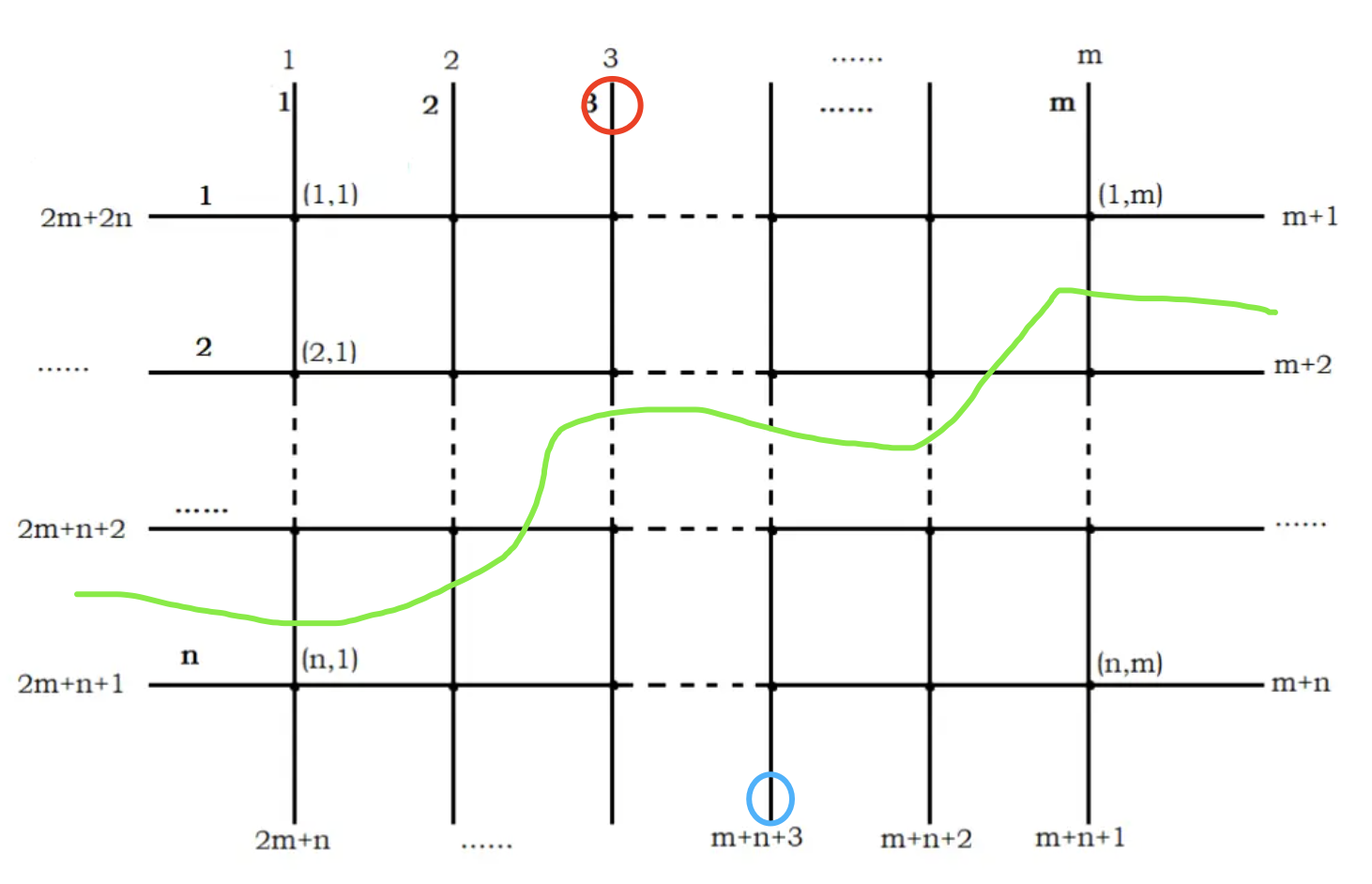
对偶图，就是将原图的面转化为点的图。
转化为对偶图后，两边分别加上超源点和超汇点，这样的一个路线恰好就是图的最短路。

故，对于只有2个点的情况，可以直接构图与求最短路即可。
得分:45。

如果点大于两个后，该怎么处理呢？

假设网格是无限的，外面也需要涂色，但是边的权重是0。
我们可以分析涂色的区域，可以得到下面几个结论。

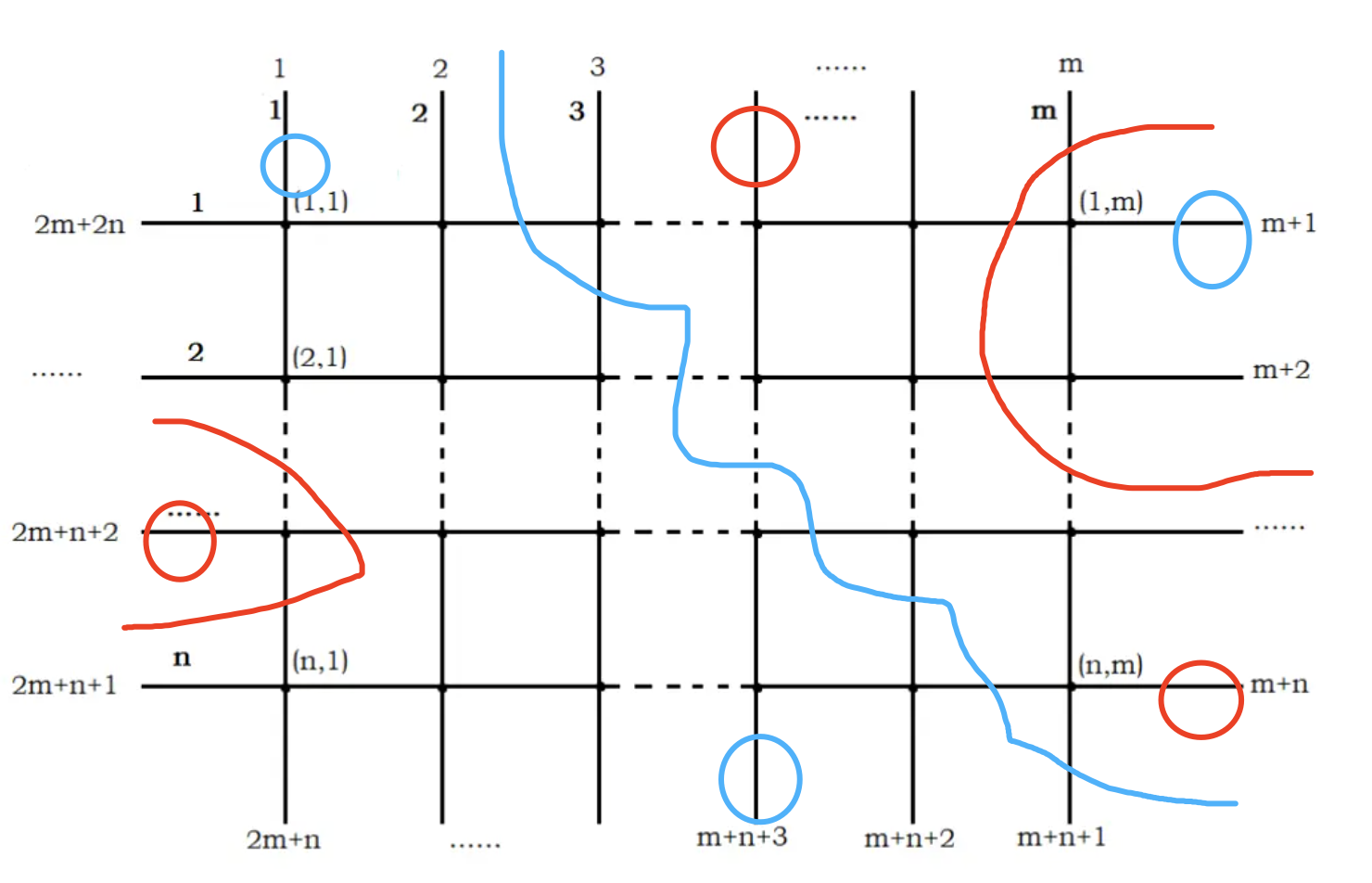
结论1：相邻两个相同颜色的点，可以按1个点处理，合并缩点后剩余黑白相邻共偶数个点，。
结论2：涂色之后，颜色的分割线组成线路就是一条最短路。
结论3：分割线同侧颜色需要保持一致。
结论4：分割线之间，不存在交叉情况。
结论5：合并缩点后，任何相邻点之间，必然有一个分割线（颜色不同）。

根据这个结论，可以发现，这个和多边形的三角形拆分是类似的。

对偶图构图：
顶点颜色：定义每个顶点的颜色与顺时针的平面保持一致。

求k个顶点之间的最短路：求k次单源最短路。

indexDis.clear();
indexDis.resize(k, vector<ll>(k, INFL));
for (int i = 0; i < k; i++) {
  SolverMinPath(i);
}

min_queue<pair<ll, int>> q;
int K;
void SolverMinPath(const int kIndex) {
  const int gp1 = get<1>(points[kIndex]);
  // 计算 gp1 到其他点的最短路径
  fill(vis.begin(), vis.end(), INFL);
  while (!q.empty()) {
    q.pop();  // 清空队列
  }
  auto Add = [&](int gP, ll cost) {
    if (vis[gP] <= cost) return;
    vis[gP] = cost;
    q.push({cost, gP});
  };
  Add(gp1, 0);
  int findKpNum = 0;
  while (!q.empty()) {
    const auto [SCost, SgP] = q.top();
    q.pop();
    if (vis[SgP] < SCost) continue;
    // MyPrintf("gp1=%d SgP=%d, SCost=%lld\n", gp1, SgP, SCost);
    if (gPointTokPoint.count(SgP)) {  // 找到一个 kp 最短路
      const int SkP = gPointTokPoint[SgP];
      const int SkIndex = kPointToKIndex[SkP];
      indexDis[kIndex][SkIndex] = min(indexDis[kIndex][SkIndex], SCost);
      findKpNum++;
      if (findKpNum == K) break;  // 剪枝，找到所有 kp
    }
    for (const auto& [TgP, TCost] : g[SgP]) {
      Add(TgP, SCost + TCost);
    }
  }
}

求出了所有顶点之间的最短路后，就是枚举所有划分，求最优解。

// 第二步：计算环形DP的最优值
dp.clear();
dp.resize(k, vector<ll>(k, -1));
ll ans = INFL;
for (int a = 0; a < k; a++) {
  for (int b = a + 1; b < k; b += 2) {  // 奇数点只能连偶数点
    ans = min(ans, indexDis[a][b] + Dfs(a, b) + Dfs(b, a));
  }
}

状态定义：Dfs(a,b) a已经与b相连的情况下，a 顺时针到 b 的顶点进行划分的最优解。

由于对偶图的顶点颜色是顺时针继承原始图的顶点颜色，所以 a 顶点不在求解范围之内，故区间是左开右闭(a, b]。

根据结论5：合并缩点后，任何相邻点之间，必然有一个分割线（颜色不同）。
这里可以枚举 a+1 为起始位置的分割线，共有 b-a-1中情况，枚举所有情况，求最小值。

vector<vector<ll>> dp;
ll Dfs(const int A, const int B) {  // (a,b]
  int a = A, b = B;
  ll& ret = dp[a][b];
  if (ret != -1) return ret;

  ret = INFL;
  if (a > b) {
    b += K;  // 环形，保证 a < b
  }
  if (a == b || a + 1 == b) return ret = 0;  // 相同颜色，不需要继续拆分
  a++;                                       // a 已经被分割在外面
  for (int i = a + 1; i <= b; i += 2) {      // 枚举分割点
    ret = min(ret, indexDis[a % K][i % K] + Dfs(a % K, i % K) + Dfs(i % K, b % K));
  }
  MyAssert(ret != INFL);
  return ret;
}

到这里，可以得 80分，剩余 4 组数据超时。

分析复杂度如下：

输入复杂度：O(n*m)
询问 T 组，每组 K 个点。
K 个点排序去重，O(K log(K))
K 个点构图，O(n*m)
求K次最短路，O(K * E)，稀疏图，大概为O(K * (n+m)) 环形DP，复杂度 O(K^3)

综合复杂度：O(T * (n*m + K*(n+m) + K^3))

可以发现，最耗时的地方在于构图，每次需要 O(n*m)。

而对偶图每次只有最外围的顶点会变化，其余部分保持不变。
因此，构图可以拆分为两部分：一部分是始终不变的内层，另一部分是每次单独在内层基础上追加的外层。
构图的复杂度每次就可以降低到 O(n+m)，从而得到 100 分。

五、最后

这次比赛其实挺难的。
第一题两个维度的最值，本想使用树套树，最终发现可以二分。
第二题最简单，语法解析动态规划。
第三题需要推导出同时有答案，从而直接贪心搜索即可。
第四题则非常难，对偶图里求最短路，然后环形DP，代码量相当大。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。