leetcode 第 462 场算法比赛
作者: | 更新日期:
数位DP
本文首发于公众号:天空的代码世界,微信号:tiankonguse
零、背景
这次比赛最后一题是数位DP,我想直接贪心做,结果越写越复杂,最后在比赛前没通过比赛。
赛后老老实实写数位DP,就通过了。
A: 模拟
B: 贪心
C: 贪心
D: 数位DP
排名:158
代码地址: https://github.com/tiankonguse/leetcode-solutions
一、垂直翻转子矩阵

题意:给一个矩阵,对指定的子矩阵进行上下翻转。
思路:模拟
for (int j = y; j < y + k; j++) {
for (int i0 = x, i1 = x + k - 1; i0 < i1; i0++, i1--) {
swap(grid[i0][j], grid[i1][j]);
}
}
二、排序排列

题意:给一个数组,求选择一个k,可以对任意两个与运算等于k的位置进行交换。
求最大的k,使得通过交换最终可以使得数组有序。
思路:贪心
分析可以得到下面几个结论:
结论1:下标和值不相等的值,都是需要交换的。
结论2:一个待交换的元素某一位是 0,则 k 这一位也是 0。
即所有待交换的元素,只要有一个某一位是0,则 K 这以为都是 0。
结论3:如果所有待交换的元素某一位都是 1,则 k 这一位可以是 1。
综合上面的结论,可以推导出所有需要交换的元素一起进行与运算,就是最小的 k。
使用这一个最小 K,循环交换,就可以将数组变成有序。
具体交换规则是:
规则1:消除K所在的循环节。
假设值 K 所在的下标是 P,则使用值 K 与值交换,这样一直交换下去,就可以把一个循环节的值都交换到排序后的位置。
规则2:K 加入新的循环节。
如果还存在其他错位的循环节,随便选择循环节的位置与 K 交换,这样 K 就加入到循环节了,之后再次按上述规则交换,则可以再次消除这个循环节。
规则3:消除所有循环节
int ans = ~0;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] != i) {
ans = ans & i;
}
}
if (ans == ~0) ans = 0;
return ans;
三、最优激活顺序得到的最大总和

题意:有n个元素,每个元素有一个最低限制和收益值,然后按规则进行选择元素。
规则1:默认所有元素都是非活跃的。
规则2:当前活跃数严格小于一个元素的最低限制时,才可以选择这个元素,当前元素激活,并获取收益。
规则3:激活一个元素后,所有最低限制值小于等于当前活跃数的元素,都会变为非活跃,并且永远无法选择。
求最大收益值。
思路:贪心。
分析规则2,显然,对于相同的限制值,肯定优先选择收益值最大的元素。
而对于不同限制值的元素,则需要从小到大来选择。
分析规则3,假设当前活跃数是 n-1,选择了最低限制n的最大收益元素,活跃数会变成n,然后最低限制为n的其他元素都会标记为无法选择。
另外最低限制小于 n的都需要转化为非活跃状态,这意味什么呢?
假设每个限制值都有无数个元素,可以发现一个规律。
limit=1: 最多选择1个值,此后活跃数清空
limit=2: 最多选择2个值,此后活跃数清空
...
limit=n: 最多选择n个值,此后活跃数清空
如果限制值中间有空档或者不是无限的,也不影响上面的规律。
故,可以先按限制值排序,相同的按收益逆序排序,之后维护两个数据结构来模拟。
第一个是最大活跃数状态 S,代表最低限制小于等于 S 的元素,都已经标记为无法选择。
第二个是选择的活跃元素队列,用于出队并标记为永久无法选择。
ll ans = 0;
int x = 0;
int maxX = 0;
queue<ll> que;
for (auto [la, va] : nums) {
if (x < la && maxX < la) {
ans += va;
que.push(la);
x++;
maxX = max(maxX, x);
while (!que.empty() && que.front() <= x) {
que.pop();
}
x = que.size();
}
}
return ans;
当然,也可以基于限制值对数组分组,每个分组求 TOP limit 的元素和即可。
下面的代码为了性能,直接在一维数组上通过游标来区分分组的边界。
ll ans = 0;
ll nowLimit = 0;
ll nowNum = 0;
for (auto [la, va] : nums) {
if (nowLimit != la) {
nowLimit = la;
nowNum = 0;
}
if (nowNum < la) {
ans += va;
nowNum++;
}
}
return ans;
四、下一个特殊回文数

题意:给一个整数 n,求一个大于 n 的最小的整数,要求这个数字是回文数,且数字中每个数字 k 出现 恰好 k 次。
思路:数位DP。
数据范围是 10^15,考虑回文对称性,其真实数据范围只有 10^8。
再分析每个数字 k 出现 恰好 k 次,可以得到下面几个结论。
结论1:数字长度为奇数时,奇数数字只能出现一次,且中间的数字就是奇数。
结论2:数字长度为偶数时,出现的数字必须全部是偶数。
例如各个长度的答案如下:
len=1: 1
len=2: 22
len=3: 212,333
len=4: 4444
len=5: 44144 55555, 23332, 32323
len=6: 244442 424424 442244
...
观察规律,发现每个长度的回文数很少,且个数等于长度的数字拆分的排列数。
1到15的数字拆分如下:
1=1
2=2
3=31+2, 3
4=4
5=1+4, 3+2, 5
6=2+4, 6
7=1+6, 1+2+4, 3+4
8=2+6, 8
9=1+8, 1+2+6, 3+6, 3+2+4, 5+4
10=2+8, 4+6
11=1+10, 1+2+8, 1+4+6, 3+8, 3+2+6, 5+6, 5+2+4, 7+4, 9+2, 11
...
可以发现,不管怎么选择,只能选择1个奇数,4个偶数,最多选择 5 个数字。
之后是这5个数字的排列组合,复杂度并不高。
针对这个规律,有两个方法。
方法1:先数字拆分,然后排列组合枚举求出所有符合条件的回文数,然后计算出答案。
方法2:数位DP,从小到大枚举,找到第一个满足要求的即结束。
对于奇数,比较特殊,所以需要枚举所有情况,求最小值。
// 求大于 n 的长度为 len 的答案,其中 n 的长度也是 Len
ll TryLen(int len) {
if (len % 2 == 0) {
fill(bits, bits + 10, 0);
if (DfsAll(len, 0, 0, 0)) {
return dfsAns;
}
} else {
ll ans = INFL; // 奇数1+8 可能不是最优答案,例如 5+4 会更小
for (int mid = 1; mid < 10; mid += 2) {
fill(bits, bits + 10, 0);
bits[mid]++;
dfsAns = INFL;
if (DfsAll(len, mid, 0, mid * B[len / 2])) {
ans = min(ans, dfsAns);
}
}
if (ans != INFL) {
return ans;
}
}
return 0;
}
优化:每一个长度都存在答案,如果n所在的长度没有答案,直接选择 n+1长度的最小值即可。
ll ans = TryLen(len);
if (ans > 0) {
return ans;
}
return TryLen(len + 1);
数位DP 可以直接从高位到低位枚举每一位的数值,最终判断是否满足个数要求即可。
bool DfsAll(const int len, const int mid, const int offset, const ll val) {
if (offset == len / 2) {
// 先检查 数字中每个数字 k 出现 恰好 k 次
if (mid > 0 && bits[mid] != mid) {
return false;
}
for (int i = 2; i < 10; i += 2) {
if (bits[i] > 0 && bits[i] != i) {
return false;
}
}
if (this->n < val) {
dfsAns = val;
return true;
} else {
return false;
}
}
for (int i = 2; i < 10; i++) { // 从小到大枚举,确保答案是最小的
if (bits[i] < i && (i == mid || i % 2 == 0)) {
bits[i] += 2;
if (DfsAll(len, mid, offset + 1, val + i * B[offset] + i * B[len - 1 - offset])) {
return true;
}
bits[i] -= 2;
}
}
return false;
}
优化1:可以一边枚举一边检查个数是否满足要求。
// leftLen 一次也没选择的数字里面,允许选择的数字个数
// bool DfsAll(const int len, const int mid, const int offset, const ll val, const int leftLen)
for (int i = 2; i < 10; i++) { // 从小到大枚举,确保答案是最小的
if (bits[i] == i) continue; // 足够了
if (bits[i] == 0 && i > leftLen) continue; // 剪枝,首次选择,剩余位置不够
if (i == mid || i % 2 == 0) {
int newleftLen = leftLen;
if (bits[i] == 0) {
newleftLen -= i; // 首次选择,一次性全部扣除
}
bits[i] += 2;
const ll newVal = val + i * B[offset] + i * B[len - 1 - offset];
if (DfsAll(len, mid, offset + 1, newVal, newleftLen)) {
return true;
}
bits[i] -= 2;
}
}
优化2:从小到大枚举时,可能当前枚举前缀已经小于 n 的前缀,此时可以直接跳过。 由于只有长度相同时才需要比较前缀,这里可以记录当前枚举的最大值,从而做到通用性。
// leftLen 一次也没选择的数字里面,允许选择的最大数字
// leftMaxVal 未填充位置全部是 9 的值
bool DfsAll(const int len, const int mid, const int offset, const ll val, const int leftLen, const ll leftMaxVal) {
if (val + leftMaxVal < this->n) return false;
if (offset == len / 2) {
// 出口
}
for (int i = 2; i < 10; i++) { // 从小到大枚举,确保答案是最小的
if (bits[i] == i) continue; // 足够了
if (bits[i] == 0 && i > leftLen) continue; // 剪枝,首次选择,剩余位置不够
if (i == mid || i % 2 == 0) {
int newleftLen = leftLen;
if (bits[i] == 0) {
newleftLen -= i; // 首次选择
}
bits[i] += 2;
const ll newVal = val + i * B[offset] + i * B[len - 1 - offset];
const ll newLeftMaxVal = leftMaxVal - 9 * B[offset] - 9 * B[len - 1 - offset];
if (DfsAll(len, mid, offset + 1, newVal, newleftLen, newLeftMaxVal)) {
return true;
}
bits[i] -= 2;
}
}
return false;
}
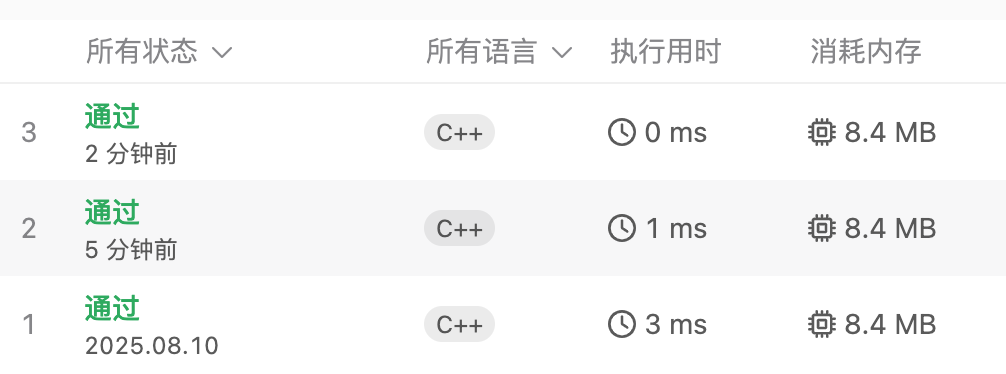
三次代码的耗时对比,没有任何优化是3ms,加上长度优化是1ms,加上前缀优化是0ms。
五、最后
这次比赛最后一题有点难度,第二题和第三题的贪心也不好证明,整体比赛难度上来了。
第四题比赛的时候我想到了数位DP,但是发现也可以直接进行数字拆分与排列组合,于是就写了数字拆分和排列组合的代码,结果发现代码量很大,时间就不够了。
《完》
-EOF-
本文公众号:天空的代码世界
个人微信号: tiankonguse
公众号 ID: tiankonguse-code
本文首发于公众号:天空的代码世界,微信号:tiankonguse
如果你想留言,可以在微信里面关注公众号进行留言。
