leetcode 第 466 场算法比赛

零、背景

这次比赛第三题二分单调栈，第四题数位DP，没想到过得人这么多。

A: 简单计算
B: 简单计算
C: 二分单调栈
D: 数位DP

排名：200
代码地址： https://github.com/tiankonguse/leetcode-solutions

一、数组元素相等的最小操作次数

题意：每次可以修改一个子数组的值，问修改多少次可以让数组所有元素相等。

思路：简单计算

显然，需要修改时，直接修改整个数组即可。
故需要修改则答案为1，否则答案为0。

二、转换字符串的最小操作次数

题意：给一个小写字母的字符串，每次可以选择值相同的字符全部修改为循环字典序下个字符。
问最少修改几次，所有字符修改为 a。

思路：简单计算

由于每次可以修改值相同的字符，所以与字符个数与顺序无关，至于不同值有关。

如果存在两个不同值，显然需要修改小的，等到与大的值一样了，再一次修改。
故答案由非a得最小值决定。

求出这个最小值，再求需要修改的次数即可。

vector<int> count(26, 0);
for (char c : s) {
  count[c - 'a']++;
}
for (int i = 1; i < 26; i++) {
  if (count[i] > 0) {
    return 26 - i;
  }
}
return 0;

三、碗子数组的数目

题意：给一个数组，问有多少个连续子数组，使得子数组中间的值都不大于左右端点的值。

思路：二分单调栈

暴力做法是枚举所有子数组，然后使用线段树求区间最大值，判断是否满足要求，复杂度O(n^2 log(n))。

子数组问题，显然需要枚举一个端点，然后在一个数据结构里，判断另一个端点集合里有多少满足要求的个数。

这里枚举右端点，维护左端点的集合。
由于中间的值都需要小于左右端点的值，所以可以使用单调栈，维护一个单调递减的栈。
具体来说，最后一个元素需要入栈，如果之前的元素小于最后一个元素，则都需要出栈。

然后分析这个栈，发现栈分两部分：

如下图，R 部分的值都小于当前右端点，故满足中间的值都小于左右端点的值，但需要排除最后一个元素。
而 L 部分的值，左端点大于右端点，只有最后一个满足要求，再往前的，就存在中间的值大于右端点了。

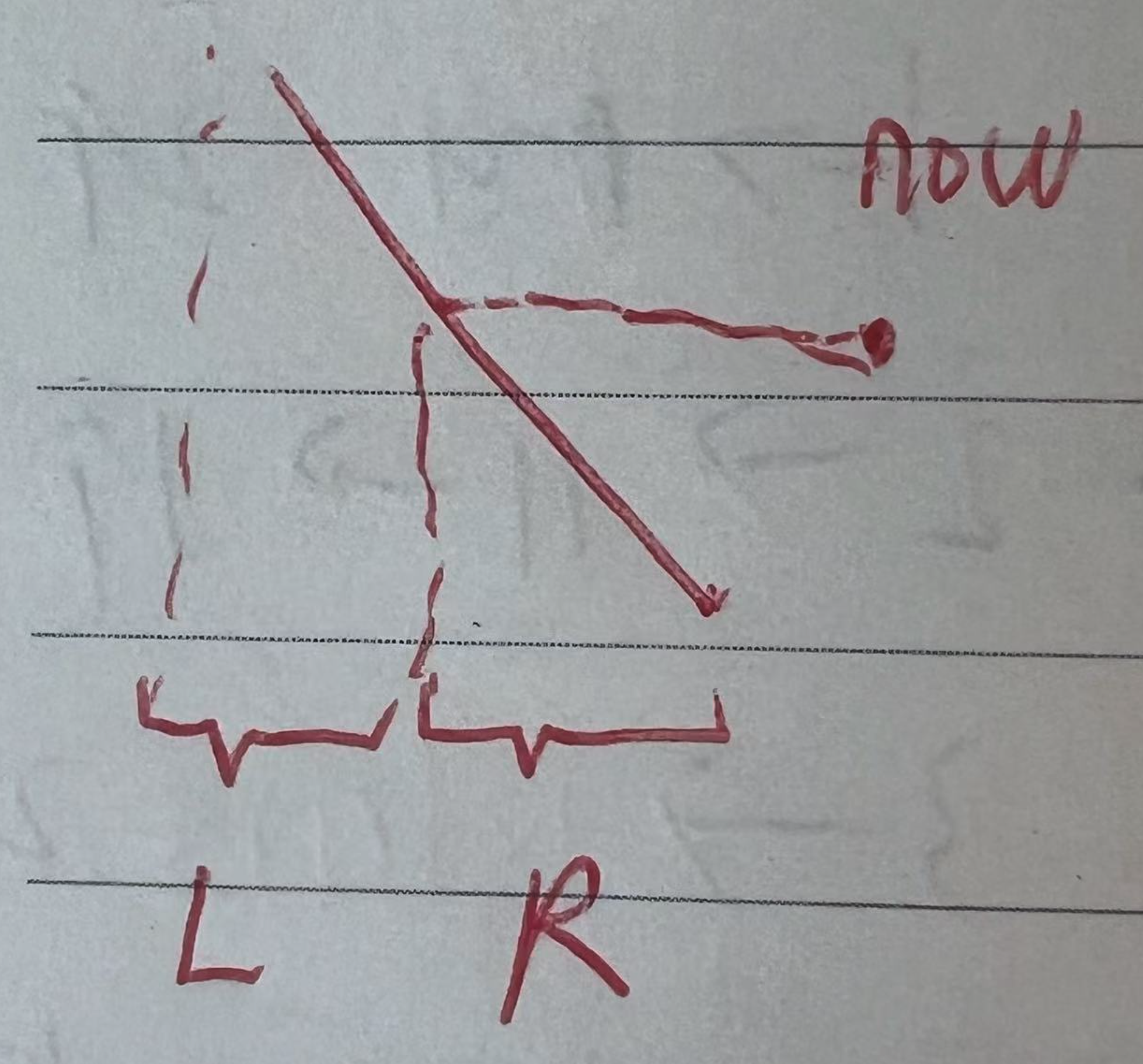
PS: 为了避免自己写二分查找，这里我使用负数储存，从而可以使用 lower_bound二分查找。

ll ans = 0;
for (int i = 0; i < n; i++) {
  const int v = nums[i];
  if (sta.size() > 1 && Abs(sta.back()) < v) {  // 长度至少为 3
    auto it = std::lower_bound(sta.begin(), sta.end(), -v);
    ans += sta.end() - it - 1;
    if (it != sta.begin()) {
      ans++;  // 只能选择一个大于 右端点的值
    }
  }
  while (!sta.empty() && Abs(sta.back()) < v) {
    sta.pop_back();
  }
  sta.push_back(-v);
}
return ans;

比赛的时候，我是假设右端点大于左端点，然后分别求出 R 部分的。

ll ans1 = bowlSubarraysEx(nums);
std::reverse(nums.begin(), nums.end());
ll ans2 = bowlSubarraysEx(nums);
return ans1 + ans2;

进一步分析单调栈，假设右半部有 R 个元素，则接下来维护单调栈时，需要出栈 R 个元素。
出栈后，如果堆栈还有元素，则显然这个元素就可以当做左端点答案。
故可以边出栈边计算答案。

ll ans = 0;
for (int i = 0; i < n; i++) {
  const int v = nums[i];
  while (!sta.empty() && Abs(sta.back()) < v) {
    sta.pop_back();
    if (!sta.empty()) {
      ans++; // [sta.back(), v] 区间可以组成一个答案
    }
  }
  sta.push_back(-v);
}
return ans;

神奇，答案个数竟然不大于 N。

四、统计二进制回文数字的数目

题意：给一个数字 n，求二进制表示下，有多少不大于n的二进制数字是回文数。

思路：经典的数位DP。

假设 n 的二进制数位为 B，根据状态可以划分为三部分：

1）数字二进制位数小于 B，则可以是任意回文二进制数字，答案固定，可以直接计算出来。
2）对于n位的二进制，从高位开始，如果 n 对应位值是 1, 则可以取值 0，接下来的剩余位数可以是带前缀0的任意回文二进制数字，答案固定，可以直接计算出来。
3）如果取值等于 n 对应的位值，则递归到下一位判断。
3）如果位数越过中界限，需要判断高位镜像过来后，是否不大于 n，不大于了也算一个答案。

允许前缀 0 的 B 位回文个数为 2^{(B+1)/2}。
不允许前缀 0 的 B 位回文个数为 2^{(B-1)/2}。

ans = 1;  // 0 答案是1
for (int i = 1; i < B; i++) {
  ans += one << ((i - 1) / 2);  // 各位任意值的答案，边界必须为1
}

数位DP 则是从高位开始，枚举取值，依次计算答案，复杂度 log(n)。

void Dfs(int k) {
  if (k < B2) {
    // 需要检查低位一半是否大于高位一半，大于了也有一个答案
    for (int i = B2 - 1; i >= 0; i--) {
      if (bits[i] > bits[B - 1 - i]) {
        ans++; // 大于，有答案
        return;  
      } else if (bits[i] < bits[B - 1 - i]) {
        return;  // 小于没答案
      }
    }
    ans++;  // 相等也有一个答案
  } else {
    if (bits[k] == 1) {          // 取 0 时，后面的都是答案
      ans += (one << (k - B2));  // 各位任意值的答案，边界可以是0
    }
    Dfs(k - 1);  // 取值与 bits[k] 相同
  }
}

五、总结

这次比赛前两道题非常简单。
第三题单调栈竟然可以一步步推导出答案很小的结论。
第四题是一个经典的数位DP。
总的看下来，第三题应该比第四题难得，毕竟单调栈需要深度思考，而数位DP只是一个模版题。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号： tiankonguse
公众号 ID： tiankonguse-code