leetcode 第 467 场算法比赛-56名

零、背景

这次比赛比较简单，我昨晚没睡好，也进入到了第56名

A: 循环最小值
B: 排序去重
C: 背包DP
D: 状态DP

排名：56
代码地址： https://github.com/tiankonguse/leetcode-solutions

一、完成一个任务的最早时间©leetcode

题意：给你一个二维整数数组 tasks，其中 tasks[i] = [si, ti]。
数组中的每个 [si, ti] 表示一个任务，该任务的开始时间为 si，完成该任务需要 ti 个时间单位。
返回至少完成一个任务的最早时间。

思路：循环，求最小值

std::accumulate(
  tasks.begin(), 
  tasks.end(), 
  INT_MAX,
  [&](int a, const auto& b) { 
    return min(a, b[0] + b[1]); 
  }
);

二、至多 K 个不同元素的最大和

题意：给你一个正整数数组 nums 和一个整数 k。
从 nums 中选择最多 k 个元素，使它们的和最大化。但是，所选的数字必须互不相同。
返回一个包含所选数字的数组，数组中的元素按严格递减顺序排序。

思路：排序去重 TOP K

sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
reverse(nums.begin(), nums.end());
if (nums.size() > k) {
  nums.resize(k);
}
return nums;

三、含上限元素的子序列和

题意：依次处理数组，如果元素的值大于 x 则修改为 x。问是否存在一个子序列，使得子序列的和为 k。

思路：背包DP

元素个数和值域都是 10^3，问元素和恰好匹配，典型的背包问题。

由于是子序列，所以元素位置无关，可以先排序。

元素值大于 x 时修改为 x，显然，x 之前的都不变，之后的都需要修改。
故可以从小到大枚举x，对小于等于 x 的进行背包DP，大于 x 的值存在修改，不能加入背包，直接暴力枚举即可。

vector<int> dp(k + 1, 0);
dp[0] = 1;
sort(nums.begin(), nums.end());
int p = 0;
for (int x = 1; x <= n; x++) {
  while (p < n && nums[p] <= x) {
    Add(nums[p]);
    p++;
  }
  ans[x - 1] = Check(n - p, x);
}

背包DP：dp(i) 之前的元素是否存在和为 i 的子序列。
状态转移方程： dp(i+v) = dp(i+v) || dp(i)

背包DP有一个空间优化，由于计算后面的状态时依赖前面的状态，故需要从大到小枚举状态，这样才能保证前面的状态不会被覆盖。

auto Add = [&](int v) {
  if (dp[k] == 1) {
    return; // 剪枝
  }
  for (int i = k; i >= 0; i--) {
    if (dp[i] == 1 && i + v <= k) {
      dp[i + v] = 1;
    }
  }
};

对于大于 x 的元素，直接暴力枚举即可。

auto Check = [&](int leftNum, int x) {
  for (int i = 0; i <= leftNum; i++) {
    if (i * x > k) return false; // 剪枝
    if (dp[k - i * x] == 1) return true;
  }
  return false;
};

复杂度：O(n^2)

四、稳定子序列的数量

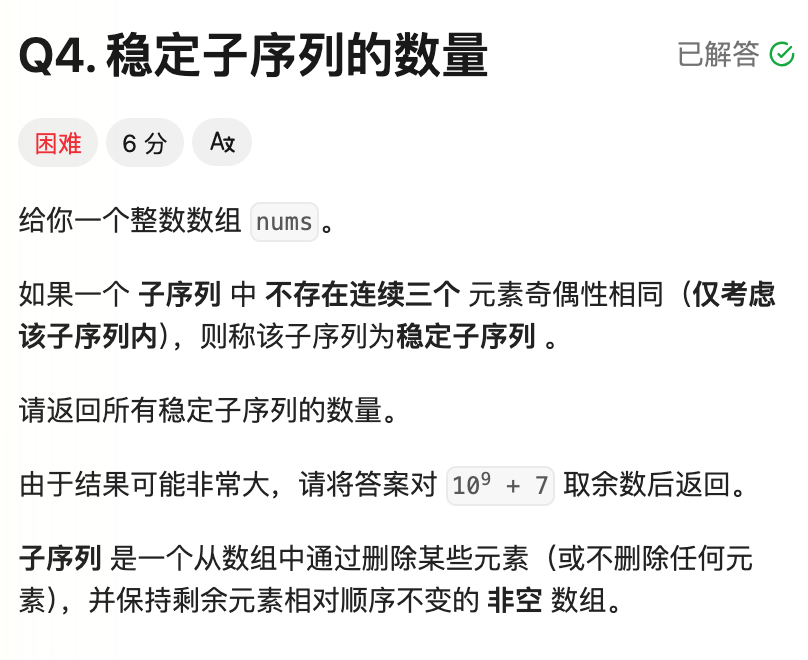
题意：给一个数组，问存在多少个子序列，子序列中不存在连续3个相同奇偶性的元素。

思路：状态DP

状态定义: dp(s) 之前的所有元素组成的有效子序列中，状态为 s 的子序列数量。

可能得合法状态：

$ // 空
$0 // 只有一个元素，且为偶数
$1 // 只有一个元素，且为奇数
00 // 至少两个元素，且最后两个元素为偶数
01 // 至少两个元素，为偶数+奇数
10 // 至少两个元素，为奇数+偶数
11 // 至少两个元素，且最后两个元素为奇数

可能得非法状态

000
111

再来一个数字后，我们可以根据当前状态和新数字的奇偶性，来更新状态。

状态转移方程：

dp[n](s) = dp[n-1](s) + sum(dp[n-1](NextState(s0, v)))

解释：当前位置某个状态的答案分为两部分，一部分是之前的答案，一部分是当前元素的答案。
当前元素的答案，需要枚举之前的所有状态，然后根据当前元素的奇偶性，得到新的状态，进行累加。

由于状态之间存在互相跳转，所以可以使用滚动数组进行空间优化。
当然，由于只需要前面一个位置的状态，这里我直接使用临时数组来代替。

vector<ll> dp(E_END, 0);
dp[E_EMPTY] = 1;

vector<ll> next(E_END, 0);
for (auto v : nums) {
  fill(next.begin(), next.end(), 0);
  for (int i = 0; i <= E_11; i++) {
    int s = NextState(i, v % 2);
    next[s] = (next[s] + dp[i]) % mod;
  }
  for (int i = 0; i <= E_11; i++) {
    dp[i] = (dp[i] + next[i]) % mod;
  }
}
ll ans = 0;
for (int i = E_0; i <= E_11; i++) {
  ans = (ans + dp[i]) % mod;
}
return ans;

计算新状态时，可以发现状态分为三部分：空、1位、2位。

空状态只能转化为1位状态。
1位状态只能转化为2位状态。
2位状态只能转化为2位状态。

另外，还可以发现，状态是二进制的关系，故直接可以使用位运算进行计算。
由于存在非法状态，实现的时候，我们使用特殊状态 E_OTHER 标识。

enum { E_EMPTY, E_0, E_1, E_00, E_01, E_10, E_11, E_OTHER, E_END };
int NextState(int s, int v) {
  if (s == E_EMPTY) {
    return E_0 + v;
  } else if (s == E_0 || s == E_1) {
    return E_00 + (s - E_0) * 2 + v;
  } else {
    int tmp = (s - E_00) * 2 + v;
    if (tmp == 0 || tmp == 7) {
      return E_OTHER; // 非法状态
    } else {
      return E_00 + (tmp % 4);
    }
  }
}

PS：赛后看了榜单，状态定义为 dp[v][len]代码会更简单。
状态含义：以 len 个 v 结尾的子序列个数。

状态转移方程：

dp[v][2] = (dp[v][2] + dp[v][1]) % mod
dp[v][1] = (dp[v][1] + dp[v^1][1] + dp[v^1][2] + 1) % mod

解释：长度为2的只能是长度为1的转换过来。
长度为1的除了奇偶性不同的状态转换得到，还可以是自身。

这个状态非常简单，比赛的时候我没有想到，确实还有很大的差距。

五、最后

这次比赛还是比较简单的。
前两道题是签到题，第三题背包，第四题状态，都不算太难。

不过第四题状态比较多，如果一个个写条件判断，可能代码量会很大。
这里使用位运算进行计算，代码量就少了好多。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号： tiankonguse
公众号 ID： tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。