leetcode 第 468 场算法比赛
作者: | 更新日期:
二分线段树 VS 区间树
本文首发于公众号:天空的代码世界,微信号:tiankonguse
零、背景
这次比赛前面两道题非常简单,第三题是暴力 BFS,第四题是二分套二分线段树,代码量比较大。
A: 循环
B: 贪心
C: BFS
D: 二分线段树、区间树
代码地址: https://github.com/tiankonguse/leetcode-solutions
一、偶数的按位或运算
题意:给你一个整数数组 nums。
返回数组中所有 偶数 的按位 或 运算结果。
如果 nums 中没有偶数,返回 0。
思路:按题意循环计算。
for (auto v : nums) {
if (v % 2 == 0) {
ans |= v;
}
}
二、最大子数组总值 I
题意:给定一个长度为 n 的整数数组 nums 和一个整数 k。
选择 k 个可以重复的子数组,使得这些子数组的值之和最大。
子数组值的定义:数组的最大值减去数组的最小值。
思路:贪心
子数组可以重复,直接对值最大的子数组选择 K 次即可。
值最大时,子数组包含最大值和最小值。
故计算最大值和最小值,即可计算出最大值。
ll maxVal = *max_element(nums.begin(), nums.end());
ll minVal = *min_element(nums.begin(), nums.end());
return (maxVal - minVal) * k;
三、拆分合并数组
题意:给你两个长度为 n 的整数数组 nums1 和 nums2。
你可以对 nums1 执行任意次下述的 拆分合并操作,返回将 nums1 转换为 nums2 所需的 最少拆分合并操作 次数。
操作:
1)选择一个子数组并删除
2)剩余的前后缀组成新的数组
3)删除的数组插入到新的数组的任意位置。
思路:BFS
数据范围只有 6,任意操作后最多有 6!=720 种结果。
故可以暴力 BFS 求解答案。
状态压缩:对于一个大小为 n 的数组,可以离散化到数字 1 到 n,然后 hash 拼接为一个 n 位十进制数字。
这样就可以使用一个数字代表一个数组了。
题意的原始操作是选择一个区间,删除后然后插入新的位置。
搜索时,需要枚举删除区间的起始位置和区间长度,然后枚举插入位置,每轮搜索会产生 O(n^3)个新状态。
分析删除与插入操作,可以发现等价于选择两个相邻区间,进行交换。
故可以精确计算出有 C(n+1, 3)个新状态。
queue<int> que;
memset(vis, 0, sizeof(vis));
Add(start, 1);
while (!que.empty()) {
const int v = que.front();
que.pop();
int step = vis[v];
for (int l = 0; l < n; l++) { // [l, mid) [mid, r)
for (int mid = l + 1; mid < n; mid++) {
for (int r = mid + 1; r <= n; r++) {
const int newVal = CalNextVal(v, l, mid, r);
Add(newVal, step + 1);
if (newVal == target) {
return step;
}
}
}
}
}
数字的相邻若干位进行交换,可以通过数学运算,O(1)完成。
auto CalNextVal = [&](int v, int l, int mid, int r) {
const int lm = mid - l, lr = r - mid;
const int lowVal = v % base[mid] / base[l];
const int highVal = v % base[r] / base[mid];
const int newVal = v - lowVal * base[l] - highVal * base[mid] + lowVal * base[l + lr] + highVal * base[l];
return newVal;
};
四、最大子数组总值 II
题意:给定一个长度为 n 的整数数组 nums 和一个整数 k。
选择 k 个不可以重复的子数组,使得这些子数组的值之和最大。
子数组值的定义:数组的最大值减去数组的最小值。
思路:二分线段树
思考一个问题:大小为 n 的数组最多会产生 C(n+1, 2)个子数组,不同的差值会有多少个呢?
初步猜想时,虽然值域很大,但是由于某些性质,不同的差值个数不会很多。
基于这个猜想,可以想到一个暴力解法:找到 TOP 的不同差值与个数,使得个数和不小于 K。
这里分为两个步骤:
1)找到下一个次大值
2)计算次大值的个数
这两个步骤都无法直接计算得到,但是通过通过前缀和来计算得到。
前缀和函数:差值大于等于 d 的子数组个数。
假设当前大于等于差值 D 的个数已经统计了,为 sum 个。
如果下个差值为 d,则可以证明,区间 (d,D)内的差值是不存在的。
故,可以二分找到下个差值 d 和前缀和,然后减去上个差值的前缀和,就是当前差值的个数。
vector<pair<ll, ll>> topK;
topK.reserve(k + 1);
ll maxVal = *max_element(nums.begin(), nums.end());
ll minVal = *min_element(nums.begin(), nums.end());
topK.push_back({maxVal - minVal + 1, 0}); // 构造一个虚拟的差值
// 二分找到小于 topK.back() 的最大值以及个数
ll sum = 0;
while (sum < k) { //
const ll preVal = topK.back().first; // 当前大于等于 preVal 的区间有 sum 个
ll r = preVal, l = 0; // [l, r)
while (l < r) {
ll mid = (l + r) / 2;
if (Check(mid, sum) > sum) {
l = mid + 1;
} else {
r = mid;
}
}
ll nowVal = l - 1;
ll nowNum = Check(nowVal, __LONG_LONG_MAX__);
topK.push_back({nowVal, nowNum - sum});
sum = nowNum;
}
差值都找到了,然后依次计算和即可。
ll ans = 0;
sum = 0;
for (auto [val, num] : topK) {
if (sum + num <= k) {
ans += val * num;
sum += num;
} else {
ans += val * (k - sum);
break;
}
}
return ans;
现在只剩一个问题:如何找大于等于 D 的差值个数。
很容易想到,枚举每个值当做最小值,计算出覆盖这个最小值的子数组中,有多少个子数组满足要求,累计求和即可。
此时会遇到一个问题:子数组之间存在重叠,如何避免重复统计。
这时候需要对子数组进行定义分类,使得每个子数组的最小值和最大值是确定的。
最小值定义 minP:最左边的最小值。
最近最大值定义 maxP :如果左边存在某个位置与最小值的差值大于等于 D,则最近最大值为最小值左边最后一个满足要求的位置。否则,在最小值右边找到第一个满足要求的位置。
则称这个子数组归属于 <minP, maxP>。
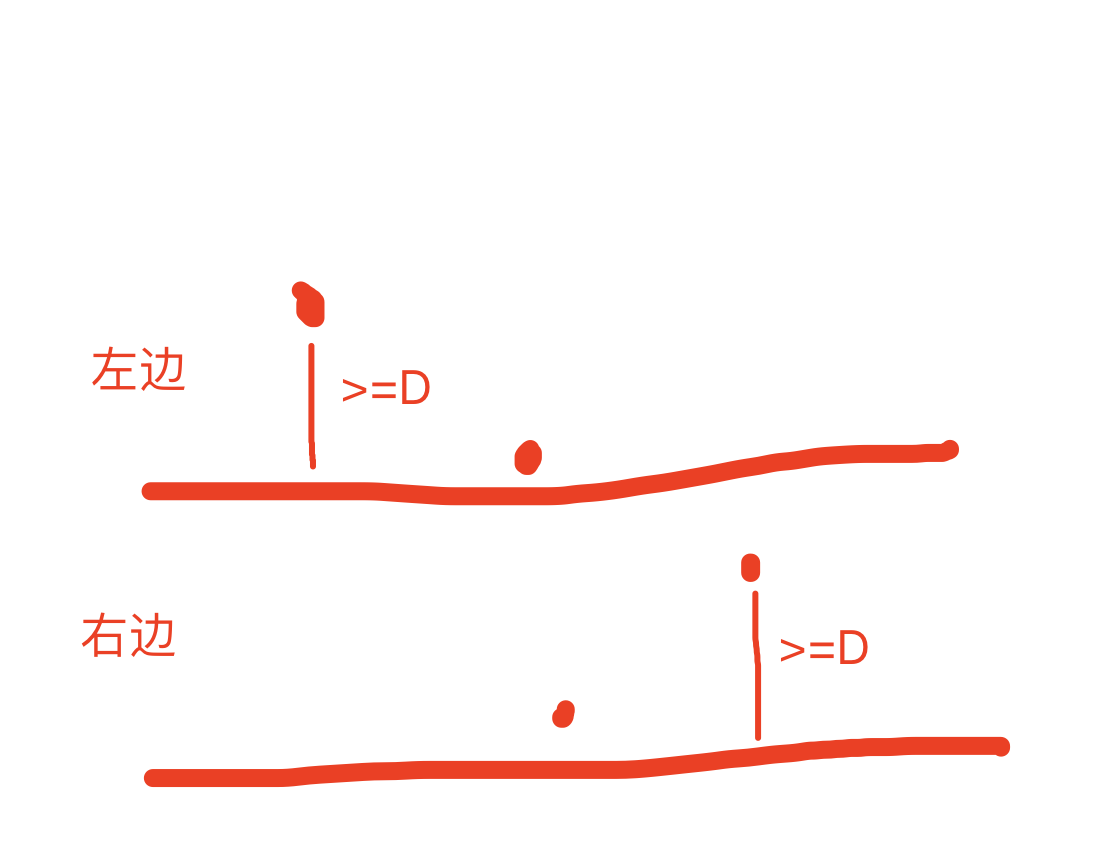
假设子数组 [l,r] 归属于 <minP, maxP>。
若 l-1的值大于 minP的值,则 [l-1, r] 也归属与 <minP, maxP>。
若 r+1的值大于等于 minP的值,则 [l, r+1] 也归属与 <minP, maxP>。
假设 l 前面直到 L 都满足要求,r 后面直到 R 都满足要求,则共有 (l - L + 1) * (R - r + 1)个子数组都归属于 <minP, maxP>。
每个位置向左与向右最远的延伸位置是确定的,故可以预处理出来。
vector<int> sta;
sta.reserve(n);
leftLast.resize(n + 1);
leftMax.resize(n + 1);
for (int i = 1; i <= n; i++) { // 从左到右, 单调递增栈,等于时按左边的小于右边的
while (!sta.empty() && nums[sta.back() - 1] > nums[i - 1]) {
sta.pop_back();
}
if (sta.empty()) { // 当前是最小值
leftLast[i] = 1;
} else {
leftLast[i] = sta.back() + 1;
}
sta.push_back(i);
leftMax[i] = segTree.QueryMax(leftLast[i], i);
}
到这里就可以做这道题了。
枚举每个最小值时,先尝试在左边找到最近最大值,然后判断向左与向右分别最远可以到哪里,从而计算出归属于左边的子数组个数。
最近的最大值,可以线段树+二分来做。
ll leftFirst = leftLast[i]; // 默认都可以随意选择
if (leftMax[i] - minVal >= d) { // 左边存在答案
int L = leftLast[i], R = i; // 找到区间内 [l, r) 最后一个满足大于等于 minVal+d 的位置
while (L < R) {
int mid = (L + R) / 2;
if (segTree.QueryMax(mid, i) - minVal < d) {
R = mid;
} else {
L = mid + 1;
}
}
leftFirst = R; // 如果左边存在答案,则更新找到第一个位置
const ll p = R - 1; // [R-1, i] 是最小的答案
num += (p - leftLast[i] + 1) * (rightLast[i] - i + 1);
if (num > minNum) {
return num;
}
}
左边的 <minP, maxP>没有任何限制,但是右边的需要加一个规则,来避免重复统计。
什么时候会重复统计呢?
一个子数组的最小值左右都存在最近最大值时。
故,右边进行统计时,左边界不能超过左边最近最大值位置,这个位置储存在上面代码的 leftFirst中。
这样,就可以通过这道题了。
最后,再来看下猜想是否成立吗,是否可以构造出一个数据,使得每个差值只有1个子数组,从而使得复杂度退化为 O(k*log(v)*n*log(n))。
什么时候差值会很多呢?
如果所有值是有序的,且差值也不同时,差值会最多。
此时数组是严格升序的,且下一个最大值与前面的所有值相减得到的差值,之前都没出现过。
很容易想到,这个序列满足 f(n)=2*f(n-1)+1。
得到的前缀差值如下:
0: 0
1: 0, 1
3: 0, 2, 3
7: 0, 4, 6, 7
15: 0, 8, 12, 11, 15
...
可以发现,差值有很多空洞,只需要 log(V)个数字,构造出 log(V)^2个差值。
所以可以想到一个新的序列:缺少哪个差值就补上哪个差值。
序列公式 f(n) = f(n-1) + min Val
0: 0
1: 0, 1
3: 0, 2, 3
7: 0, 4, 6, 7
12: 0, 5, 9, 11, 12
20: 0, 8, 13, 17, 19, 20
30: 0, 10, 18, 23, 27, 29, 30
44: 0, 14, 24, 32, 37, 41, 43, 44
59: 0, 15, 29, 39, 47, 52, 56, 58, 59
75: 0, 16, 31, 45, 55, 63, 68, 72, 74, 75
...
很神奇,这个序列竟然几乎没有重复值,上面的例子中只有 29 是重复的。
每新增一个值,就可以产生 O(n)个差值,值域最大是10^9,故大概3*10^4个数字,就可以构造出 10^9个差值。
基于这个规则,暴力计算一番,发现确实可以构造出一个反例,使得差值比较分散,从而使得复杂度降低为 O(n^2)。
例如值域不大于 10^9,只需要 22377 个数字,就可以构造出 212251636 个差值。
n=21000 v=877143324 d=186812366 minVal=86223 maxNum=7
n=21100 v=885785484 d=188605869 minVal=86622 maxNum=6
n=21200 v=894469639 d=190408436 minVal=87086 maxNum=6
n=21300 v=903198546 d=192218484 minVal=87509 maxNum=6
n=21400 v=911973116 d=194037672 minVal=87960 maxNum=7
n=21500 v=920791615 d=195864332 minVal=88400 maxNum=5
n=21600 v=929652827 d=197698774 minVal=88826 maxNum=5
n=21700 v=938556388 d=199542577 minVal=89255 maxNum=5
n=21800 v=947506914 d=201394764 minVal=89754 maxNum=5
n=21900 v=956503941 d=203255768 minVal=90210 maxNum=5
n=22000 v=965547341 d=205126045 minVal=90637 maxNum=6
n=22100 v=974634594 d=207004150 minVal=91122 maxNum=6
n=22200 v=983770053 d=208891217 minVal=91579 maxNum=5
n=22300 v=992951125 d=210786547 minVal=92033 maxNum=5
n=22377 v=1000051620 d=212251636 minVal=92407
回头看下前几名的代码,都使用的区间树。
具体来说是找到一种访问区间的顺序,从而可以每次得到下个次大值。
这个访问顺序属于贪心,即可以证明,如果一个区间 A 是区间 B 的子区间,则 A 的值肯定不大于 B 的值。
基于这种贪心,可以画出一个 DAG 图,然后通过优先队列不断地得到一个最大值,然后加入两个儿子。
加入儿子子数组时,需要计算子数组的值,这个可以使用线段树、RMQ、ST 来求最值都行。
复杂度:O(k log(k) log(n))

五、最后
这次比赛最后一题我只想到一直暴力的方法,没想到居然水过去了。
标准做法是区间树,之前没做过这类题,没想到区间树还有这个性质,挺有意思的。
《完》
-EOF-
本文公众号:天空的代码世界
个人微信号: tiankonguse
公众号 ID: tiankonguse-code
本文首发于公众号:天空的代码世界,微信号:tiankonguse
如果你想留言,可以在微信里面关注公众号进行留言。
