CSP-S 2020 编程算法比赛

零、背景

最近我计划研究 CSP-J 与 CSP-S 的比赛题目，之前已经完成了 9 场比赛的题解，今天将分享 2020 年 CSP-S 第二轮编程算法比赛的详细题解。

A: 模拟
B: 位运算
C: DAG 与嵌套表达式展开
D: 贪心博弈

代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/other/CSP-S/

比赛题目分类与题解
CSP-J 2024 题解 A:扑克牌入门 B: 地图探险普及− C: 小木棍普及/提高− D: 接龙提高+/省选−
CSP-S 2024 题解 A:决斗普及− B: 超速检测普及+/提高 C: 染色提高+/省选− D: 擂台游戏 NOI/NOI+/CTSC
CSP-J 2023 题解 A:小苹果普及− B: 公路普及− C: 一元二次方程普及/提高− D: 旅游巴士普及+/提高
CSP-S 2023 题解 A:密码锁普及− B: 消消乐提高+/省选− C: 结构体提高+/省选− D: 种树提高+/省选−
CSP-J 2022 题解 A:乘方入门 B: 解密普及− C: 逻辑表达式普及+/提高 D: 上升点列普及/提高−
CSP-S 2022 题解 A:假期计划提高+/省选− B: 策略游戏普及+/提高 C: 星战省选/NOI− D: 数据传输省选/NOI−
CSP-J 2021 题解 A:分糖果普及− B: 插入排序普及/提高− C: 网络连接普及/提高− D: 小熊的果篮普及+/提高
CSP-S 2021 题解 A:廊桥分配普及+/提高 B: 括号序列提高+/省选− C: 回文普及+/提高 D: 交通规划省选/NOI−
CSP-J 2020 题解 A:优秀的拆分入门 B: 直播获奖普及− C: 表达式普及+/提高 D: 方格取数普及+/提高
CSP-S 2020 题解 A:儒略日普及+/提高 B: 动物园普及/提高− C: 函数调用提高+/省选− D: 贪吃蛇 NOI/NOI+/CTSC

一、儒略日

题意：给一个日历规则，公元 1582 年 10 月 4 日之前按儒略历计算年月日，公元 1582 年 10 月 15 日之后按格里高利历计算年月日，中间的天数不存在。
假设公元前 4713 年 1 月 1 日是第 1 天，问给你一个年月日，是第几天。

儒略历：4年闰月一次。
格里高利历：4年闰月一次，100年不闰月，400年闰月。

思路：模拟

1600 年之前的年份，数据量不大，可以预处理每一年1月1日是第几天，储存在数组中。

while (p < Y1582) {  // -4712年 ~ 1581年
  ll oneDay = D365;
  if (p % 4 == 0) {
    oneDay++;
  }
  mp[day] = p;  // p 年1月1日，是第 day 天
  day += oneDay;
  p++;
}

mp[day] = p;       // 1582 年 1 月 1 日，是第 day 天
day += D365 - 10;  // 有 10 天不存在
p++;
while (p < 1600) {  // 1583 年 ~ 1599 年
  ll oneDay = D365;
  if (p % 400 == 0 || (p % 4 == 0 && p % 100 != 0)) {
    oneDay++;
  }
  mp[day] = p;  // p 年1月1日，是第 day 天
  day += oneDay;
  p++;
}

1600 年之后的，400年一个周期，只需要再预处理 400年每一年1月1日是第几天，储存起来。

offfsetDayY400.reserve(400);
ll offsetDay = 0;
for (int i = 0; i < 400; i++) {
  offfsetDayY400.push_back(offsetDay);
  offsetDay += D365;
  if (i % 400 == 0 || (i % 4 == 0 && i % 100 != 0)) {
    offsetDay++;
  }
}

查询时，先判断是否在 1600 年之前。
如果在之前，直接二分查找确定具体年份，然后根据是否是闰年，计算是几月几日。

if (r < day) {  // 1600 年之内的，需要二分查找
  auto it = mp.upper_bound(r);
  it--;
  auto [itDay, itYear] = *it;
  if (itYear < Y1582) {
    ll leftDay = r - itDay;
    const vector<pair<ll, ll>>& yearDay = (itYear % 4 != 0) ? yearNormal : yearLeap;
    auto [month, day] = yearDay[leftDay];
    return make_tuple(itYear, month, day);
  } else if (itYear == Y1582) {
    ll leftDay = r - itDay;
    const vector<pair<ll, ll>>& yearDay = year1582;
    auto [month, day] = yearDay[leftDay];
    return make_tuple(itYear, month, day);
  } else {
    ll leftDay = r - itDay;
    const vector<pair<ll, ll>>& yearDay =
        (itYear % 400 == 0 || (itYear % 4 == 0 && itYear % 100 != 0)) ? yearLeap : yearNormal;
    auto [month, day] = yearDay[leftDay];
    return make_tuple(itYear, month, day);
  }
}

如果在之后，根据剩余的天数计算有多少个 400年周期，以及剩余的天数。
之后二分查找，确定在400年具体第几年，然后根据是否是闰年，计算是几月几日。

ll leftDay = r - day;
ll itYear = p;
if (leftDay > Y400) {
  ll num = leftDay / Y400;
  itYear += num * 400;
  leftDay -= num * Y400;
}

auto it = upper_bound(offfsetDayY400.begin(), offfsetDayY400.end(), leftDay);
it--;
ll yearNum = it - offfsetDayY400.begin();
itYear += yearNum;
leftDay -= *it;
const vector<pair<ll, ll>>& yearDay =
    (itYear % 400 == 0 || (itYear % 4 == 0 && itYear % 100 != 0)) ? yearLeap : yearNormal;
auto [month, day] = yearDay[leftDay];
return make_tuple(itYear, month, day);

小技巧：平年和闰年天数和日期的关系可以提前预处理好，这样就可以是输入天数得到月份和日期。

const ll normalMonth[12] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const ll leapMonth[12] = {31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
for (int m = 0; m < M12; m++) {
  for (int d = 1; d <= normalMonth[m]; d++) {
    yearNormal.push_back({m + 1, d});
  }
}
for (int m = 0; m < M12; m++) {
  for (int d = 1; d <= leapMonth[m]; d++) {
    yearLeap.push_back({m + 1, d});
  }
}
for (int m = 0; m < M12; m++) {
  for (int d = 1; d <= normalMonth[m]; d++) {
    if (m + 1 == 10 && d == 5) {
      d = 15;  // 10月5日~10月14日不存在
    }
    year1582.push_back({m + 1, d});
  }
}

二、动物园

题意：给 n 个动物和一个条件列表：如果存在一个动物第 i 位为 1，则购买第 i 位的饲料，否则不购买第 i 位饲料。
根据当前的动物，确定了饲料集合。
问在不改变饲料集合的前提下，还能加入多少个动物。

思路：二进制

题目比较绕，不容易理解。

分析条件列表，可以发现二进制分为三类：
1）位数列表中存在，动物对应的位数为1，则购买该位饲料。
2）位数列表中存在，动物对应的位数为0，不购买该位饲料。 3）位数列表中不存在，动物对应的位数值不做要求，加入这个位数不影响饲料集合。

根据上面的分析，可以确定，新加入的动物不能与第二个规则冲突。
故需要统计，命中第二个规则的位数，剩余的其他位则都是可以存在的。

故这道题可以分三步来做：

第一步：统计当前动物的位数

ull mask = 0;
for (int i = 0; i < n; i++) {
  ull x;
  scanf("%llu", &x);
  mask |= x;
}

第二步：统计第二个规则的位数。

ull umask = 0;
for (int i = 0; i < m; i++) {
  int p;
  ull q;
  scanf("%d%llu", &p, &q);
  if ((mask & (1ULL << p)) == 0) {
    umask |= (1ULL << p);
  }
}
int bit = 0;
for (int i = 0; i < k; i++) {
  if (umask & (1ULL << i)) {
    bit++;
  }
}

第三步：计算可以加入的动物数。

由于数字最大可能为 1<<64，故这里使用 int128代替。

__int128_t ans = 1;
for (int i = 0; i < k - bit; i++) {
  ans *= 2;
}
ans -= n;
string str = MyToString(ans);
printf("%s\n", str.c_str());

三、函数调用

题意：有一个数组，有三类函数，问执行一个函数列表后，最终数组的值是多少。

函数1：指定位置加上一个值。
函数2：所有位置乘以一个值。
函数3：依次调用若干个其他函数。

思路：DAG 与嵌套表达式展开

题目已经说了函数不存在循环调用，所以调用链是一个 DAG 函数。

每个函数相当于一个表达式，整个 DAG 相当于嵌套表达式。

只看一个位置，嵌套表达式大概是下面的形式

((x*a*b+c)*d*e + f)*g*h...

嵌套表达式去除括号展开，大概如下

x*a*b*c*d*e*f*g*h... + c*d*e*g*h... + f*g*h...

总结下规律，对于每个函数1，需要乘以后面的所有函数2。

假设 DAG 是一个树，则可以逆序遍历树，累计所有乘积，从而计算出函数1需要加的值，从而计算出每个位置的值。

如果 DAG 是一个图，则同一个函数会被调用多次，从而导致函数1 有多个乘积，需要累加。

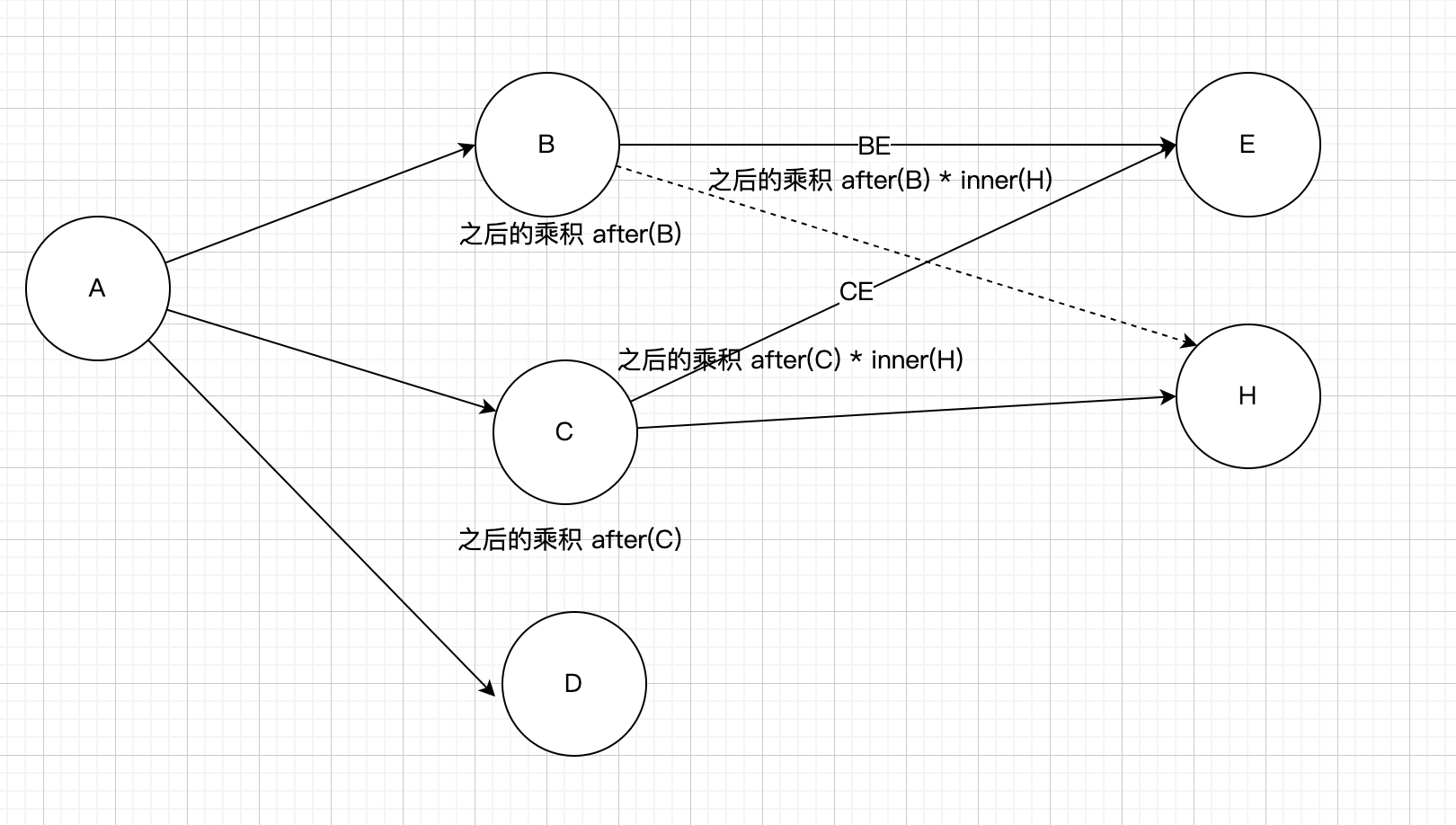
如上图，给每个顶点和每个边定义一个概念，叫做之后的乘积。

例如函数 A 是依次调用函数 B、C、D。
表达式展开时，函数 C 需要乘以函数 D 的所有乘积，这里记作为 after(C)。
一个函数内部有多个函数调用，一个叶子节点内部累计的乘积，记作inner(H)。

函数 C 调用函数 E 时，之后的乘积是after(C)*inner(H)。
函数 B 调用函数 E 时，之后的乘积是 after(B)*inner(H)。

此时，对于函数 E 来说，之后的乘积是 after(C)*inner(H) + after(B)*inner(H)。
即对于有多个入边的 DAG，需要累加所有来源顶点的乘积。

基于这个逻辑，先进行 DAG 拓扑排序，然后逆序遍历 DAG 计算每个顶点的乘积即可。

拓扑排序需要维护入度的个数，入度为0时就可以随时选择了。

void TopologicalSort() {
  orderedIndex.reserve(m + 1);
  orderedIndex.push_back(0);  // 0 是询问，也是根节点
  queue<int> que;
  for (int i = 1; i <= m; i++) {
    if (inDeg[i] == 0) {
      que.push(i);
    }
  }
  while (!que.empty()) {
    const int u = que.front();
    que.pop();
    orderedIndex.push_back(u);

    for (const auto v : G[u]) {
      inDeg[v]--;
      if (inDeg[v] == 0) {
        que.push(v);
      }
    }
  }
}

内部的乘积，可以由底往上，与拓扑排序相反的顺序来计算。

void CalNodeMul() {  // 计算每个节点自身的累计乘积
  for (int i = m; i >= 0; i--) {
    const int u = orderedIndex[i];
    for (const auto v : G[u]) {
      innerMul[u] = (innerMul[u] * innerMul[v]) % mod9;
    }
  }
}

之后的乘积，则按照拓扑排序的顺序访问节点，节点内也累计计算出节点子树内的之后乘积。

vector<ll> afterMul;  // 计算每个节点后续的乘积
void calNodeCount() {
  afterMul.resize(m + 1);
  afterMul[0] = 1;
  for (int i = 0; i <= m; i++) {
    const int u = orderedIndex[i];
    ll cnt = afterMul[u];  // 处理到 u, 说明所有依赖 u 的节点都处理完了
    for (const auto v : G[u]) {
      afterMul[v] = (afterMul[v] + cnt) % mod9;
      cnt = (cnt * innerMul[v]) % mod9;
    }
  }
}

最后的查询其实也可以当做一个函数，这样跑完 DAG，答案就出来了。

for (int i = 1; i <= n; i++) {
  A[i] = A[i] * innerMul[0] % mod9;
}
for (int i = 1; i <= m; i++) {
  if (P[i]) {  // 操作1，需要进行累加
    const int u = P[i];
    A[u] = (A[u] + V[i] * afterMul[i]) % mod9;
  }
}
for (int i = 1; i <= n; i++) {
  printf("%lld%c", A[i], i < n ? ' ' : '\n');
}

四、贪吃蛇

题意：n 个有体力值的蛇按顺序排列，如果体力数值相等，则按编号大的体力值更高。
每条蛇都很聪明，问在自己不被吃掉并尽可能的吃其他蛇时，最终剩余几条蛇。

前提：选择体力值最大的蛇 A 与体力值最小的蛇 B。
选择1：A 吃掉 B，此时 A 的体力值需要减去 B 的体力值，之后继续游戏。
选择2：A 不吃 B，游戏结束。

思路：贪心与博弈。

原始题目很难理解，上面是简化后的，就容易理解多了。

分析最大值和最小值的关系。

如果只有两个蛇，显然吃掉是没问题的。
如果有三个蛇 A < B < C，则需要看吃掉之后 C-A 与另外一个蛇 B 的关系。
如果 C-A > B，则可以吃掉 B，否则就会被吃，此时不能吃 A。

如果有四个蛇 A < B < C < D，则需要看吃掉之后 D-A 与另外一个蛇 B 的关系。

如果 D-A > B，则剩余蛇的关系是 B < D-A < C。
由于 A < B < C < D,可以推导出 C-B < D-A。
即 C 吃掉 B 时，依旧在 D-A 前面，会被 D 吃掉。
所以 C 此时的最优选择是不吃 B，游戏结束。

由此可以得出一个结论：体力值最大的蛇减去体力值最小的蛇后，如果结果不是体力值最小的蛇，则可以果断选择吃掉，自己肯定不会被吃掉。

如果是最小值呢，则关系是 D-A < B < C。
此时决定权交到了 C 的手上。
如果 C 选择吃，且 C自己不会被吃，则 C肯定会选择吃。此时D会被吃掉，故 D就不能选择吃掉 A。
如果 C 选择吃之后，C之后也会被吃掉，则 C肯定选择不吃，此时 D就存活下来，故 D可以果断选择吃 A。

这里 C 会不会被吃掉，和 D 会不会被吃掉是等价的，故是一个递归博弈问题。
不管怎么选择，进入博弈状态后，最多只会吃1条蛇了。

故，可以先贪心在保证不被吃的前提下（吃之后不是最小值），尽可能的吃蛇。
之后，进行博弈递归，判断是否可以再吃一条蛇。

deque<pair<ll, ll>> que[2];

ll ans = 0;
while (que[0].size() + que[1].size() >= 3) {  // 必吃
  auto [maxVal, maxIdx, maxType] = GetMax();
  auto [minVal, minIdx, minType] = GetMin();
  auto [secondMinVal, secondMinIdx, secondMinType] = GetMin();
  if (maxVal - minVal > secondMinVal || (maxVal - minVal == secondMinVal && maxIdx > secondMinIdx)) {
    que[1].push_front({maxVal - minVal, maxIdx}); // 先加入大的
    que[secondMinType].push_front({secondMinVal, secondMinIdx});
    ans++;
  } else { // 撤销操作
    que[secondMinType].push_front({secondMinVal, secondMinIdx});
    que[minType].push_front({minVal, minIdx});
    que[maxType].push_back({maxVal, maxIdx});
    break;
  }
}
if (que[0].size() + que[1].size() == 2) {
  ans++;
} else {  // 可能不吃
  if (StartGame()) {
    ans++;
  }
}
return ans;

博弈游戏的代码与贪心的代码很类似。
必胜时游戏结束，否则尝试吃掉，然后递归判断自己会不会被吃。

bool StartGame() {  // 最小值是否被吃
  int leftNum = que[0].size() + que[1].size();
  if (leftNum <= 1) return false;
  if (leftNum == 2) return true;  // 被吃
  auto [maxVal, maxIdx, maxType] = GetMax();
  auto [minVal, minIdx, minType] = GetMin();
  auto [secondMinVal, secondMinIdx, secondMinType] = GetMin();
  if (maxVal - minVal > secondMinVal || (maxVal - minVal == secondMinVal && maxIdx > secondMinIdx)) {
    return true;
  }
  que[secondMinType].push_front({secondMinVal, secondMinIdx});
  que[1].push_front({maxVal - minVal, maxIdx});
  return !StartGame();
}

优化：你可能注意到，上面的代码直接从双向队列中获取最大值和最小值。

这个可以证明，不断贪心吃的时候，新产生的蛇的体力值是递减的。
证明也很简单，由于 A < B < C < D 可以推导出 C-B < D-A，因此后面吃的蛇小于前面吃的蛇。

当然，你可能会想，会不会若干轮下来，最小值在新的队列里呢？
这是不可能的，因为根据前面的贪心要求，加入新队列的值不是最小的，即旧队列肯定存在更小的值。

如果旧队列只剩一个最小值，吃之后，会不会需要插入到中间位置呢？
也不会，因为此时吃之后剩余的必定是最小值，不再满足贪心规则。

因此，可以通过贪心加博弈的方法来解决这个问题。

五、最后

这次比赛难度比较大，第三题 DAG 与嵌套表达式展开，不容易思考。
第四题贪心就不容易想到，博弈更不容易想到，难度定位为黑题也是没问题的。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。