CSP-J 2019 编程算法比赛

零、背景

最近我计划研究 CSP-J 与 CSP-S 的比赛题目，之前已经完成了 10 场比赛的题解，今天将分享 2019 年 CSP-J 第二轮编程算法比赛的详细题解。

A: 循环
B: 离散化+二分+线段树
C: 完全背包
D: 单源最短路

代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/other/CSP-J/

比赛题目分类与题解
CSP-J 2024 题解 A:扑克牌入门 B: 地图探险普及− C: 小木棍普及/提高− D: 接龙提高+/省选−
CSP-S 2024 题解 A:决斗普及− B: 超速检测普及+/提高 C: 染色提高+/省选− D: 擂台游戏 NOI/NOI+/CTSC
CSP-J 2023 题解 A:小苹果普及− B: 公路普及− C: 一元二次方程普及/提高− D: 旅游巴士普及+/提高
CSP-S 2023 题解 A:密码锁普及− B: 消消乐提高+/省选− C: 结构体提高+/省选− D: 种树提高+/省选−
CSP-J 2022 题解 A:乘方入门 B: 解密普及− C: 逻辑表达式普及+/提高 D: 上升点列普及/提高−
CSP-S 2022 题解 A:假期计划提高+/省选− B: 策略游戏普及+/提高 C: 星战省选/NOI− D: 数据传输省选/NOI−
CSP-J 2021 题解 A:分糖果普及− B: 插入排序普及/提高− C: 网络连接普及/提高− D: 小熊的果篮普及+/提高
CSP-S 2021 题解 A:廊桥分配普及+/提高 B: 括号序列提高+/省选− C: 回文普及+/提高 D: 交通规划省选/NOI−
CSP-J 2020 题解 A:优秀的拆分入门 B: 直播获奖普及− C: 表达式普及+/提高 D: 方格取数普及+/提高
CSP-S 2020 题解 A:儒略日普及+/提高 B: 动物园普及/提高− C: 函数调用提高+/省选− D: 贪吃蛇 NOI/NOI+/CTSC
CSP-J 2019 题解 A:数字游戏入门 B: 公交换乘普及− C: 纪念品普及+/提高 D: 加工零件普及+/提高

一、数字游戏

题意：给一个 01 字符串，问存在多少个 1。

思路：循环判断即可。

二、公交换乘

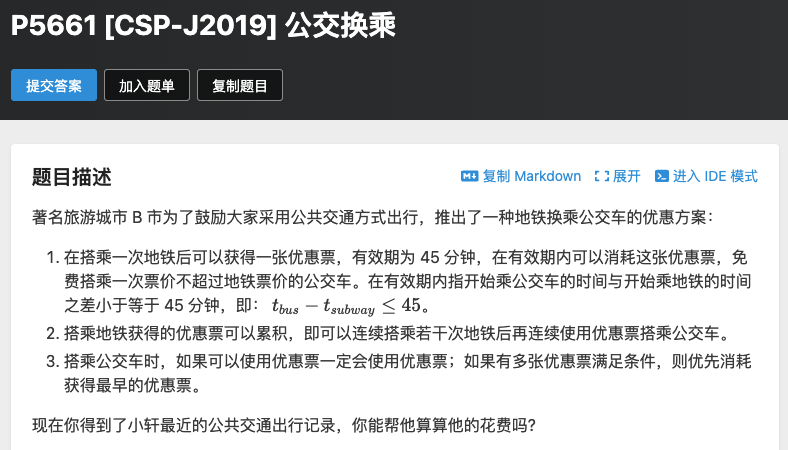
题意：有两种交通工具：地铁和公交。乘坐一次地铁可以得到一个优惠券， 45 分钟内可以免费乘坐一次票价不超过对应地铁的公交。
现在给出乘坐地铁和公交的时间表，问最终可以节省多少钱。

要求：地铁优惠券可以积攒，但优惠券必须按顺序抵扣公交费用。

思路：二分离散化线段树

要想免费乘坐公交，需要找到有效期内、尚未抵扣的、最早的、不小于公交价格的优惠券。

可以发现，有四个条件。

1）有效期内
2）未使用 3）不小于公交价格
4）最早的

有效期内代表数据结构需要支持区间搜索
未使用，数据结构需要支持更新操作，使用后需要进行删除。

而‘不小于且最早的’这一条件较为复杂，无法直接构造对应的数据结构，通常采用二分加线段树最大值来实现。

故，我们需要支持一个支持单点更新、区间查询最大值的线段树。

另外，时间比较大，故需要预处理进行离散化。

SegTree st;
st.Init(index);
st.Build();
ll ans = 0;
for (auto [type, price, time] : events) {
  ans += price;
  if (type == 0) {
    int t = h[time];
    st.Update(t, price);
  } else {
    int l = h[time - 45];
    int r = h[time];
    if (st.QueryMax(l, r).first >= price) {  // 区间内存在一个价格大于等于price的物品
      while (l < r) {                        // [l, r)
        int mid = (l + r) >> 1;
        if (st.QueryMax(l, mid).first >= price) {
          r = mid;
        } else {
          l = mid + 1;
        }
      }
      ans -= price;  // 免费
      st.Update(l, -st.QueryMax(l, l).first);
    }
  }
}
printf("%lld\n", ans);

三、纪念品

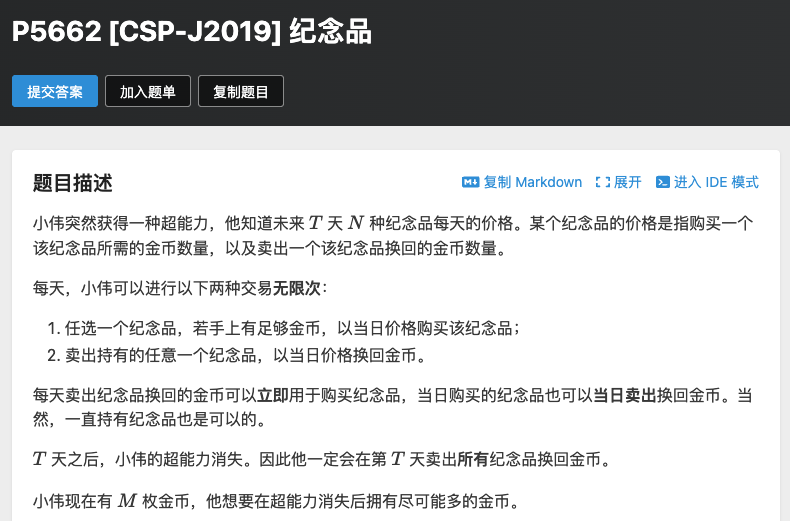
题意：我们知道未来 T 天每个股价的价格，第一天有 N 元，每天可以无限制地买卖，问如何买卖，才能使最后一天金钱最多。

思路：完全背包

由于可以无限制地买卖，每天的目标都是使金钱额度最大，因此前一天买入的股票会在第二天全部卖出，第二天到第三天时再重新买入与卖出。

因此，只需要分析两天之间如何买卖。
对于每个股票，可以无限买入，第二天卖出的价格当做收益，这个就是一个完全背包问题。

for (int i = 0; i < n; i++) {
  scanf("%d", &nums[0][i]);
}
int W = m;
for (int t = 1; t < T; t++) {
  const int now = t % 2, pre = (t - 1) % 2;
  memset(dp, 0, sizeof(int) * (W + 1));
  for (int i = 0; i < n; i++) {
    scanf("%d", &nums[now][i]);
    const int x = nums[pre][i], y = nums[now][i];  // 双Buf 滚动数组
    if (x < y) {
      const int w = x, val = y - x;
      for (int j = w; j <= W; j++) {  // 完全背包
        dp[j] = max(dp[j], dp[j - w] + val);
      }
    }
  }
  W += dp[W];
}
printf("%d\n", W);

四、加工零件

题意：工厂的供应链是一个有向图，一个节点进行第 K 阶段加工零件时，依赖所有相邻边的节点进行第 K-1 阶段预加工。
如果节点是第一阶段加工零件，则需要周围相邻边的节点的原材料。
现在问某个节点进行第 K 阶段加工零件时，是否需要第一个节点提供原材料。

思路：最短路

每个节点到达相邻节点时阶段数减一，如果依赖第一个节点的原材料，那么到达第一个节点时恰好是第 0 阶段。
如，如果询问节点存在到第一个节点的一个长度为 K 的路径，则第一个节点需要提供原材料。

假设到达第一个节点的最短路径是 K, 由于两个点之间可以来回传递，因此长度为 K+2n的路径也是可以到达的。

同样的，如果第一个节点可以到达一个奇数环，从而到达节点的最短路奇偶性发生翻转，假设代价是 M，则 M+2n 的长度也是可以到达的。

如何找到最小的M 呢？

可以将所有节点拆分为偶数路径节点和奇数路径节点，然后分别求每个节点的奇数和偶数路径的最短路。
询问时，先判断是奇数路径还是偶数路径，然后进行比较即可。

// 求 0 的单源最短路
vector<vector<int>> dis(2, vector<int>(n, -1));
queue<pair<int, int>> que;
auto Add = [&](int v, int flag, int step) {
  if (dis[flag][v] != -1) return;
  dis[flag][v] = step;
  que.push({flag, v});
};
Add(0, 0, 0);
while (!que.empty()) {
  const auto [flag, u] = que.front();
  que.pop();
  const int nextStep = dis[flag][u] + 1;
  for (auto v : g[u]) {
    Add(v, 1 - flag, nextStep);
  }
}
auto Check = [&](int v, int step) -> bool {
  int flag = step % 2;
  return dis[flag][v] != -1 && dis[flag][v] <= step;
};
while (q--) {
  ll A, L;
  scanf("%lld%lld", &A, &L);
  A--;
  printf("%s\n", Check(A, L) ? "Yes" : "No");
}

五、最后

这次比赛比较简单，不过作为 J 级别，第二题二分离散化线段树、第三题完全背包、第四题奇偶最短路，都需要稍微转化一下，对于这个级别，还是有一定的难度的。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。