历年 CSP-J CSP-S 题型总结之二分算法
作者: | 更新日期:
二分、线段树、动态规划、最短路
本文首发于公众号:天空的代码世界,微信号:tiankonguse
零、背景
CSP-J/S 是从 2019 年开始举办的。
之前已经在文章《近 6 年 CSP-J 算法题型分析》和《历年 CSP-S 算法题型分析》两篇文章里总计了 CSP-J 和 CSP-S 的题型。
接下来我的规划分两部分:
规划1:介绍常见算法如何实现,以及历年的真题中是如何应用的。
规划2:介绍面对比赛,使用什么样的策略,才能尽可能的得高分。
这里是规划1的第一篇文章,先介绍二分算法与真题解析。
一、算法介绍
二分算法分为两种。
一种是数据已经在有序列表或者有序集合里,进行二分查找。
另一种是需要对数轴区间进行二分,找到满足答案的位置。
针对第一种,我们可以直接使用 STL 的库函数。
常用的有 lower_bound 与 upper_bound。
lower_bound 的含义是在非降序序列中,找到第一个大于等于指定值的位置。
upper_bound 的含义是 在非降序序列中,找到第一个大于指定值的位置。
没找到时,指向最后一个元素的下个位置。
两个函数使用场景完全相同,所以下面只使用 lower_bound 来举例。
int arrList[] = {1, 2, 3, 4, 5};
int arrOffset= lower_bound(arrList, arrList + 5, 3) - arrList;
vector<int> vecList = {1, 2, 3, 4, 5};
int offset= lower_bound(vecList.begin(), vecList.end(), 3) - vecList.begin();
map<ll, ll> h = { {1, 2}, {3, 4}, {5, 6}, {7, 8}, {9, 10} };
auto it = h.lower_bound(5); // 不存在时等于 h.end()
set<int> s = {1, 2, 3, 4, 5};
auto it2 = s.lower_bound(3); // 不存在时等于 s.end()
针对第二种,需要自己实现二分代码。
这时候,建议大家按下面模版来写。
步骤1:定义左右边界 [l, r),左闭右开
步骤2:序列的值进行抽象,使得前半段都是0,后半段都是1
步骤3:封装判断函数 Check,判断是不是 1。
步骤4:二分代码的目标是找到第一个1的位置,不存在时为右边界。
步骤5:如果要找最后一个 0,答案减一即可。
基于上面步骤,二分代码固定写为下面的形式。
int l = 0, r = 100000; // [l, r)
auto Check = [&](const ll& mid)->bool { //
};
// 0 0 0 0 0 1 1 1 1 1
while (l < r) {
int mid = (l + r) >> 1;
if (Check(mid)) {
r = mid;
} else {
l = mid + 1;
}
}
if(r == 100000){
// 全是 0
}else{
// r 是第一个 1 的位置
// r-1 是最后一个 0 的位置
}
二、CSP-J 真题回顾
如下图,在《近 6 年 CSP-J 算法题型分析》文章中,我们可以注意到 6 年来二分题都是第二道题。
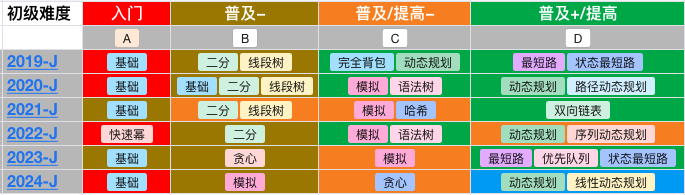
这个图不够清晰,所以转化为题型为列的表格,可以发现二分主要集中在第二列,即普及/提高−难度的上,有 4 次比赛出现过。
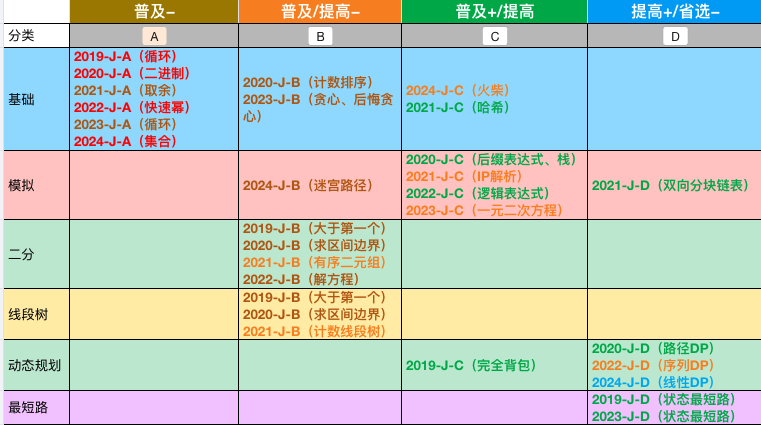
2019-J-B 的题目是 公交换乘。
题目要求要想免费乘坐公交,需要找到有效期内、尚未抵扣的、最早的、不小于公交价格的优惠券。
如果我们有一个数据结构可以做到区间查询最大值,则可以二分前缀区间,找到这个区间的边界,使得左半部都不满足,右半部都满足。
步骤1:确定区间边界,左边界是有效期的起始位置,右边界为当前时刻。
步骤2:将序列的值抽象为区间前缀是否存在答案,此时序列为 0 0 0 0 1 1 1 1 1
步骤3:封装 Check 函数,用相应的数据结构判断指定区间是否存在答案。
步骤4:使用上个小节介绍的固定二分模版代码,查找到一个分界线位置。
只要这个位置不是右边界,则找到一个最早的不小于公交价格的的优惠券。
2020-J-B 的题目是 直播获奖。
题目要求是每次查询时,需要找第 K 个数。
如果我们可以使用某个数据结构做到查询区间内的个数,则可以通过二分后缀区间,使得左半部个数大于 K 个,右半部不大于 K 个。
步骤1:在完整的题目区间范围内查询。
步骤2:序列的值抽象定义为后缀区间的个数是否大于K,此时序列为 1 1 1 1 0 0 0 0
步骤3:封装 Check 函数,使用对应的数据结构来判断指定的区间是否存在答案。
步骤4:使用上个小节介绍的固定二分模版代码,查询到一个位置。
这里肯定存在答案,故查找到的位置即为答案。
2021-J-B 的题目是 插入排序。
题目要求修改元素排序,问在第几名。
修改5000次,查询2万次,故可以暴力插入排序,询问时二分查询答案。
由于这里容器是有序的,直接使用 lower_bound 进行二分查找。
注:暴力修改时,也可以二分找到旧位置并删除,然后二分找到新位置插入。
2022-J-B 的题目是 解密。
题目转化一下,就是一个一元二次方程的整数求解,满足有序性,可以直接使用二分来找答案。
步骤1:左边界是 1, 右边界是对称轴。
步骤2:序列的值定义为方程是否小于0,左边在坐标轴下面小于0,右边在坐标值上面大于0,此时序列为 0 0 0 0 0 1 1 1 1
步骤3:封装 Check 函数,判断是否小于0。
步骤4:使用上个小节介绍的固定二分模版代码,查询到一个位置。
这里可能不存在答案,故找到位置后,需要带入方程,判断是否等于0, 不等于0 就没有整数解。
三、CSP-S 真题回顾
这里直接来看 CSP-S 题型为列的表格,可以发现二分题型比较分散,5次比赛每道题都出现过,不过主要还是集中在第一题。
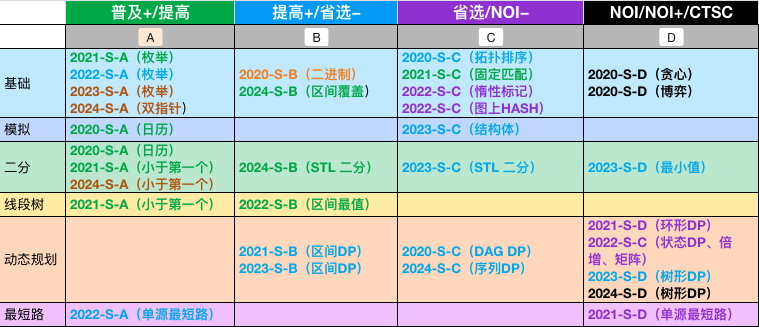
2020-S-A 的题目是 儒略日。
题目是指定一个日期当做第 1 天,问第几天是哪年哪月哪日。
由于闰年是400年一个周期,暴力的做法是预处理出400年的所有天数与日期的关系。
这样输入 400 年内的一个天数偏移量后,可以直接查表找到对应的日期。
我的做法是预处理三个表。
第一个是每年与天数的关系。
第二个是平年内日期与天数的关系。
第三个是闰年内日期与天数的关系。
这个时候,天数不是连续的,所以没法直接使用下标访问,只能使用二分找到具体的年,然后根据闰年或平年查对应的表即可。
2021-S-A 的题目是 廊桥分配。
题目要求一个飞机到达时,需要找到所有空廊桥的最小编号。
空廊桥代表廊桥里面的飞机的离开时间小于 t0。
即找到所有离开时间小于 t0 且编号最小的廊桥。
这个在 CSP-J 的时候已经做过两道类似的题了。
使用某个数据结构来查询区间最小值,结合二分,从而可以找到最小的编号。
2024-S-A 的题目是 决斗。
题目贪心转换之后,就是每个怪物可以杀死一个分数比自己低的怪物,问如何匹配,才能杀死最多的怪物。
如果做题的时候,如果没想到快慢指针,而是使用集合的方式去思考,就需要在集合里找到小于指定元素的最大值了。
这个可以直接使用集合的 lower_bound 来快速找到大于等于的位置,前一个就是不大于的位置了。
2024-S-B 的题目是 超速检测。
题目是综合型的,其中一步时,有很多摄像头和一个超速区间,问区间是否覆盖的有摄像头。
假设超速区间是 [a,b],问题就转化为了序列中大于等于 a 的元素,是否不大于 b。
所以只需要二分查找找到大于等于 a 的位置即可,直接使用 STL 的 lower_bound。
2023-S-C 的题目是 结构体。
这道题是一个模拟题。
每个结构体有很多成员,成员也可能是结构体,这是一个嵌套的过程。
所有成员都有一个地址,现在需要根据地址找到对应的成员。
这个可以理解为一个多叉树,叶子节点从左到右是有序的,父节点的编号是第一个儿子的编号。
现在需要快速找到叶子节点。
多叉树的儿子很多,但儿子的编号是有序的,所以在每一层二分找到查询地址属于哪个儿子,递归查询即可。
儿子储存在有序的容器里,所以可以直接使用 STL 的二分查找。
2023-S-D 的题目是 种树。
题目介绍了一个很复杂的规则,求最小值。
对于这种,典型的方法就是二分答案,判断是否满足规则,从而找到最小的答案。
四、总结
回顾一下所有真题,可以使用二分的题目共出现了 10 次。
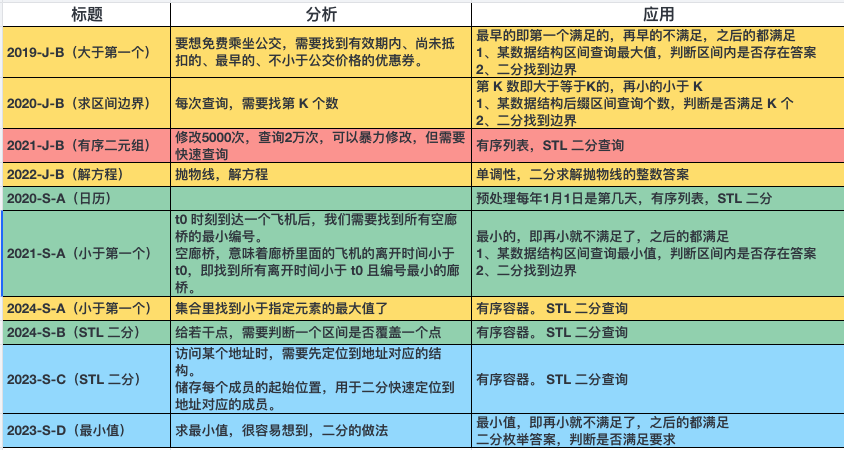
如上图,根据出现的场景,抽象一下,分为三类:
1)转化后是标准的有序容器,直接 STL 二分查找。
2)满足某些条件下的最小/大的,转化为左半部区间不满足,右半部区间满足即可。
2)抽象之后满足单调性,从而转化为左半部区间不满足,右半部区间满足。
二分算法的代码比较简单,所以这里重点分析了相关题目。
后面其他的算法,则会重点介绍算法,快速介绍真题的应用。
《完》
-EOF-
本文公众号:天空的代码世界
个人微信号:tiankonguse
公众号 ID:tiankonguse-code
本文首发于公众号:天空的代码世界,微信号:tiankonguse
如果你想留言,可以在微信里面关注公众号进行留言。
