CSP-J/S 备赛必学算法之线段树
作者: | 更新日期:
二分、线段树、动态规划、最短路
本文首发于公众号:天空的代码世界,微信号:tiankonguse
零、背景
CSP-J/S 是从 2019 年开始举办的。
之前已经在《近 6 年 CSP-J 算法题型分析》和《历年 CSP-S 算法题型分析》两篇文章里总结了 CSP-J 和 CSP-S 的题型。
接下来我的规划分两部分:
规划1:介绍常见算法如何实现,以及历年的真题中是如何应用的。
规划2:介绍面对比赛,使用什么样的策略,才能尽可能的得高分。
规划1的第一篇文章是二分,之前已经在《CSP-J/S 题型总结之二分》分享过了。
这里是规划1的第二篇文章,介绍线段树。
一、算法介绍
根据 NOI 大纲,CSP-J 阶段并不要求掌握线段树。
而 CSP-S 阶段要求理解其基本原理,包括单点更新与查询、区间更新与查询以及延迟标记(Lazy Propagation)。
需要注意的是,区间操作的实现通常依赖于延迟标记,而当区间大小为 1 时,区间操作自然退化为单点操作。
因此,如果能理解并实现区间更新的逻辑,就相当于掌握了 CSP-J/S 大纲中关于线段树的全部核心内容。
从本质上看,线段树(Segment Tree)是一种基于分治思想的二叉树结构,能将区间查询与区间更新的复杂度都降低到 O(log n)。
其中,每个节点代表一个区间 [l, r]:
叶子节点对应原始数组的单个元素(区间长度为 1);
非叶子节点存储子区间的聚合信息(如区间和、最大值等),其左右子区间分别为 [l, mid] 和 [mid + 1, r],其中 mid = (l + r) / 2。
节点的值通常由左右子节点的值合并而来,用于表示该区间的某种性质(如区间和、最值、最小值等)。
线段树适用于频繁区间操作的场景,常见应用包括:
1)区间求和 / 区间平均数:如统计数组某区间的和、平均值。
2)区间最值(最大值 / 最小值):如查询数组某区间的最大值(RMQ 问题,线段树是 RMQ 的解决方案之一)。
3)区间更新:如将某区间所有元素加 / 减一个值、乘 / 除一个值。
4)区间 GCD/LCM:如查询某区间的最大公约数(GCD)或最小公倍数(LCM)。
5)二维线段树:扩展到二维数组,处理矩形区域的查询与更新(如二维区间求和)。
线段树的存储方式
由于线段树是逻辑上的完全二叉树,实际实现中通常用数组(一维)存储,避免使用指针(简化代码)。
对于长度为 n 的原数组,线段树的数组大小需满足:
若 n 是 2 的幂,线段树数组大小为 2*n(叶子节点占 n 个,非叶子节点占 n-1 个,总 2n-1,取 2n 方便计算)。
若 n 不是 2 的幂,需找到大于 n 的最小 2 的幂(记为 m),线段树数组大小为 2*m(确保覆盖所有子区间)。
实际实现时,常直接取 4*n 作为线段树数组大小,因为 4*n 足够覆盖所有可能的节点数。
int maxNM; // 线段树区间 [1, maxNM]
vector<ll> sign; // 延迟标记
vector<pair<ll, int>> minVal; // 记录最值的位置
vector<pair<ll, int>> maxVal; // 记录最值的位置
vector<ll> sumVal; // 记录区间和
vector<pair<ll, ll>> ranges; // 节点对应的区间边界,方便快速计算区间和
vector<ll> str; // 原始数组的值,用于快速初始化
void Init(vector<int>& str_, const ll default_val = 0) {
maxNM = str_.size() + 1;
sign.resize(maxNM << 2, 0);
minVal.resize(maxNM << 2);
maxVal.resize(maxNM << 2);
sumVal.resize(maxNM << 2);
ranges.resize(maxNM << 2);
str.clear();
// default_val 初始值按需设置,一般是0,也可以按需设置为最大值或者最小值
str.resize(maxNM + 1, default_val);
for (int i = 0; i < str_.size(); i++) {
str[i + 1] = str_[i];
}
}
线段树的操作
线段树的核心操作围绕 “如何维护区间信息” 展开,主要包括建树、区间更新、区间查询三大类
建树是将原数组的信息递归填充到线段树中的过程,从根节点开始,逐步向下划分区间,直到叶子节点,再向上合并子节点的信息。
时间复杂度:O(n)
void Build(int l = 1, int r = maxNM, int rt = 1) {
sign[rt] = 0;
ranges[rt] = {l, r};
if (l == r) {
sumVal[rt] = str[l]; // 如果 str 没有复制一份,则需要注意边界是否越界
minVal[rt] = maxVal[rt] = {str[l], l};
return;
}
int m = (l + r) >> 1;
Build(l, m, rt << 1);
Build(m + 1, r, rt << 1 | 1);
PushUp(rt, l, r);
}
PushUp 用于合并子节点的信息。
// 合并函数,按需进行合并
void PushUp(int rt, int l, int r) {
minVal[rt] = min(minVal[rt << 1], minVal[rt << 1 | 1]);
maxVal[rt] = max(maxVal[rt << 1], maxVal[rt << 1 | 1]);
sumVal[rt] = sumVal[rt << 1] + sumVal[rt << 1 | 1];
}
更新时,从根节点开始,递归地更新左右子树,直到找到包含更新区间的节点。
需要更新的节点若更新至叶子节点,时间复杂度会退化为 O (n log(n)),效率极低。
因此引入懒标记,其核心思想是 “延迟更新”:只标记当前节点的区间需要更新,暂不递归更新子节点,直到后续操作(查询 / 更新)涉及子节点时,再将标记下推(Push Down),完成子节点的更新。
注:ranges 数组存储的是节点的左右边界,为了计算区间的大小,更新的时候可以快速计算区间和
int Num(pair<ll, ll> p) { return p.second - p.first + 1; }
void Update(int L, int R, ll add, int l = 1, int r = maxNM, int rt = 1) {
if (L <= l && r <= R) { // 覆盖更新区间
sign[rt] += add; // 延迟标记整体加 add
minVal[rt].first += add;
maxVal[rt].first += add;
sumVal[rt] += add * Num(ranges[rt]); // ranges 与 r - l + 1 等价
return;
}
PushDown(rt);
int m = (l + r) >> 1;
if (L <= m) Update(L, R, add, l, m, rt << 1);
if (R > m) Update(L, R, add, m + 1, r, rt << 1 | 1);
PushUp(rt, l, r);
}
下推延迟标记的过程是将延迟标记的值传递给左右子节点,并将延迟标记清零。 目的是为了避免重复计算,从而提高效率。
void PushDown(int rt) {
if (sign[rt]) {
sign[rt << 1] += sign[rt];
sign[rt << 1 | 1] += sign[rt];
minVal[rt << 1].first += sign[rt];
minVal[rt << 1 | 1].first += sign[rt];
maxVal[rt << 1].first += sign[rt];
maxVal[rt << 1 | 1].first += sign[rt];
sumVal[rt << 1] += sign[rt] * Num(ranges[rt << 1]);
sumVal[rt << 1 | 1] += sign[rt] * Num(ranges[rt << 1 | 1]);
sign[rt] = 0;
}
}
区间查询是获取某个目标区间 [L, R] 的聚合信息(如和、最值),通过递归判断当前节点区间与目标区间的交集,只访问必要的子节点,避免遍历所有节点。
下面是最大值的查询代码,最小值以及区间和的查询与下面的代码类似。
// L,R 查询的区间
// rt,l,r 线段树的节点编号与对应的区间
pair<ll, int> QueryMax(int L, int R, int l = 1, int r = maxNM, int rt = 1) {
if (L <= l && r <= R) {
return maxVal[rt];
}
PushDown(rt);
int m = (l + r) >> 1;
pair<ll, int> ret = {-1, 0};
if (L <= m) {
ret = max(ret, QueryMax(L, R, l, m, rt << 1));
}
if (m < R) {
ret = max(ret, QueryMax(L, R, m + 1, r, rt << 1 | 1));
}
return ret;
}
使用时,先初始化,然后更新与查询即可。
SegTree segTree;
vector<int> nums; // 原始数据
segTree.Init(nums, 0);
segTree.Build();
segTree.QuerySum(1, p); // 区间查询
// 单点设置值,由于更新是添加值,如果需要单点设置值,先查询出值,然后计算出差值,再更新
int addVal = val - segTree.QuerySum(p, p);
segTree.Update(p, p, addVal); // 区间更新
二、真题解析
如下图,是 CSP-J 历年真题的题型分布,其中有 3 道题可以使用基础算法解决,同时数据范围变大时,也可以使用线段树来解决。
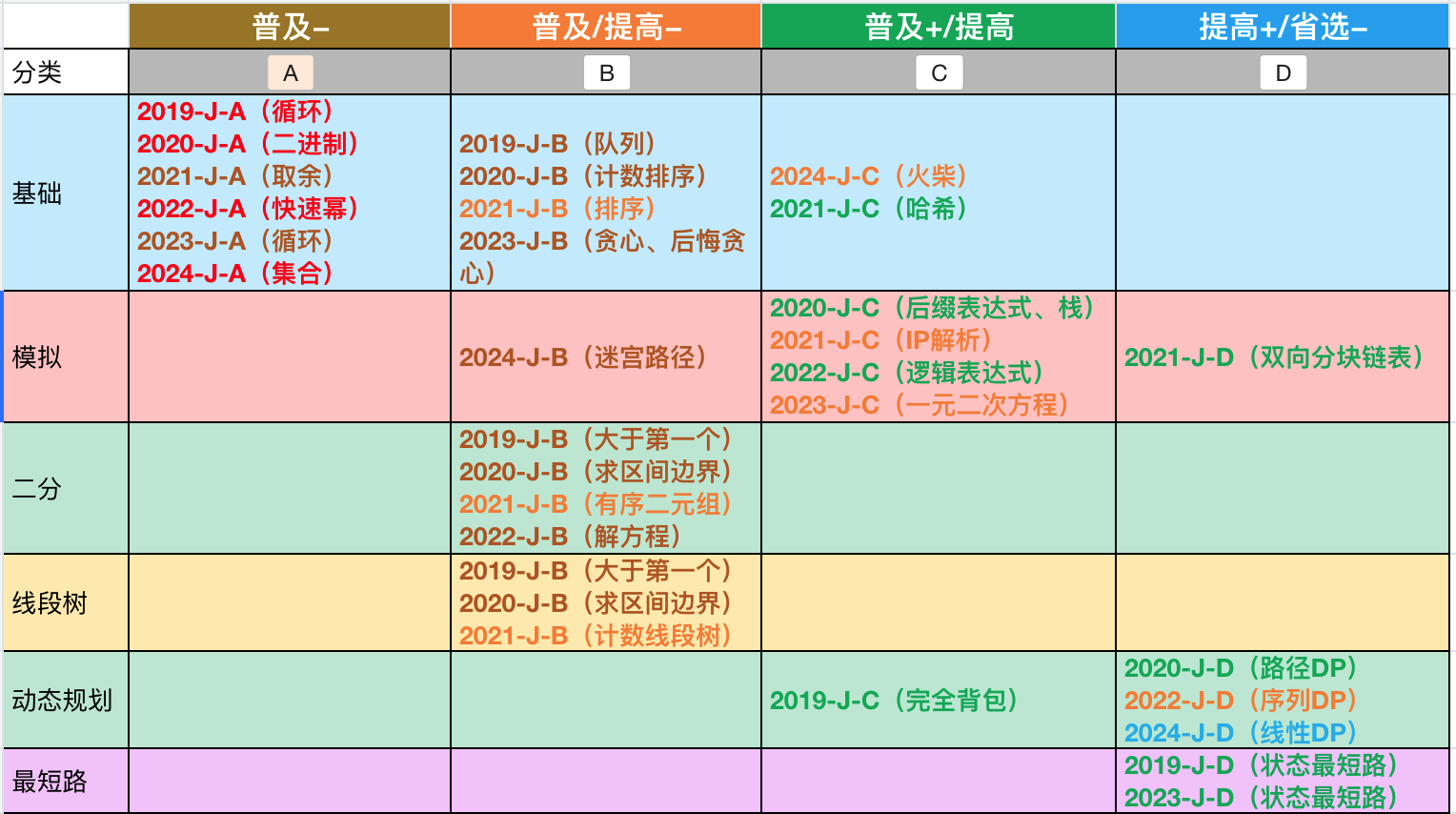
下图是 CSP-S 历年真题的题型分布,其中有 2 道题可以使用线段树,同样其中一道可以使用基础算法优先队列代替线段树。
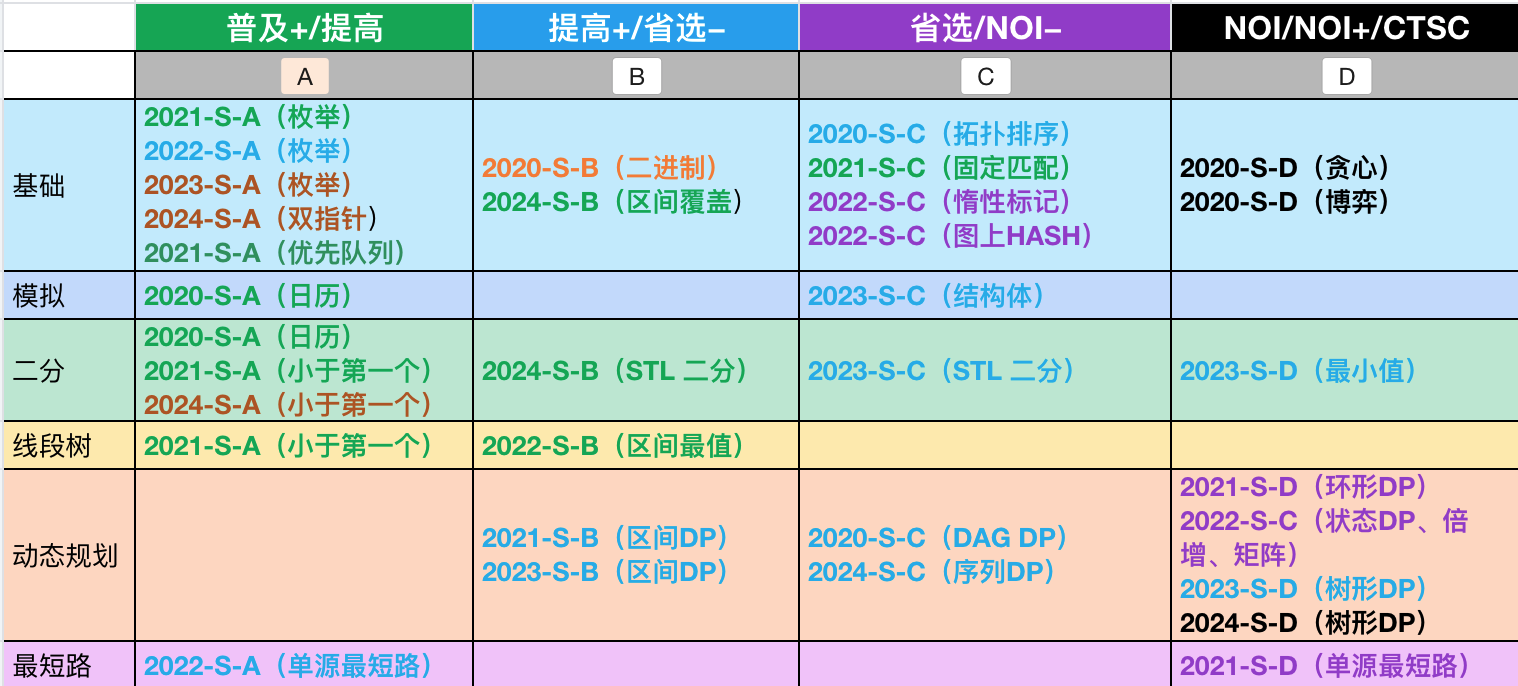
合起来供 5 道题可以使用线段树。
其中 4 道都是单点更新,也可以不使用线段树(需要能想到相关解法)。
最后 1 道必须使用线段树,且不是普通的区间最值,属于线段树高级查询方法,求值时做特殊处理。
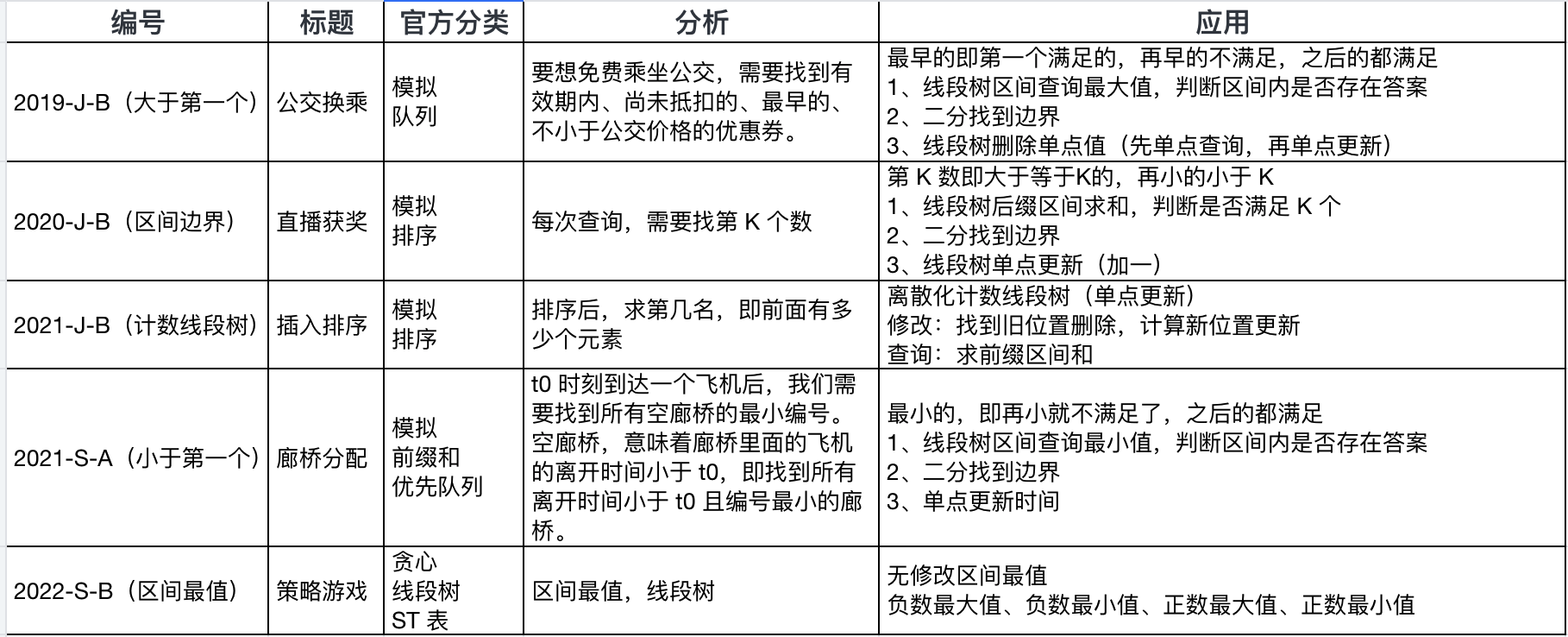
这里重点来看下最后一道题。
2022-S-B 策略游戏。
想到贪心策略后,可以发现需要求出指定区间的正数最值、是否有0值、负数最值。
如果一个区间都是正数,显然没有负数最小值和负数最大值,也没有0值。
即存在某个最值不存在的情况。
正常情况下,叶子节点的最值就是其自身的值。
在这里,需要把最值初始化为无穷值,来代表不存在。
例如负数最大值和正数最大值,初始化为负无穷;
负数最小值和正数最小值,初始化为正无穷。
由于需要 5 个查询结果,这里封装为一个结构体,方便一次查询全部返回。
const ll kMaxVal = 10e9 + 10;
const ll kMinVal = -kMaxVal;
struct Node {
ll negMin = kMaxVal, negMax = kMinVal, posMin = kMaxVal, posMax = kMinVal, zero = 0;
};
初始化时,根据元素值的符号,初始化对应的最值。
具体来说,就是只有元素值时正数时,才能更新正数最值;负数和0值也是一样的逻辑。
void Build(int l = 1, int r = maxNM, int rt = 1) {
if (l == r) {
const ll& val = str[l];
if (val > 0) {
nodes[rt].posMin = min(nodes[rt].posMin, val);
nodes[rt].posMax = max(nodes[rt].posMax, val);
} else if (val < 0) {
nodes[rt].negMin = min(nodes[rt].negMin, val);
nodes[rt].negMax = max(nodes[rt].negMax, val);
} else {
nodes[rt].zero = 1;
}
return;
}
int m = (l + r) >> 1;
Build(lson);
Build(rson);
PushUp(rt, l, r);
}
合并节点时,四个最值可以直接合并,0 值可以通过加法或按位或运算合并。
Node merge(const Node& left, const Node& right) {
Node cur;
cur.negMin = min(left.negMin, right.negMin);
cur.negMax = max(left.negMax, right.negMax);
cur.posMin = min(left.posMin, right.posMin);
cur.posMax = max(left.posMax, right.posMax);
cur.zero = left.zero + right.zero;
return cur;
}
// 合并函数,按需进行合并
void PushUp(int rt, int l, int r) { //
nodes[rt] = merge(nodes[rt << 1], nodes[rt << 1 | 1]);
}
由于这道题不存在更新,不需要延迟标记,查询直接合并左右子树即可。
Node Query(int L, int R, int l = 1, int r = maxNM, int rt = 1) {
if (L <= l && r <= R) {
return nodes[rt];
}
int m = (l + r) >> 1;
Node node;
if (L <= m) {
node = merge(node, Query(L, R, lson));
}
if (m < R) {
node = merge(node, Query(L, R, rson));
}
return node;
}
三、总结
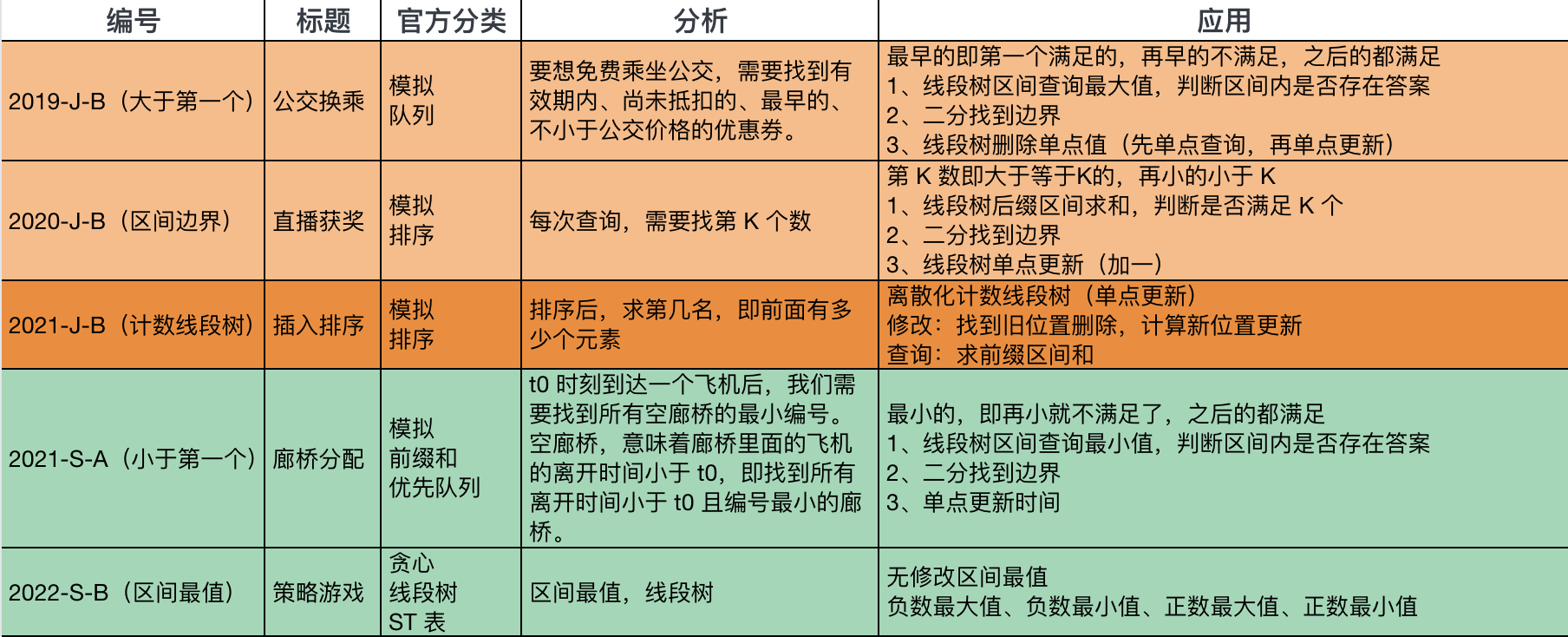
回顾历年 CSP 真题,其实严格来说,只有一道 CSP-S 的题是必须用线段树或者倍增的。
其他题呢?不用也能做,用一些贪心、构造或者巧一点的数据结构都能过。
不过我自己有点不一样的看法。
确实,大纲里写得很清楚:CSP-J 不要求掌握线段树;CSP-S 的题也不一定非得用。
有时候数据还比较弱,用点小技巧也能过。
但问题是——
如果一道题你用线段树能又快又稳拿满分,
而不用线段树就得绞尽脑汁想启发式算法、还得花时间验证对不对,
那到底哪个更划算?
更现实一点,很多同学其实是同时参加 CSP-J 和 CSP-S 的。
也就是说,就算 J 段不要求,大家也已经学习了 S 段的线段树。
比赛的目标是拿高分嘛,不是只待在大纲框框里。
大纲只是保证题目可以用这些知识点解决,是给出题人参考的
但不代表你只能用这些知识点。
举个例子:
一道题你不用线段树,可能只能拿 20 分;
或者花两小时只能拿 50 分;
可你要是会线段树,半小时直接满分。
那你会怎么选?
《完》
-EOF-
本文公众号:天空的代码世界
个人微信号:tiankonguse
公众号 ID:tiankonguse-code
本文首发于公众号:天空的代码世界,微信号:tiankonguse
如果你想留言,可以在微信里面关注公众号进行留言。
