近 6 年 CSP-J/S 题型总结之动态规划

零、背景

CSP-J/S 是从 2019 年开始举办的。

之前已经在《近 6 年 CSP-J 算法题型分析》和《历年 CSP-S 算法题型分析》两篇文章里总结了 CSP-J 和 CSP-S 的题型。

接下来我的规划分两部分：

第一部分：介绍常见算法如何实现，以及在历年真题中是如何应用的。
第二部分：介绍面对比赛时，使用什么样的策略，才能尽可能拿到更高的分数。

第一部分已经分享了二分、线段树、状态最短路。
第二部分已经分享了得分技巧、环境准备。

这篇文章属于第一部分第四篇，打算介绍一下出现频率最高的动态规划。

一、算法介绍

CSP-J（入门级）对动态规划的要求相对宽松，主要考察基础动态规划概念和简单应用，例如一维序列DP、简单背包（0/1背包、完全背包）、简单区间动态规划。
CSP-S（提高级）则建议熟练实现更复杂的DP模型和优化技巧，例如树型DP、状态压缩DP、动态规划的常用优化（如单调队列优化、斜率优化、四边形不等式优化）。

动态规划是信息学竞赛中一个极其重要且常见的核心思想。

其核心思想是将一个复杂的问题分解成若干个相互联系的、更简单的子问题，并通过解决这些子问题来最终解决原问题。
与分治法不同，动态规划的子问题通常是重叠的，因此可以通过记忆化（存储子问题的解）来避免重复计算，极大地提高效率。

动态规划有三大要素：最优子结构、重叠子问题、无后效性。

最优子结构

含义：一个问题的最优解包含其子问题的最优解。
简单来说：要解决大问题，必须先最优地解决其小规模的子问题。
例子：在找最短路径问题中，如果从A到C的最短路径经过B，那么这条路径上从A到B的部分，也必须是A到B的最短路径。

重叠子问题

含义：在递归地求解问题时，会反复遇到相同的子问题。
简单来说：问题的分解方式会导致很多重复的计算。
经典例子：计算斐波那契数列 F(5) = F(4) + F(3)，而 F(4) = F(3) + F(2)。
这里 F(3) 就被计算了两次。如果不做记忆化，重复计算会呈指数级增长。

无后效性

含义：一旦一个子问题的解被确定，后续的决策不会影响它。即“未来与过去无关”。
简单来说：在求解过程的任意阶段，当前的状态就是一个完整的总结，如何到达这个状态的历史信息不会影响未来的演变。
例子：在迷宫问题中，我们只关心当前所在的坐标，而不关心是经过哪条路径到达这里的。当前的坐标（状态）足以决定后续能走向哪里。
这也是我们在定义状态时，经常遇到这样的定义：前 i 个元素中选择第 i 个元素的最优解，后续决策只与这 i 个元素有关，而与之前的元素无关。

二、常见题型

动态规划的题型非常多样，以下是一些常见的题型分类：

• 线性DP
• 背包DP
• 倍增DP
• 区间DP
• 树形DP
• 环形DP
• 计数DP
• 状压DP
• 数位DP
• 概率DP

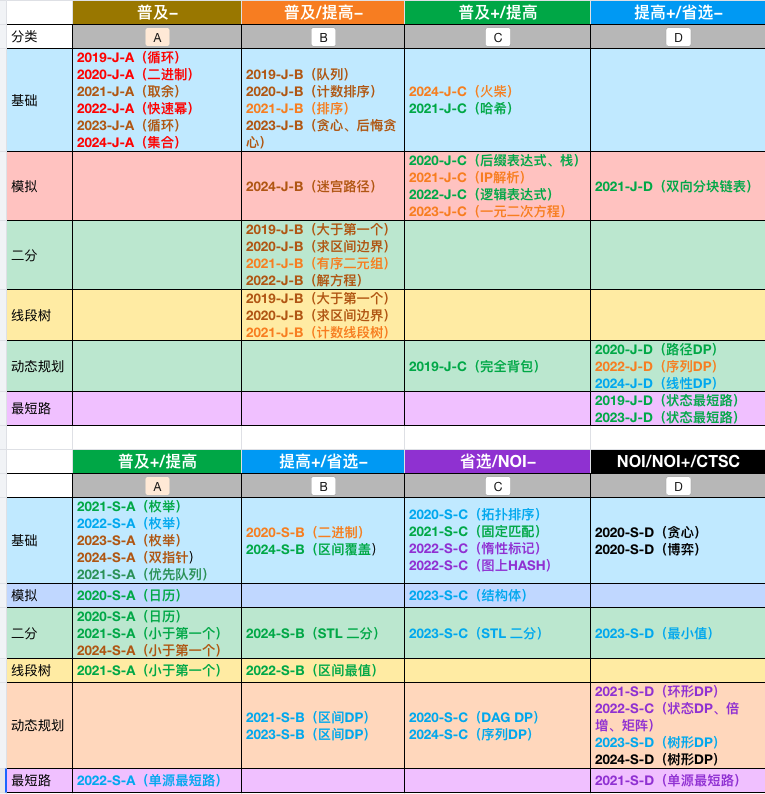
分析近 6 年的 CSP-J/S 题目，有 11 道题涉及动态规划，涉及上面 7 个分类。

三、背包DP

2019 年 J 级 C 题《纪念品》，就是一个最简单的完全背包模板题。

背包问题出现概率最高的是 0/1 背包和完全背包。

0/1 背包：每个物品只能选一次。
当把二维数组压缩为一维数组时，为了避免被自身影响，通常从后向前遍历。

for (int i = W; i >= w; --i) {
    dp[i] = max(dp[i], dp[i - w] + v);
}

完全背包：每个物品可以选无数次。
从前到后遍历会允许当前物品被重复使用，从而实现“可选无数次”，因此完全背包应当从前向后遍历。

for (int i = w; i <= W; ++i) {
    dp[i] = max(dp[i], dp[i - w] + v);
}

要点小结：

• 常见变体：0/1 背包、完全背包、多重背包（每件有限次，可用二进制拆分转 0/1）、混合背包（多种类型并存）。
• 复杂度：若容量为 W、物品数 n，经典转移为 O(nW)。
• 易错点：一维滚动时的遍历方向；初始化（如 dp[0]=0，其它为 -inf/0 取决于“可行/最大值”的语义）；答案位置（是 dp[W] 还是 max dp[<=W]）。
• 常用优化：分组背包的单调队列优化；Bitset 优化（大 W、小权值计数时）；按价值做容量转换（小价值时）。

四、线性DP

线性 DP 是动态规划中最常见的类型，通常用于处理序列问题(一维或者二维)。
这里我把序列 DP 和 网格 DP 都归为线性 DP。

这类 DP 的状态通常是一个一维数组或者二维数组，表示前 i 个元素某种状态的最优解。

例如各年真题的状态如下：

2020-J-D 题的《方格取数》，定义每一列的每一行的状态为 dp[i][j]，表示到达第 i 行第 j 列的最优解。
2022-J-D 题的《上升点列》，定义每个点的状态为 dp[i][j]，表示第 i 个为结尾使用 j 个的最优值。
2024-J-D 题的《接龙》，定义状态为 dp[i][j]，表示第 i 轮接龙时，以第 j 个数为结尾的最优值。
2024-S-C 题的《染色》，定义状态为 dp[i][j]，表示第 i 个元素归属第 j 个子序列时的最优值。

可以发现，都是定义前缀某种状态的最优解。
然后前缀的长度不断增加，计算出下个位置前缀的最优解。
从而不断循环下去，计算出整个序列的最优解。

要点小结：

• 转移方向：按依赖关系决定（如从左到右、从上到下、按层/对角线）。
• 常见优化：前缀最值/差分、单调队列（滑动窗口最值 DP）、前缀和/二维前缀和、LIS 的 O(n log n) 解法与 DP 的对比取舍。
• 易错点：初值与无解状态；答案位置（末位/全局最值）；越界与障碍判定；转移覆盖不全导致漏解。

五、区间DP

区间 DP 是动态规划中处理区间问题的常用方法。
它通常用于处理一些需要在区间内进行决策的问题，例如区间合并、区间分割等。

区间 DP 的状态通常是一个二维数组，表示某个区间的最优解。

例如某些“合并/加括号/石子合并”类题，可定义 dp[i][j] 表示区间 [i,j] 的最优值或代价。
这类模型通常有 O(n^2) 个状态；若每个状态通过枚举切分点转移，时间复杂度为 O(n^3)，因此 n 往往在几百量级。

如果每个状态的转移是通过枚举区间内的某个位置来进行决策的，复杂度就会是 O(n^3)。

这个时候就需要看数据范围了，如果数据范围较小，可以直接枚举。
如果数据范围较大，就需要考虑某种优化，来降低复杂度。

要点小结：

• 常见优化：四边形不等式优化、Knuth 优化（满足决策点单调且四边形不等式）；分治优化（凸性/单峰性）。
• 拆环技巧：对环形问题常通过“固定断点/复制数组取长度 n 的区间”来转化（见下节）。
• 易错点：转移方向应按区间长度从小到大；初始化（长度 1/空区间）；决策点边界；是否需要记录决策点以便优化。

六、环形DP

环形DP是处理环形结构问题的动态规划方法，算是区间DP的一种扩展。

在环形DP中，我们通常需要将环形结构“展开”成线性结构，以便使用常规的DP方法进行求解。

具体来说，在枚举子问题时，需要考虑两种情况来处理环形DP问题：

1. 不包含首尾元素的情况：直接在区间DP的基础上进行求解。
2. 包含首尾元素的情况：将首尾元素视为一个整体，重新定义状态进行求解。

例如 2021-S-D 题的《交通规划》，最后一步就需要枚举分割线，将一个环拆分为两个序列。

// 第二步：计算环形DP的最优值
dp.clear();
dp.resize(k, vector<ll>(k, -1));
ll ans = INFL;
for (int a = 0; a < k; a++) {
  for (int b = a + 1; b < k; b += 2) {  // 奇数点只能连偶数点
    ans = min(ans, indexDis[a][b] + Dfs(a, b) + Dfs(b, a));
  }
}

要点小结：

• 常见做法：
  • 枚举断点，将环拆成链；或将数组复制一倍，在长度为 n 的滑动区间内做线性/区间 DP。
  • 对“不能同时取首尾”的题，分两次做“取首不取尾/取尾不取首”。
• 复杂度：较线性多一重“断点/区间”的枚举，常见为 O(n^2) 或在优化后达到 O(n log n)。
• 易错点：重复计数与边界重叠；答案是否需遍历所有断点取最优。

七、计数DP

计数DP是动态规划中用于计算满足特定条件的组合数量的方法。

其实这个题型与 线性 DP 与 区间 DP 类似，只不过状态表示的不是最优值，而是满足某种条件的“方案数”（通常要取模）。

要点小结：

• 取模处理：常见 1e9+7；注意加法取模与负数取模处理。
• 初始化：空方案是否计为 1；边界状态的计数是否为 0/1。
• 组合数预处理：涉及选取/排列时常结合 C(n,k) 或阶乘逆元；也可与容斥/生成函数搭配。
• 易错点：重复计数与顺序相关性（排列 vs 组合）；状态维度不足导致漏计；大数溢出。

八、倍增DP

倍增DP是一种基于二进制思想，通过预处理和存储中间结果的方式，来加速查询的动态规划方法。

具体来说，朴素的区间定义是 (l, r)，而倍增的区间定义是 (i, k)，表示从位置 i 开始，长度为 2^k 的区间。
这样，区间 (i, k+1) 可以通过合并两个长度为 2^k 的区间 (i, k) 和 (i + 2^k, k) 来得到。

当需要求解任意区间 (l, r) 的问题时，可以基于二进制思想，将其拆分为若干个倍增区间的组合，从而快速得到结果。

例如 2022-S-D 题的《数据传输》，就是在树上倍增 DP 的应用。

要点小结：

• 典型应用：二进制跳跃（走 k 步/最远可达）、LCA、RMQ 稀疏表。
• 复杂度：预处理 O(n log n)；查询 O(1)/O(log n) 取决于函数是否可 O(1) 合并。
• 易错点：函数是否满足结合性/幂等性（关系到能否稀疏表 O(1) 合并）；边界（第 0 层）与不可达标记；按位合并的顺序。

九、树形DP

树形DP是一种用于处理树形结构问题的动态规划方法。

在树形DP中，我们通常需要将树的每个节点视为一个状态，并通过动态规划的方式来计算每个状态的最优解。

这里，我把真题 2020-S-C 《函数调用》也归为树形 DP，其实也可以归属为 DAG DP。
DAG 是有向无环图，每个顶点可以通过所有前驱来计算答案，或者通过所有后继来计算答案，与树形 DP 十分类似。

要点小结：

• 常见范式：
  • 子树 DP（自底向上）：汇总子节点信息（如最大独立集、树形背包、直径）。
  • 换根 DP（rerooting）：先做一次子树 DP，再换根传递得到全局每点答案。
• 复杂度：通常 O(n) 或 O(n log n)（视合并/数据结构而定）。
• 易错点：树的输入是否有重边/非连通；根的选择；合并顺序与初值；避免重复计算（如清理全局变量）。

十、状态压缩DP

状态压缩DP是一种通过使用位运算来表示状态，从而减少状态空间的动态规划方法。

这类题目元素个数通常不会太多，一般在 20 个以内。
但是状态涉及到元素集合，此时就可以使用位运算来表示集合，从而大幅减少状态空间。

状压有两种常见的枚举方式：

一种是枚举所有子集，这时候需要通过 (sub - 1) & mask 来快速得到下个不重复的子集。

for (int sub = mask; sub; sub = (sub - 1) & mask) {
    // 处理子集 sub  
}

另一种是枚举值为 1 或 0 的位置，这时候一般直接循环判断。

int dfs(const int pre, const int mask) {
  int& ret = dp[pre][mask];
  if (ret != -1) return ret;
  for (int i = 0; i < n; ++i) { // 枚举每一位
    if(!(mask & (1 << i))) continue; // 前面已选择
    int nextPre = CalcNextPre(pre, i);
    int nextMask = mask ^ (1 << i);
    if (dfs(nextPre, nextMask)) {
      path[pre][mask] = i; // 记录最优路径
      return ret = 1;
    }
  }
  return ret = 0;
}

要点小结：

• 典型模型：TSP/Hamilton 路，dp[mask][i] 表示走过集合 mask、当前在 i 的最优值/可达性；状压匹配；覆盖类问题。
• 复杂度：O(n·2^n) 或 O(n^2·2^n) 级别；内存注意 2^n 乘以附加维度。
• 枚举技巧：遍历子集 (sub-1)&mask；
• 易错点：初值与不可达态；记忆化表维度与默认值；位运算优先级与括号。

十一、数位DP

数位 DP 是一种用于处理大整数问题的动态规划方法。
最常见的是不大于某个数字、且满足某种性质的数字个数。

通过数位 DP，通常将问题划分为“当前前缀等于上界前缀”和“当前前缀小于上界前缀”两类情况。

当当前前缀小于上界前缀时，后续位可自由选择，通常能直接累加方案；
当当前前缀等于上界前缀时，继续在下一位划分为“等于/小于上界”的两种情况递归下去。由此可用记忆化搜索或自底向上的 DP 得到最终答案。

当然，有时候数位 DP 也会有上下界，这个时候更复杂一些。

要点小结：

• 常见状态：位置 pos、是否受限 tight、是否前导零 lead、附加统计量（如数位和/余数/上一个数位）。
• 复杂度：约为“位数 × 每位可选种类 × 附加状态规模”。
• 易错点：前导零是否参与性质统计；上下界双界的处理（用 solve(R)-solve(L-1)）；含等号边界的 off-by-one。

十二、概率DP

概率DP是一种用于处理涉及概率计算问题的动态规划方法。
这种题目一般比较复杂，几乎不会出现在 CSP-J/S 中。

十三、最后

可以看到，动态规划的题型非常多样，涵盖了从基础的一维DP到复杂的状态压缩DP等多种类型。

在实际应用中，我们需要根据具体问题的特点，选择合适的DP方法来进行求解。

想要深入理解动态规划，建议多练习不同类型的DP题目，并尝试总结其共性和差异。

补充一个比赛中可用的通用清单：

建模六步：

1) 定义状态（必要最小充分信息）
2) 明确初值（可行/不可行的默认值）
3) 写出转移（保证覆盖且不重不漏）
4) 确定顺序（拓扑、长度、方向）
5) 选定答案位置（末态/集合最值/计数和）
6) 估算复杂度与是否需优化（单调队列/Knuth/四边形不等式/倍增/状压等）

Debug 小贴士：先写小数据暴力比对；打印关键中间态；为不可达态设明显哨值；逐步放开优化。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code