历年 CSP-J/S 题型总结之状态最短路

作者: tiankonguse | 更新日期:

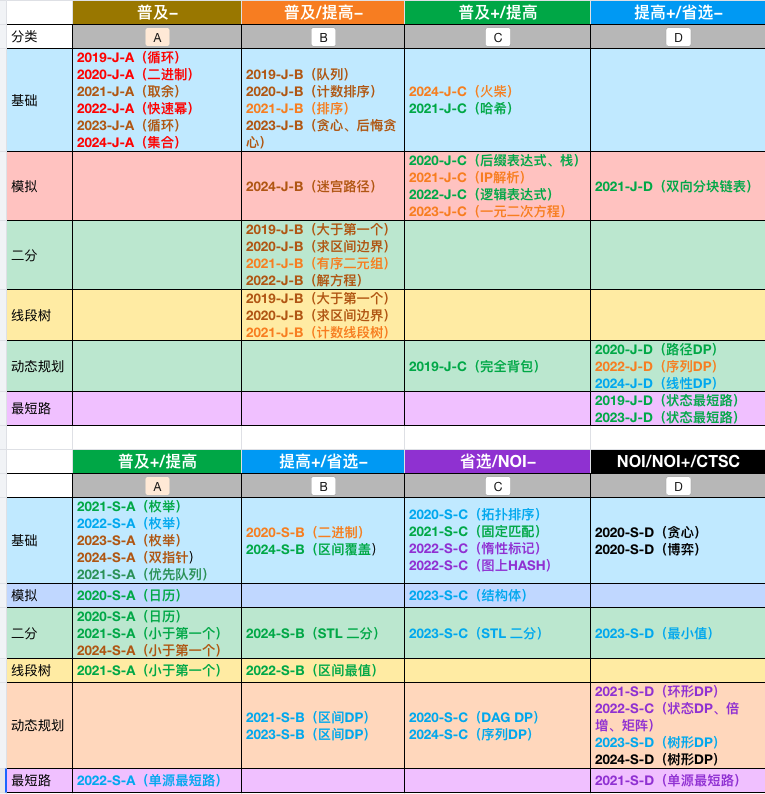
二分、线段树、动态规划、最短路

本文首发于公众号：天空的代码世界，微信号：tiankonguse

零、背景

CSP-J/S 是从 2019 年开始举办的。

之前已经在《近 6 年 CSP-J 算法题型分析》和《历年 CSP-S 算法题型分析》两篇文章里总结了 CSP-J 和 CSP-S 的题型。

接下来我的规划分两部分：

第一部分：介绍常见算法如何实现，以及在历年真题中是如何应用的。
第二部分：介绍面对比赛时，使用什么样的策略，才能尽可能拿到更高的分数。

第一部分的第一篇文章是二分，之前已经在《CSP-J/S 题型总结之二分》分享过了。
第一部分的第二篇文章是线段树，之前已经在《CSP-J/S 题型总结之线段树》分享过了。
第二部分的第一篇文章是得分技巧，之前已经在《CSP-J/S 备赛：5 个实用方法拿更多的分》分享过了。
第二部分的第二篇文章是环境准备，之前已经在《CSP-J/S 备赛必学之环境准备》分享过了。

这篇文章属于第一部分第三篇，打算介绍一下出现频率很高的状态最短路。

状态最短路示意图

一、算法介绍

CSP-J（入门级）对最短路算法的要求相对宽松，掌握图的基本概念（如节点、边、权重）、图的存储方式（邻接矩阵、邻接表）、以及无权图的最短路（广度优先搜索，BFS）通常就能覆盖大部分考点。
CSP-S（提高级）则建议熟练实现 Dijkstra（推荐堆优化版）、SPFA、Floyd，并理解负权图的处理要点；“次短路”了解概念即可。

如今 STL 已是基础库，不需要自己手写堆了。
所以强烈建议熟练掌握 Dijkstra 的堆优化写法。
因为“状态最短路”通常就是在 Dijkstra 基础上叠一维（或多维）状态，并用堆优化来实现。

二、图的存储

实际比赛中，我们几乎所有的图都是使用邻接表来存储的。

如果是无权图，邻接的就是顶点列表。

vector<vector<int>> g(n); 
while (m--) {
  int u, v;
  scanf("%d%d", &u, &v);
  g[u].push_back(v);
  g[v].push_back(u);
}

如果是有权图，则邻接的是二元组。

using ll = long long;
vector<vector<pair<ll, int>>> g(n);
while (m--) {
  int u, v;
  ll w;
  scanf("%d%d%lld", &u, &v, &w);
  g[u].push_back({w, v});
  g[v].push_back({w, u});
}

三、朴素最短路

如果是无边权的最短路，直接使用队列 BFS 即可。

// 求 0 的单源最短路
vector<int> dis(n, -1);
queue<pair<int, int>> que;
auto Add = [&](int v, int step) {
  if (dis[v] != -1) return;
  dis[v] = step;
  que.push({v, step});
};
Add(0, 0);
while (!que.empty()) {
  const auto [u, step] = que.front();
  que.pop();
  const int nextStep = step + 1;
  for (auto v : g[u]) {
    Add(v, nextStep);
  }
}

如果是带边权的最短路，就用优先队列堆优化的 Dijkstra。

using ll = long long;
template <class T>
using min_queue = priority_queue<T, vector<T>, greater<T>>;

// 求 0 的单源最短路
const ll INF = (1LL << 62);
vector<ll> dis(n, INF);
min_queue<pair<ll, int>> que;
auto Add = [&](int v, ll step) {
  if (dis[v] <= step) return;
  dis[v] = step;
  que.push({step, v});
};
Add(0, 0);
while (!que.empty()) {
  const auto [uw, u] = que.top();
  que.pop();
  if (uw != dis[u]) continue; // 跳过过期状态
  for (auto [vw, v] : g[u]) {
    Add(v, uw + vw);
  }
}

四、状态最短路

状态最短路的思路与动态规划相似：把“节点 × 状态”视作扩展图上的新节点，在这张“扩展图”上跑最短路。

朴素的最短路只需要一个一维数组 dis[v] 表示从源点到 v 的最短距离。
状态最短路则是二维甚至多维数组，例如 dis[state][v] 表示“当 v 处于某个状态 state 时”的最短距离。

例如 2019 J 组 D 题《加工零件》，状态是按步数奇偶划分；
2023 J 组 D 题《旅游巴士》，状态是按模 k 划分。
这两道题的状态都是最短路取模上一个值代表状态，比较容易理解，大家可以用来参考学习。

“加工零件”没有边权，所以直接用队列 BFS 即可。

// 求 0 的单源最短路
vector<vector<int>> dis(2, vector<int>(n, -1)); // 2 个状态：偶/奇
queue<pair<int, int>> que; // {state, node}
auto Add = [&](int v, int state, int step) {
  if (dis[state][v] != -1) return;
  dis[state][v] = step;
  que.push({state, v});
};
Add(0, 0, 0);
while (!que.empty()) {
  const auto [state, u] = que.front();
  que.pop();
  const int nextStep = dis[state][u] + 1;
  const int nextState = (state + 1) % 2; // 每走一条边，奇偶翻转
  for (auto v : g[u]) {
    Add(v, nextState, nextStep);
  }
}

“旅游巴士”是带权图上的状态最短路。

// K 状态的 Dijkstra（以“距离模 K”为例，按题意也可改为“步数模 K”）
using ll = long long;
template <class T>
using min_queue = priority_queue<T, vector<T>, greater<T>>;

const int K = /* 例如 2，或题目给定的 k */ 2;
const ll INF = (1LL << 62);

// dis[s][v]：到达节点 v 且状态为 s 的最短距离
vector<vector<ll>> dis(K, vector<ll>(n, INF));

// 最小堆里放三元组 {距离d, 状态s, 节点u}
using Node = tuple<ll, int, int>;
min_queue<Node> pq;

auto push = [&](int s, int v, ll d) {
  if (d < dis[s][v]) {
    dis[s][v] = d;
    pq.emplace(d, s, v);
  }
};

push(0, 0, 0); // 从源点 0，初始状态 0 出发
while (!pq.empty()) {
  auto [d, s, u] = pq.top();
  pq.pop();
  if (d != dis[s][u]) continue; // 过期
  for (auto [w, v] : g[u]) {
    ll nd = d + w;
    // 若状态按“距离/时间”取模：
    int ns = (int)(nd % K);
    // 若状态按“步数（边数）”取模，请改为：int ns = (s + 1) % K;
    push(ns, v, nd);
  }
}

常见易错点：

  • 距离与 INF 建议用 long long；不要填进 int导致整数越界。
  • 堆弹出时要判“过期”（if (d != dis[...]) continue;），否则会多做无效松弛。
  • 状态转移要与题意一致：是按“步数”还是按“累计时间/距离”取模，或按边属性切换。
  • 起点可能需要初始化多个状态（看题意，比如初始状态不唯一）。
  • 终点答案可能是 min_s dis[s][t]，别忘了在所有状态里取最小值。

五、最后

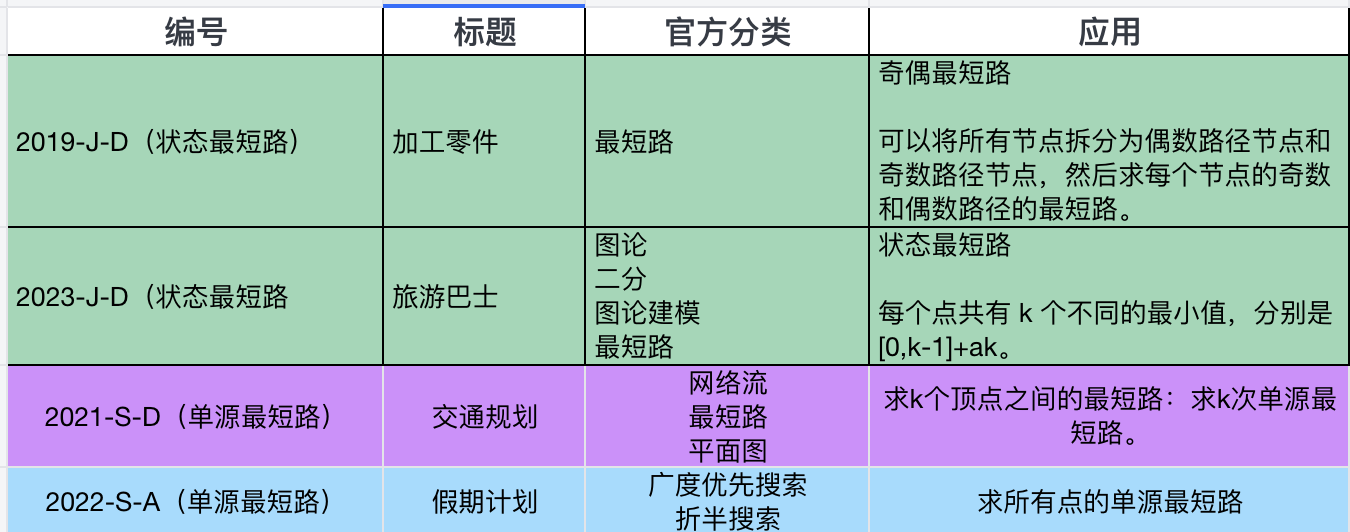
状态最短路示意图

2019-J-D（状态最短路）和 2023-J-D（状态最短路） 一个状态为 2，一个状态为 K，本质上没有区别。

2021-S-D（单源最短路）和 2022-S-A（单源最短路） 就是朴素的最短路。

总的来说，CSP-J 也出现了两次“状态最短路”，CSP-S 更常把最短路作为综合题的一环；关键在于：

  • 熟练 Dijkstra 的堆优化与“跳过过期”写法；
  • 能根据题意正确“建图/建状态”，把问题转化为“扩展图上的最短路”。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。

关注公众号,接收最新消息

置顶文章

tiankonguse + ≡
穿越