CSP-S 2025 第三题 字典树 Trie 解法

零、背景

目前我已经做了历年 CSP-J/S 的所有常规算法题目。
CSP-J 题解：2025、2024、2023、2022、2021、2020、2019。
CSP-S 题解：2025、2024、2023、2022、2021、2020。

后来对历年题型做了总结，《CSP-J 题型分析》和《CSP-S 题型分析》。

最后也分享了备考策略与常见算法，如
备考策略：得分技巧、环境准备。
常见算法：二分、线段树、状态最短路、动态规划、数学、常见算法和数据结构。

在之前的《CSP-S 2025 第二轮比赛题解》文章中，第三题“谐音替换”（replace）我介绍了 AC 自动机 + 哈希的解法。

当时提到最优解是 AC 自动机 + 哈希。
据说也可以 Trie + 哈希，后面我研究下再分享。

这几天一直在思考如何介绍字典树 Trie 的解法，发现涉及到大量相对少见的知识点。
所以，思考了三天。最终决定先简要铺垫这些前置知识，再介绍 Trie 解法。

PS：有人找我要源码，我放在网盘里了，有需要的可以关注公众号，回复 CSP-S-2025-C-TRIE 获取。

一、题目回顾

题目：给 n 个字符串二元组 (s1, s2)，以及 q 个询问二元组 (t1, t2)。
问对于每个 (t1, t2)，有多少个 (s1, s2) 满足在 s1 中的子串 t1 替换为 t2 后可以得到字符串 s2 。

经过一番分析，可以发现这些字符串需要按键进行分组处理。
s1 可以分为三部分：公共前缀 A、替换部分 B、公共后缀 C。
s2 也可以分为三部分：公共前缀 A、替换部分 D、公共后缀 C。 (t1, t2) 也是类似的，t1 分为 AA、B、CC，t2 分为 AA、D、CC。

要想满足替换条件，第一个条件是必须满足 (s1, s2) 的 B->D 和 (t1, t2) 的 B->D 是相同的。
所以，可以根据 B->D 来对数据进行分组。

分组后， (s1, s2) 转化为了 (A, C)。
(t1, t2) 也转化为了 (AA, CC)。

此时，要满足替换条件，A 必须是 AA 的后缀，C 必须是 CC 的前缀。

所以，问题转化为了： 对于每个询问 (AA, CC)，统计有多少个 (A, C) 满足 A 是 AA 的后缀，C 是 CC 的前缀。

二、AC 自动机解法回顾

在之前的文章中，我介绍了 AC 自动机的解法。

简单来说，把 (A, C) 拼接为 A#C，把 (AA, CC) 拼接为 AA#CC。
问题就转化为了 ： 统计有多少个 A#C 是 AA#CC 的子串。

这个直接用 AC 自动机就可以解决。
伪代码如下：

for (int i = 0; i < n; i++) { // h 为分组的唯一表示
  AC::insert(ACIndex[h], pattern.c_str());
}

for (auto& [_, root] : ACIndex) {
  AC::build(root); // 每个分组单独构建 AC 自动机
}

while (q--) { // q 个询问
  // text 为查询串，例如 text = TA + "#" + TC
  ll res = AC::query(root, text.c_str());
  printf("%lld\n", res);
}

分析 AC 自动机的匹配过程，虽然 fail 指针加速了匹配过程。
但是在最坏情况下，如果全部都匹配，复杂度仍然是 O(q*m)。

因此 AC 自动机并不是最优解；在更严苛的数据下可能会 TLE。

三、前置知识：区间覆盖点

为了引出差分线段树的知识点，这里分三个阶段来看区间覆盖点问题。

阶段1：单点查询

题目： 给定 n 个区间 [l, r]，问某个点 x 被多少个区间覆盖。

暴力：扫描所有区间进行判断，复杂度 O(n)。
线段树：区间更新，复杂度 O(n log n)；再单点查询，复杂度 O(log n)。
差分数组：先对区间进行差分，复杂度 O(n)；离线求前缀和，复杂度 O(n)；再单点查询，复杂度 O(1)。

总结：没有更新，只询问单点，暴力和差分数组是最优解。

阶段2：多次静态查询

题目： 给定 n 个区间 [l, r]，问 q 个点 x1, x2, ..., xq 分别被多少个区间覆盖。

暴力：扫描所有区间进行判断，复杂度 O(n*q)。
线段树：区间更新，复杂度 O(n log n)；再 q 次单点查询，复杂度 O(q log n)。
离线差分：先对区间进行差分，复杂度 O(n)；离线求前缀和，复杂度 O(n)；再 q 次单点查询，复杂度 O(q)。

差分的前缀和就是答案，线段树恰好可以快速计算前缀和。
故差分可以和线段树结合，得到差分线段树。
区间插入复杂度 O(n log n)，q 次前缀和查询，复杂度 O(q log n)。

可以发现，差分线段树和线段树的复杂度是一样的。

阶段3：动态更新与查询

题目： 给一个操作序列，可能为插入一个区间或查询某个点 x 被多少个区间覆盖。
其中插入区间操作有 m 次，查询点操作有 q 次。

线段树依旧比较优秀，累计更新复杂度 O(m log n)，累计查询复杂度 O(q log n)。
离线差分：由于差分查询前都需要扫描计算前缀和，累计复杂度退化为 O(m + q*n)。
差分线段树：累计更新复杂度 O(m log n)，累计查询复杂度 O(q log n)。

总结：对于动态更新和查询的区间点覆盖问题，差分线段树和线段树复杂度是一样的，都是最优解。
其中线段树也可以使用树状数组来替代。

四、前置知识：树上路径问题

路径和等于两个父路径和之和。
父路径和等价于两个根路径和之差。
故这里简化问题，只讨论根路径和问题。

同样，分三阶段来看树上路径问题。

阶段1：单次静态查询

题目： 给定一棵树，对其中 n 个节点设置权值。
最后问某个节点 u 到根节点的路径和是多少。

由于要更新树节点，这里假设已经对树节点进行随机编号，可以 O(1) 访问树的任何一个节点。

暴力：更新 n 次节点权值，复杂度 O(n)；查询路径和，复杂度 O(h)，h 为树高。
前缀和：离线预处理路径和，复杂度 O(n)；查询路径和，复杂度 O(1)。

这里要介绍一个新的知识：树的 DFS 序。
对树进行 DFS 遍历，记录每个节点的进入时间 L[u]（入时刻）和离开时的进入时间 R[u]（出时刻），二者随遍历单调递增。
则节点 u 的子树对应的连续区间为 [L[u], R[u]]，即在 DFS 序时间线上，u 的整棵子树被“包裹”在这个区间内。

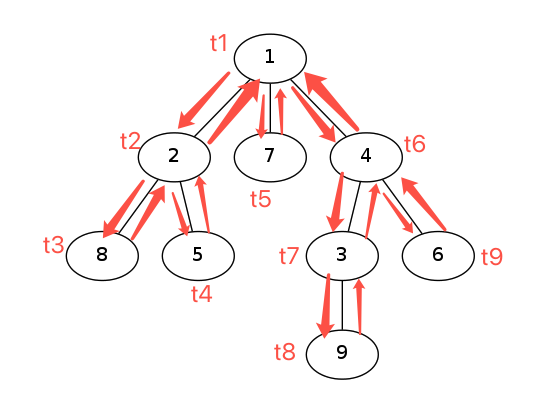
如上图，假设树是从左到右递归遍历的，dfs 序就是：

t:    1 2 3 3 4 4 4 5 5 6 7 8 8 9 9 9 9
in:   1 2 3 3 4 4 2 5 5 6 7 8 8 9 9 6 1
val:  1 2 8 8 5 5 2 7 7 4 3 9 9 6 6 4 1

只看时间序列，对于时间 ti，第一次出现时，代表进入时间 L；第二次出现时，代表离开时间 R。

这个序列有几个很有趣的性质：

性质1：在每个节点的进出时间 [L,R] 之间，是所有子树的进出区间。
性质2：对于一个节点的进入时间 L，序列之前，到根的路径只有进入时间，没有离开时间。
性质3：对于一个节点的进入时间 L，序列之前，根路径之外的节点，进入时间和离开时间是成对出现的。

递归到一个节点时，根据性质2 和性质 3，利用差分进入加权，离开减权。
无关的子树都恰好抵消了，只剩下根路径的节点。

故，树遍历 DFS 序后，可以把树上路径问题转化为区间覆盖点问题。
插入一个节点，就是在进入时间加权，离开时间减权。
查询一个节点，就是查询进入时间的前缀和。

累计插入复杂度 O(n log n)，查询复杂度 O(q log n)。

阶段3：动态更新与查询

静态多次查询比较简单，这里就不再赘述了。
直接来看动态更新和查询。

暴力：O(n) 单点更新，O(q*h) 单点查询。
前缀和：每次查询前都需要重新计算前缀和，复杂度退化为 O(n + q*n)。
差分线段树：与单次静态查询没区别，累计插入复杂度 O(nlog n)，查询复杂度 O(q log n)。

总结：对于动态更新和查询的树上路径问题，通过树的 DFS 序转化为区间覆盖点问题，差分线段树是最优解。

五、前置知识：扫描线

扫描线是一种将二维问题转化为一维问题的技巧。

例如常见的问题有多个矩阵的面积并、多个矩阵面积的周长等。
区间问题也有一些二维查询问题，例如给一些序列，问区间[L,R]内有多少个数在某个范围[X,Y]内。

如下图，以矩阵面积并为例，介绍扫描线的思路。

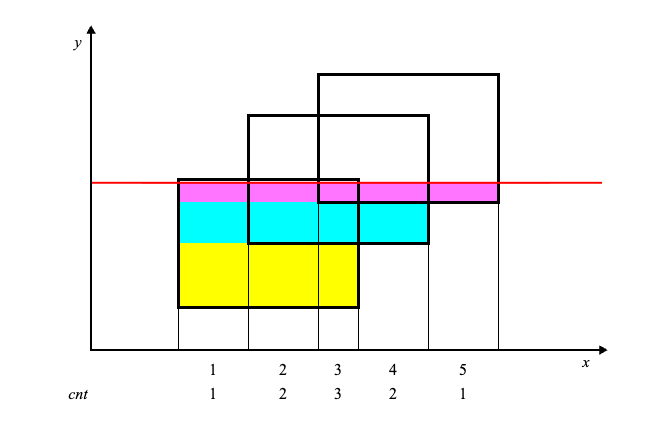
一个维度从小到大枚举扫描，然后将另一个维度转化为区间覆盖点问题。

具体来说，假设从下到上扫描 y 轴。
当扫描到一个矩阵的下边界时，在 x 轴上插入该矩阵的覆盖区间。
当扫描到一个矩阵的上边界时，在 x 轴上删除该矩阵的覆盖区间。
在两个边界之间的扫描过程中，x 轴上被覆盖的长度即为当前扫描线的覆盖长度。
累加每个扫描线段的覆盖长度乘以扫描线段的高度，即为矩阵面积并。

扫描线不限于矩阵面积并问题，其他二维问题也可以使用扫描线转化为一维区间覆盖点问题。
例如下一小节的另一个知识点，就可以把树上二元组问题转化为“树上的扫描线”问题。

六、前置知识：树递归栈的含义

假设我们对一棵树进行深度优先遍历。
进入一个节点时，把这个节点加入一个数据结构。
离开一个节点时，把这个节点从数据结构中删除。

那遍历到某个节点时，数据结构中存储的节点有哪些含义呢？
答案是：数据结构中存储的节点，恰好是从根节点到当前节点的路径上的所有节点。

所以，深度优先搜索的递归栈，恰好存储了从根节点到当前节点的路径。
可以把这条“随 DFS 前进的路径”类比为一条在树上的扫描线。

七、Trie 解法详解

前面介绍了四个前置知识：区间覆盖点、树上路径、扫描线、树递归栈。
现在结合这些知识，来看 Trie 解法。

首先，回顾题目：对于每个询问 (AA, CC)，统计有多少个 (A, C) 满足 A 是 AA 的后缀，C 是 CC 的前缀。

我们可以把左边翻转后的 A 和 AA 构建一棵字典树 Trie1，把右边的 C 和 CC 构建一棵字典树 Trie2。

问题就转化为：统计有多少个 (A, C) 满足 A 在 Trie1 上位于 AA 的根路径上，且 C 在 Trie2 上位于 CC 的根路径上。

结合树扫描线的知识，我们可以对 Trie1 进行深度优先遍历，把遍历到的节点 A 对应的若干 C 加入到另一棵树。
当 Trie1 遍历到 AA 时，递归栈中恰好保留了从根到 AA 的整条路径，因而对应的所有 C 都已加入到树中。
此时我们需要统计这些 C 中，有多少个落在 Trie2 上 CC 的根路径上。

这不就是树上路径问题吗？
我们提前对 Trie2 进行 DFS 序遍历，得到 Trie2 中每个节点的进入时间 L 和离开时间 R。

int in[max6], out[max6];
void Dfs2(int u, int& dfs_index) {
  if (u == -1) return;
  in[u] = ++dfs_index;
  for (int i = 0; i < 26; i++) {
    if (TRIE::nodes[u].next[i] != -1) {
      Dfs2(TRIE::nodes[u].next[i], dfs_index);
    }
  }
  out[u] = dfs_index;
}

之后，在 Trie1 遍历过程中，把对应的 C 以区间差分的形式插入到树状数组/线段树中；
遇到查询时，在 CC 的进入时间 L 处查询前缀和即可得到答案。

void Dfs1(int u) {
  if (u == -1) return;
  updateC(u, 1);
  QueryCC(u);
  for (int i = 0; i < 26; i++) {
    if (TRIE::nodes[u].next[i] != -1) {
      Dfs1(TRIE::nodes[u].next[i]);
    }
  }
  updateC(u, -1);
}

其中 updateC(u, val) 表示把节点 u 对应的所有 C 以差分的方式加到数据结构中（进入加、离开减）。
另外，由于同一个 A 可能对应多个 C，所以 updateC(u, val) 需要把所有对应的 C 都插入或删除。

void updateC(int u, int val) {
  for (auto v : pattern_ids[u]) {
    const int L2 = in[v], R2 = out[v];
    fenwick.Add(R2 + 1, -val);
    fenwick.Add(L2, val);
  }
}

QueryCC(u) 表示查询节点 u 对应的若干 CC，在差分结构中对每个 CC 的进入时间 L 查询前缀和。
同样，由于同一个 AA 可能对应多个 CC，所以 QueryCC(u) 需要把所有对应的 CC 都查询一遍。

void QueryCC(int u) {
  for (auto [v, qidx] : querys[u]) {
    const int L2 = in[v];
    ans[qidx] = fenwick.Query(L2);  // 求前缀和
  }
}

每个分组的主函数只需要调用上面的两个 DFS 即可。

void Solver(GroupInfo& groupInfo) {  //
  Dfs2(groupInfo.trie2.root_index, groupInfo.trie2.dfs_index);
  fenwick.Init(groupInfo.trie2.dfs_index + 3);
  Dfs1(groupInfo.trie1.root_index);
}

八、复杂度分析

设插入到两棵 Trie 的所有字符串总长度为 L，对应的 Trie 总节点数为 N（通常 N = O(L)）。
构建与一次完整的 DFS 遍历为 O(N)；若采用 26 分支的定长数组实现，循环 26 带来的仅是常数因子。

Dfs2 遍历 Trie2 并建立 DFS 序，复杂度 O(N)；树状数组/线段树初始化 O(N)。
Dfs1 遍历 Trie1 为 O(N)；期间对每个加入/删除的 C 做两次差分（Fenwick.Add），以及对每个查询做一次前缀和（Fenwick.Query），合计 O((K + Q) log N)，其中 K 为加入/删除操作总次数，Q 为查询总次数。

综合来看，时间复杂度 O(N + (K + Q) log N)，常数因子（如 26）可视为 log ；在典型数据下可记为 O(N log N)。

九、总结

本文介绍了 CSP-S 2025 第三题“谐音替换”的字典树 Trie 解法。
通过结合区间覆盖点、树上路径、扫描线、树递归栈等前置知识，成功将问题转化为树上路径问题。
最后利用差分线段树或树状数组，成功解决了动态更新和查询的树上路径问题。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code