CSP-J 2025 完整版题解（含源码与官方测试数据）

零、背景

CSP 的官方测试数据终于出来了。上篇文章已经分享了《CSP-S 2025 完整版题解》，这里分享 CSP-J 的完整版题解。

PS：CSP-J 和 CSP-S 的题目与所有官方测试数据已经上传到网盘，各种题解的源码也已整理上传。有需要的同学可关注公众号，回复 CSP-2025 获取。
PS2：感谢 Devil 私信提醒我 CSP-S 最后一题上传的代码不全，现已补充完整。

阅读指引：本文按每道题给出「题意→多种算法思路→复杂度与得分→小结图」，必要处补上符号约定与动机，便于完整复现与对比优化路径。

一、拼数（number）

题目：给一个至少包含一个正整数的字符串，问选择一些数字，可以组成的最大数是多少？

思路：不管数据范围多大，核心算法都一样：先过滤出数字，再对数字做逆序排序。

特殊性质 A：仅包含数字。
这一点其实不影响整体思路；先用一层循环过滤出数字，这是编程的入门基础。

算法1：手写冒泡或插入排序。
复杂度：O(n^2)。
得分：72 分

算法2：使用 STL 自带排序。
复杂度：O(n log n)。
得分：100 分

算法3：计数排序。

思路：小学六年级或者初一的娃，可能还不会手写排序算法，但会数数。
我们可以开一个大小为 10 的数组 cnt，遍历字符串时，遇到数字就将对应的 cnt 下标加一。
最后从 9 到 0 遍历 cnt 数组，输出对应数字即可。

复杂度：O(n)。
得分：100 分

总结

二、座位（seat）

题意：给你 n×m 个学生乱序的成绩表，其中每个学生有一个独一无二的成绩。
现在要把学生按成绩从高到低排成 n 行 m 列的座位表。
要求 S 形排列，即第一列从上到下，第二列从下到上，第三列从上到下，依此类推。
问成绩表中第一个学生在排好序的座位表中处于什么位置？

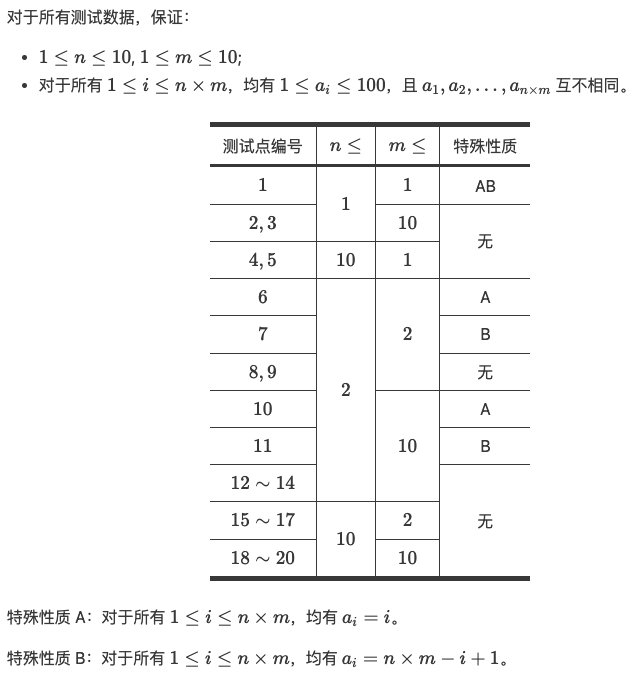
算法1：特殊性质 A：顺序 1～n×m
思路：成绩在最后一名，处于 S 形排列的最后一个位置。
根据奇偶性判断最后一列是从上到下还是从下到上，计算出位置。
复杂度：O(nm)。
得分：15 分

算法2：特殊性质 B：逆序 n×m～1
思路：成绩在第一名，处于 S 形排列的第一个位置，输出 (1,1)。
复杂度：O(nm)。
得分：25 分

算法3：计数排序 + 模拟

思路：对于不会排序的同学，可以参考第一题的计数排序。
我们可以开一个大小为 101 的数组 cnt，遍历成绩表时，遇到成绩就将对应的 cnt 下标加一。
最后从大到小遍历 cnt 数组，从而得到逆序序列。

复杂度：O(nm)。
得分：100 分

算法4：STL 排序 + 模拟
思路：直接使用 STL 排序，然后模拟 S 形排列。
复杂度：O(nm log(nm))。
得分：100 分

算法5：STL 排序 + 定位排名 + 数学法
思路：一列有 n 个学生，知道排名后，就可以定位到第几列；
再根据列数的奇偶性，计算在该列的第几行。
复杂度：O(nm log(nm))。
得分：100 分

总结

PS：可以发现，即使你不会手写排序算法，也可以用“计数”的办法拿到满分。
注意事项：先输出列号，再输出行号。

三、异或和（xor）

题意：给定一个非负整数序列，问能选择多少个互不重叠的子区间，使得每个子区间的异或值都等于 K。

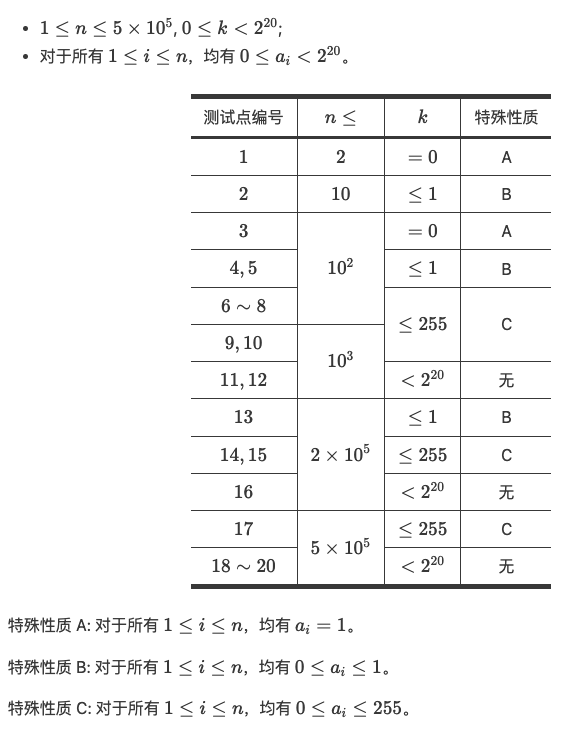
算法1：特殊性质 A：所有 a_i = 1 且 k = 0
思路：2个可以组成一个异或和为 0 的子区间。
因此，答案就是 n/2。
复杂度：O(n)。
得分：10 分

算法2：特殊性质 B：a_i ∈ {0,1} 且 k ∈ {0,1}

思路：记录最后一次 1 出现的位置 p1，然后分四种情况讨论。

1）v=0 k=0时，dp[i] = dp[i-1] + 1
2）v=0 k=1时，dp[i] = max(dp[i-1], dp[p1-1] + 1)
3）v=1 k=0时，dp[i] = max(dp[i-1], dp[p1-1] + 1)
4）v=1 k=1时，dp[i] = dp[i-1] + 1

总结四种情况的规律，可以发现当 v 与 k 相同时，答案是 dp[i-1] + 1；否则答案是 max(dp[i-1], dp[p1-1] + 1)。
所以可以简化合并。

if (v == k) {
  dp[i] = dp[i - 1] + 1;
} else {
  if (lastOne != -1) {
    dp[i] = max(dp[i - 1], dp[lastOne - 1] + 1);
  } else {
    dp[i] = dp[i - 1];
  }
}

复杂度：O(n)。
得分：30 分

算法3：动态规划，暴力找最近满足要求的区间
思路：算法2 由于 0/1 的特殊性质，可以直接记录最后一个 1 出现的位置，从而直接找到满足要求的区间。
但如果数字不止 0/1 呢？
最直接的想法是从后到前暴力查找最近满足要求的区间。
复杂度：O(n^2)。
得分：70 分

算法4：特殊性质 C：0 ≤ a_i ≤ 255

思路：可能你想到了通过两个前缀异或值的关系来找到满足要求的区间。
但前缀异或值的范围可能很大；没学过 STL 不会unordered_map，也可能不清楚 2^20 是否能直接开数组存下。
这里有个特殊性质 C：0 ≤ a_i ≤ 255，于是前缀异或值也落在 0～255。
因此，可以开一个大小为 256 的数组 lastIndex，记录每个前缀异或值对应的最近下标。

复杂度：O(n)。
得分：80 分

算法5：前缀和 + 开大数组
思路：如果明确知道 2^20 可以存下前缀异或的所有可能值，就直接开一个大小为 2^20 的数组 lastIndex，记录每个前缀异或值对应的最近下标。
复杂度：O(n)。
得分：100 分

算法6：前缀和 + 哈希表
思路：如果不确定 2^20 是否能存下所有可能的前缀异或值，可以使用 unordered_map 来记录每个前缀异或值对应的最近下标。
复杂度：O(n)。
得分：100 分

总结

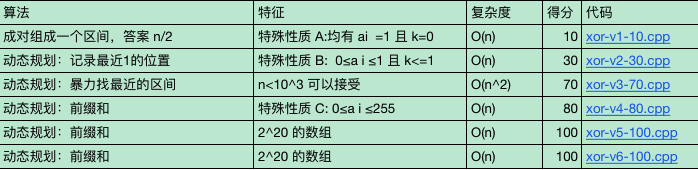
四、多边形（polygon）

题意：给一些木棍，选择若干根组成多边形，问有多少种不同的选择方案。

前置思路

题目已给出判定条件：边数 ≥ 3 且所有选中木棍的总长度 > 最长木棍长度的两倍。
等价于：所选集合中，最长木棍的长度 < 其余木棍长度之和。
因此可先排序，再考虑如何计数。

算法1：所有木棍长度均为 1
思路：只要选择的根数 ≥ 3 就满足要求；因此用总方案数减去不满足的情况。
公式：2^n - C(n,0) - C(n, 1) - C(n, 2)
复杂度：O(n)。
得分：24 分

算法2：0/1 背包 DP

思路：dp[i][j] 表示前 i 根木棍中，选取一些木棍使得长度和为 j 的方案数。
若第 i 根木棍当“最长木棍”，则可与“前 i-1 根的子集和 V”配对，且需满足 V > a[i]，方案数为 sum(dp[i-1][V])。

如何求 dp[i][j]呢？
对于第 i 个木棍，有两种选择，选或者不选。
故状态转移：dp[i][j] = dp[i-1][j] + dp[i-1][j - a[i]]。

此时，长度和 j 的上界为所有木棍的总长度 S = sum(a)。
复杂度：O(n · S)。
得分：80 分

ll ans = 0;
ll sumV = n * maxV;
vector<ll> dp(sumV + 1, 0);     // 子集和为 dp[i] 的方案数
dp[0] = 1;                      // 空集
for (int i = 1; i <= n; i++) {  // a[i] 作为最大边
  const ll v = a[i - 1];
  for (int V = v + 1; V <= sumV; V++) {
    ans = (ans + dp[V]) % modV;
  }
  for (int V = sumV; V >= v; V--) {
    dp[V] = (dp[V - v] + dp[V]) % modV;
  }
}

算法3：截断背包（压桶合并大数）

思路：仍是上面的 DP 思路，目标是求 sum(dp[i-1][V])，其条件为 V > a[i]。
注意到 a[i] ≤ 5000，当 V > 5000 时均等价地“满足要求”。
于是可以把所有超过阈值的和统一压到一个“溢出桶”（代码中可用 min(V+v, maxV) 实现），把状态数量截断到常数级阈值范围。

复杂度：O(n · 5001)。
得分：100 分

ll ans = 0;
vector<ll> dp(maxV + 1, 0);     // 子集和为 dp[i] 的方案数
dp[0] = 1;                      // 空集
for (int i = 1; i <= n; i++) {  // a[i] 作为最大边
  const ll v = a[i - 1];
  for (int V = v + 1; V <= maxV; V++) {
    ans = (ans + dp[V]) % modV;
  }
  for (int V = maxV; V >= 0; V--) {
    const ll sum = min(V + v, maxV);
    dp[sum] = (dp[sum] + dp[V]) % modV;
  }
}

算法4：正难则反

思路：求“满足”的方案数较难，不妨先求“不满足”的方案数，再用总方案数相减。
不满足即：“最长木棍长度 ≥ 其他木棍长度之和”。

状态与转移与上面一致，只是这里统计的是“不满足”的情况。对每一根当前当作最长边的木棍，其可搭配的子集和需满足 V ≤ a[i]。
因此，只需累加到对应阈值即可。

ll isNotAns = 0;
vector<ll> dp(maxV + 1, 0);     // 子集和为 dp[i] 的方案数
dp[0] = 1;                      // 空集
for (int i = 1; i <= n; i++) {  // a[i] 作为最大边
  const ll v = a[i - 1];
  // 第 i 条边作为最大边，前面的边的子集和 小于等于 V 的个数
  for (int V = 0; V <= v; V++) {
    isNotAns = (isNotAns + dp[V]) % modV;
  }
  // 第 i 条边加入子集
  for (int V = maxV; V >= v; V--) {
    dp[V] = (dp[V - v] + dp[V]) % modV;
  }
}

总方案数为 C(n,1) + C(n,2) + ... + C(n,n) = 2^n - 1。
所以最终答案就是总方案数减去不满足要求的方案数。

// 答案是 2^n - ans
ll total = 1;
for (int i = 0; i < n; i++) {
  total = (total * 2) % modV;
}
isNotAns = (isNotAns + 1 + modV) % modV;  //  C(n, 0) 空集也算一个
ll ans = (total - isNotAns + modV) % modV;

总结

五、最后

以上就是 2025 年 CSP-J 第二轮算法比赛的全部题解。

这次比赛整体难度不高：
第一题：普及−，计数排序，基本都能拿满分。
第二题：普及−，计数排序 + 模拟/数学计算，基本都能拿满分。
第三题：普及/提高−，即便不会动态规划，合理分值也能到 70 分左右。
第四题：普及/提高−，0/1 背包；即便不会背包，特殊情形也能拿到 24 分。

这样看来，今年 CSP-J 的分数线应该会比较高。

但考虑到大部分同学不一定会去“凑分”，294 分更像是一等的门槛水平。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code