NOIP 2024 第一题 编辑字符串 题解

零、背景

之前已经分享了历年 CSP-J/S 的比赛题解。

今天开始，分享 NOIP 比赛题解。
为了避免四道题放在一篇导致文章过长，我计划每道题单独写一篇，最后再给出一个总结。

这篇文章分享 NOIP 2024 第一道题「编辑字符串」的题解。

PS：源码已上传网盘，公众号回复 NOIP 获取。

一、题目

给两个长度为 n 且字符集为 0 与 1 的二元组字符串 S 和 T。
T 的值为 0 时，代表 S 对应位置的字符是不能动的。
T 的值为 1 时，代表 S 对应位置的字符是可以参与交换的。
交换规则：如果相邻两个字符都是可以交换，则可以进行任意次交换。

现在给你两个二元组字符串 <S0, T0> 和 <S1, T1>。
在分别按照各自的 T 规则进行任意合法交换后，问 S0 与 S1 最多有多少个位置值相同。

等价理解：对每个 T 中连续为 1 的区间 [L, R]，S 在该区间内可以任意重排（只看区间内 0/1 的数量即可）；T 为 0 的位置则固定不可动。

二、算法分析

先看数据范围与特判情形，分为五类：

1）n <= 10
2）特殊性质 A：S0 的所有字符都相同
3）特殊性质 B：T0 = T1
4）特殊性质 C：T0 与 T1 各自恰好只有一个字符为 0
5）一般情形（随机输入）

下面分别说明这些情形的处理方式，并逐步归纳到通用贪心。

假设没有交换限制

如果整个区间都可交换，那么只需要贪心：统计 S0 与 S1 中相同字符的总数即可（本质是按字符计数匹配）。
复杂度：O(n)

数据范围 n <= 10

可以暴力枚举。
2^10 最多是 1024 种，对两个字符串分别枚举所有重排情况，取最大相同字符数。
复杂度：O(2^n * 2^n)

考虑到存在 T=0 的不可交换位置，实际上每段需要独立枚举，复杂度会更低。

特殊性质 A

若 S0 的所有字符都相同，则不管怎么交换，S0 不会改变；此时 S1 在任意重排后，与 S0 位置相同的字符也不变。
因此直接统计 S1 中与 S0 字符相同的个数即可。
复杂度：O(n)

特殊性质 B

当 T0 = T1，两者可任意交换的连续区间完全一致。
我们对每个连续区间独立处理，按计数贪心统计该区间内 S0 与 S1 能匹配的相同字符总数。
复杂度：O(n)

特殊性质 C

当 T0 与 T1 各自恰好只有一个 0 时，可根据两个 0 的位置将字符串划分成若干子串：

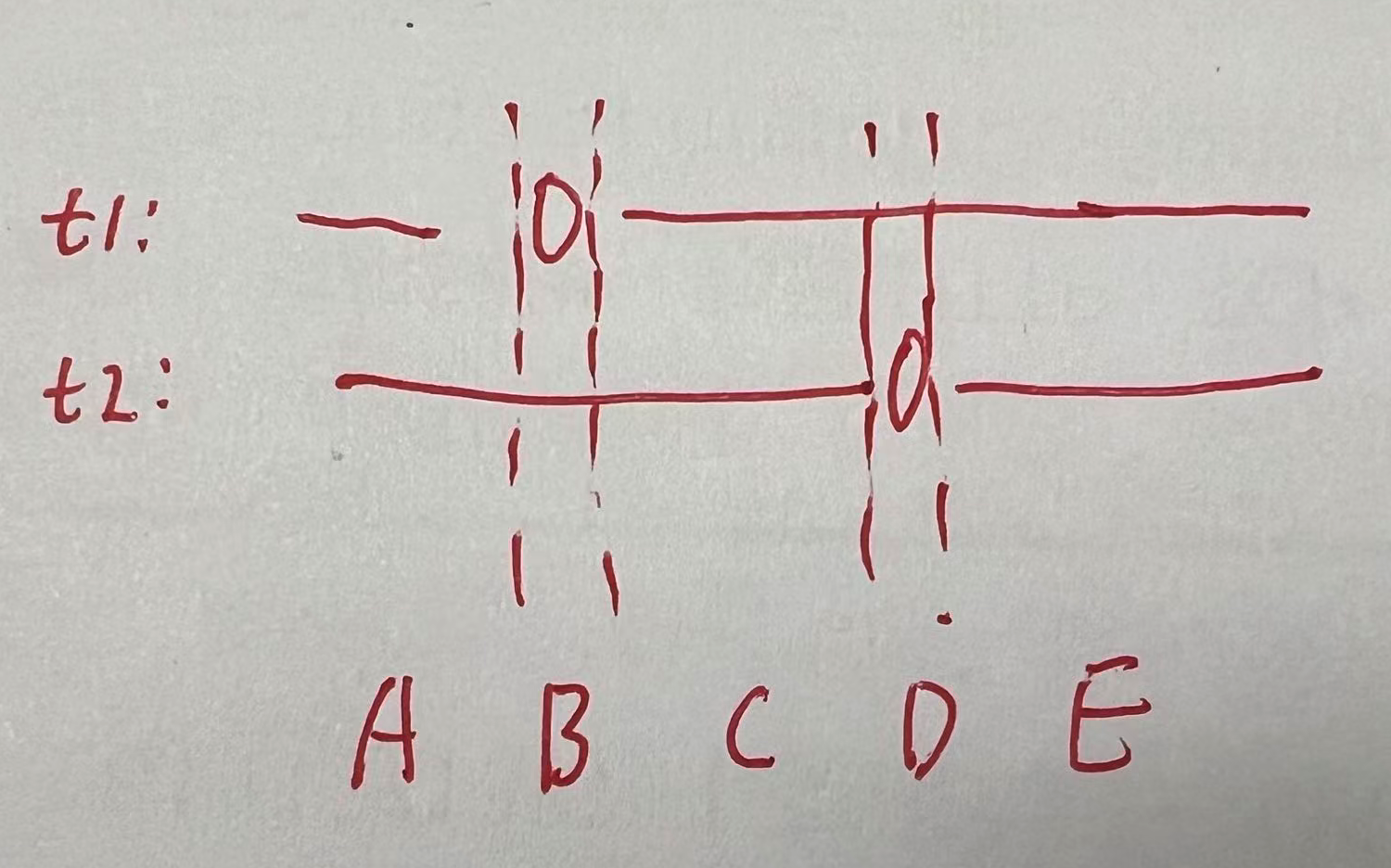
一种自然的贪心是：用较短的可交换子串去匹配较长子串中的字符集合。
例如，用 T0 的 0 之前的子串 A 去匹配 T1 的 ABC，尽可能匹配 A 的字符数；

然后用剩余字符去匹配 T0 的那个不可交换位置；
再用 T1 的 ABC 剩余字符集合去匹配 T0 的后续集合 CDE。
这个过程是递归/迭代式的：始终让“短串优先匹配长串”，并在每次匹配后删空已用完的段。

这个思路可以推广到存在任意多个 0 的场景。

一般情形（无特殊性质）

由对特殊性质 C 的分析可知，“按 0 将序列切段 + 短串优先匹配长串”的贪心，适用于任意多个 0 的情况。
因此在一般情形下也可直接采用该贪心。

三、代码实现

根据贪心过程，需要先依据 T 中 0 的位置把字符串切分为若干子串。
对子串我们只关心字符计数（0/1 的数量）。
其中，T=0 的位置视为长度为 1 的不可交换子串；连续 T=1 的区间视为一个可交换子串。

struct Node {
  int type;        // TYPE_CONST 或 TYPE_SWAP
  int v[2] = {0, 0}; // 记录 0/1 计数
};
void Init(vector<Node>& nodes, char* s, char* t) {
  nodes.clear();
  nodes.push_back(Node(TYPE_CONST, 0));  // 哨兵，避免边界判断
  for (int i = 0; i < n; i++) {
    const int type = t[i] - '0';
    const int val = s[i] - '0';
    if (type == TYPE_CONST) {
      nodes.push_back(Node(TYPE_CONST, val));
    } else {
      if (nodes.back().type == TYPE_SWAP) {
        nodes.back().Add(val);
      } else {
        nodes.push_back(Node(TYPE_SWAP, val));
      }
    }
  }
}

之后采用“短串优先匹配长串”的步骤：枚举当前较短的尾部子串，尝试在较长子串中匹配字符。

int p0 = 0, p1 = 1;
if (nodes[p0].back().Size() > nodes[p1].back().Size()) {
  swap(p0, p1);
}
// 大的匹配小的
int v = 0;
if (!nodes[p0].back().TryPop(v)) {
  v = 1 - v;
}
if (nodes[p1].back().TryPop(v)) {
  ans++;
}

每次匹配后都要检查子串是否已空，为空则删除：

// 删除空的区间
for (int i = 0; i < 2; i++) {
  if (nodes[i].back().Size() == 0) {
    nodes[i].pop_back();
  }
}

整体代码量不大，思路也较清晰。

实现小技巧：

• 不可交换的位置视为长度为 1 的子串；
• 始终让短子串去匹配长子串；

这样实现过程中不需要额外判断“是否为不可交换字符”以及“谁长谁短”。

如果不进行封装，会出现大量分支。建议封装 MergeConstSwap 和 MergeSwapSwap 两个函数，避免冗长的 if/else：

if (nodes1.back().type == TYPE_CONST && nodes2.back().type == TYPE_CONST) {
  if (nodes1.back().val == nodes2.back().val) {
    ans++;
  }
  nodes1.pop_back();
  nodes2.pop_back();
} else if (nodes1.back().type == TYPE_CONST) {  // nodes2 swap
  MergeConstSwap(nodes1, nodes2);
} else if (nodes2.back().type == TYPE_CONST) {  // nodes1 swap
  MergeConstSwap(nodes2, nodes1);
} else {  // swap swap
  if (nodes1.back().Size() > nodes2.back().Size()) {
    MergeSwapSwap(nodes2, nodes1);
  } else {
    MergeSwapSwap(nodes1, nodes2);
  }
}

四、总结

这道题核心在于“按 0 切段 + 在每一步让短子串优先匹配长子串”的贪心。
在分析特殊性质 C 的过程中即可推导出这一思路，且它自然推广到任意多个 0 的一般情形。
实现层面，把 T=0 的位置视为长度 1 的区间，有助于统一处理逻辑，使代码更为简洁。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code