动态规划详解：掩码子集问题

零、背景

二进制的子集问题，是动态规划中的一类重要问题。

最近在做算法比赛的时候，遇到了多次子集相关的问题，所以写一篇总结。

本文主要围绕「位运算 + 状压 DP」这一条主线，依次讲四个常见场景：

• 枚举子集
• 子集容斥
• 子集最大值
• 子集和（Sum Over Subsets，SOS DP）

希望看完之后，你在遇到「二进制 + 子集」类的题目时，可以有一个比较完整的套路。

一、枚举子集

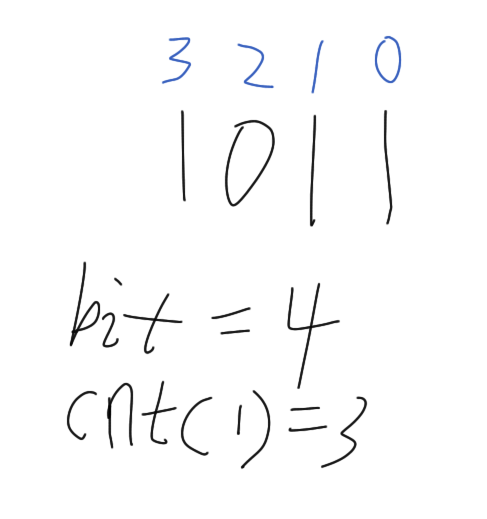
如上图，给一个掩码 1011，总位数为 n = 4，其中有 k = 3 个 1。
这里的 k 一般用来表示「1 的个数（置位数）」，后面复杂度里的 2^k 就是指「只和这些 1 所在的位有关」。

最朴素的做法是枚举所有 n 位的二进制数，然后判断它是不是 mask 的子集：

1）枚举所有 0 ~ (1<<n)-1；
2）对每个 i，用 (i & mask) == i 判断它是否是 mask 的子集。

复杂度：O(2^n)

for (int i = 0; i < (1 << n); i++) {
  if ((i & mask) == i) {
    printf("%d\n", i);
  }
}

而更优的方式是利用位运算，直接在「mask 的所有子集」之间跳转，从一个子集快速到下一个子集。

1）从 sub = mask 开始；
2）不断做 sub = (sub - 1) & mask，就能枚举完所有非空子集。

复杂度：O(2^k)

const int mask = 0b1011;
for (int sub = mask; sub; sub = (sub - 1) & mask) {
  printf("%d\n", sub);
}

二、子集容斥

子集容斥可以理解为：对普通容斥（选 / 不选某个元素）做了一次「状态压缩」。

• 有 n 个元素，每个元素对应一位 bit；
• 我们考虑所有 bit 的「选 / 不选」组合；
• 每一种组合对应一个子集，它对答案有一个贡献。

对于所有单个 bit，我们先分别算出它们的贡献。

之后会发现：
两个 bit 一起选的时候，被算了两次，需要减掉；
三个 bit 一起选的时候，被多减了一次，需要加回来；

总结下来就是：
选中 bit 个数为奇数，加；
选中 bit 个数为偶数，减。

有了这个规律之后，就可以「枚举所有子集」，然后按子集的 1 的个数决定是加还是减：

for (int sub = mask; sub; sub = (sub - 1) & mask) {
  ll oneCount = __builtin_popcount(sub);
  if (oneCount % 2 == 1) {
    ans = (ans + SolverSub(sub)) % mod;
  } else {
    ans = (ans - SolverSub(sub) + mod) % mod;
  }
}

这里的 SolverSub(sub) 表示「只选中 sub 这些 bit 时，对答案的贡献」，具体怎么算由题目决定。

这一节和上一节的关系是：
第一节教你「怎么枚举所有子集」；
这一节告诉你「在所有子集上做容斥计算」的一个常见模式。

三、子集最大值

《LeetCode 第 465 场算法比赛》的第三题，转化之后，可以看成一个「二进制子集最大值」问题。

子集最大值是一个非常经典的状态压缩 DP 模板。
大致意思是：

设 dp[mask] 表示子集 mask 的答案；
我们希望让 dp[mask] 变成「所有子集中的最大值」；
也就是「把一个子集，按 bit 拆成若干更小的子问题」，然后在这些子问题的答案中取最大值。

有两种常见的写法：

1）当前代码写法：枚举一个「子问题」有哪些「父问题」，并更新父问题的最大值。

const int MaxBitVal = 1 << maxBit;
for (auto v : nums) {
  dp[v] = v;
}
for (int i = 0; i < MaxBitVal; i++) {
  for (int j = 0; j < maxBit; j++) {
    dp[i | (1 << j)] = max(dp[i | (1 << j)], dp[i]);
  }
}

这里的含义是：

枚举所有较小的 i；
把 i 的答案「推」到所有只多了一个 bit 的父集合 i | (1<<j) 上；
最终，每个 mask 都能拿到所有子集里的最大值。

2）更标准、更直观的写法：枚举一个「父问题」有哪些「子问题」，并从子问题中取最大值。

for (int i = 0; i < MaxBitVal; i++) {
  for (int j = 0; j < maxBit; j++) {
    if (i & (1 << j)){
      dp[i] = max(dp[i], dp[i ^ (1 << j)]);
    }
  }
}

具体含义是：
对于每个 mask，枚举它每一位为 1 的 bit；
把这个 bit 去掉得到更小的子集 mask ^ (1<<j)；
在这些子集中取最大值。

两种写法本质上是同一个 DP 思想：
要么从「小集合推到大集合」；
要么从「大集合从子集中取最大值」。

四、子集和

《LeetCode 第 477 场算法比赛》的第四题，问题转化之后，变成了求二进制子集的和。

子集和问题也是一个典型的状态压缩 DP，不过比「子集最大值」稍微复杂一些。

如果你按前一节的思路，直接按照 bit 拆分子问题，很快就会发现：会出现大量重复子问题；

如下图所示，如果我们「随便拆」子问题，会出现许多交叉和重叠。

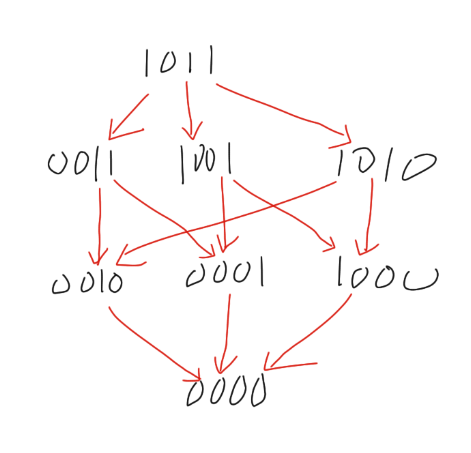
为了解决这个问题，我们需要「有策略地拆分子问题」，让子问题之间没有交集。

一种显然的策略是：按前缀来划分。

例如，对于 01011，我们可以先对最高位的 1 进行划分：

1）划分为 01011，且前缀必须包含 01；
2）划分为 00011，且前缀必须包含 00；

两个划分的后缀都相同，都是 011，但是由于前缀不同，所以它们是不同的子问题。
这个过程是递归的，每递归一次，前缀长度增加 1。
到叶子节点的时候，就划分出所有子问题。

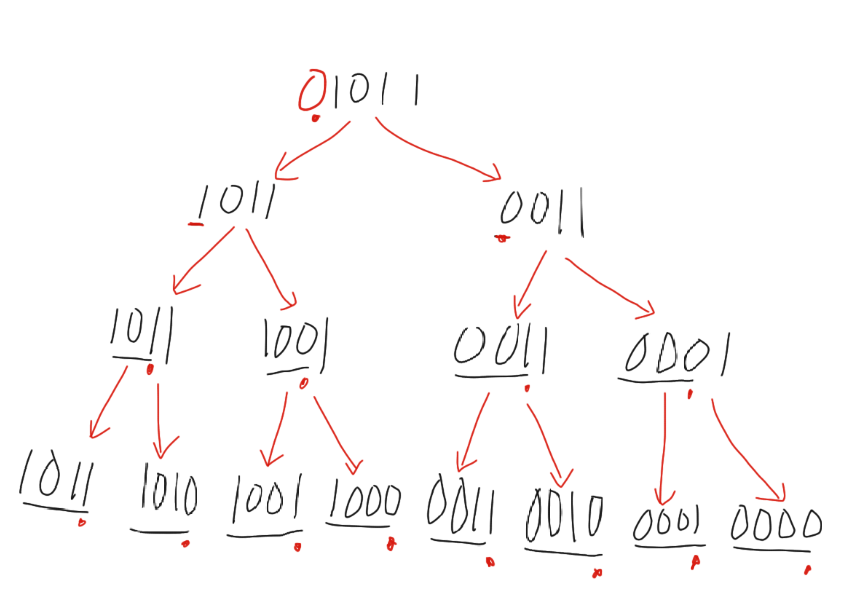
根据这个划分，我们可以定义状态：
f(i, mask) 表示：从第 i 位及更高位已经固定时，mask 的子集和。

状态转移方程如下：

// 前提: mask & (1 << i) != 0
f(i + 1, mask) = f(i, mask) + f(i, mask ^ (1 << i));

含义是：
对第 i 位为 1 的情况： 要么这一位在子集中选（对应 mask）；
要么这一位在子集中不选（对应 mask ^ (1<<i)）；

两种情况的贡献相加，就得到更高一层的结果。

完整的二维 DP 写法如下：

vector<vector<ll>> dp(kMaxBit + 1, vector<ll>(kMaxMask, 0));
for (ll x : nums) {
  dp[0][x]++;
}
for (int i = 0; i < kMaxBit; i++) {
  for (int mask = 0; mask < kMaxMask; mask++) {
    if (mask & (1 << i)) {
      dp[i + 1][mask] = dp[i][mask] + dp[i][mask ^ (1 << i)];
    } else {
      dp[i + 1][mask] = dp[i][mask];
    }
  }
}

可以看到：
dp[i + 1][mask] 只依赖 dp[i][mask] 和 dp[i][mask ^ (1 << i)]；
mask 这一维只会依赖到一个更小的 mask ^ (1 << i)。

因此，我们可以在第二维上做空间压缩，把二维 DP 压成一维：
用一个 dp[mask] 表示当前层的结果；
按 bit 一层一层地更新它。

for (int i = 0; i < kMaxBit; i++) {
  for (int mask = kMaxMask - 1; mask >= 0; mask--) {
    if (mask & (1 << i)) {
      dp[mask] += dp[mask ^ (1 << i)];
    }
  }
}

从依赖关系可以看出：
每一层的转移，都是把一个当前 Bit 位无关的掩码加到当前 Bit 位有关的掩码；
因此遍历顺序实际上并不影响正确性。

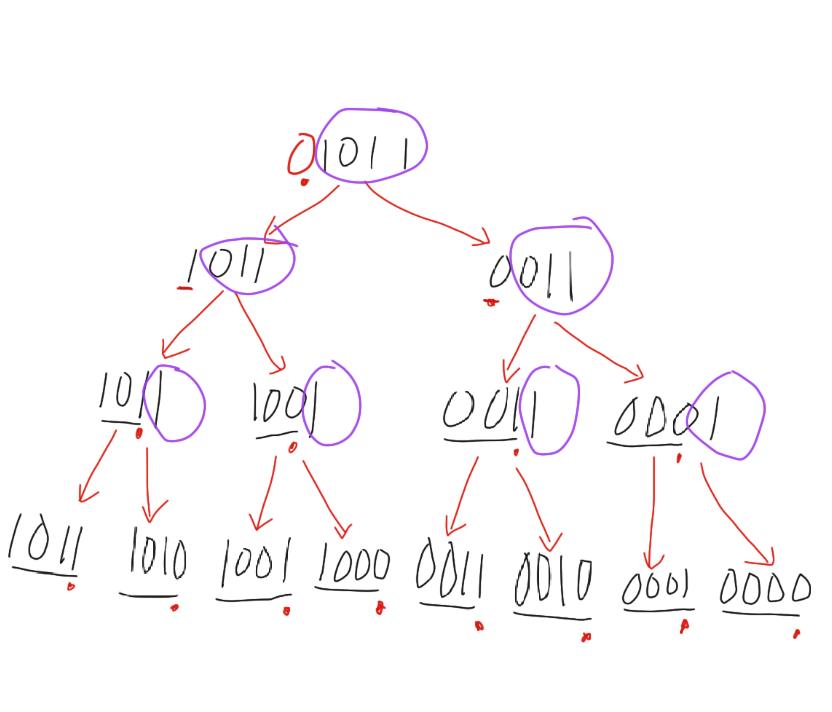
用图再看一次，会比较直观：

在这棵二叉树中，每个节点有两个儿子：
一个儿子是「值不变」的自己；
另一个儿子是「去掉当前 bit」之后的更小值。

由于更小的值在这一层不满足 mask & (1 << i)，这一层不会对它进行运算。
所以枚举顺序可以是任意的，例如：

for (int i = 0; i < kMaxBit; i++) {
  for (int mask = 0; mask < kMaxMask; mask++) {
    if (mask & (1 << i)) {
      dp[mask] += dp[mask ^ (1 << i)];
    }
  }
}

这正是经典的 Sum Over Subsets（SOS DP）/ 高维前缀和 模板写法。
复杂度是 O(k * 2^k)。

为了进一步提高性能，还可以只枚举「总体 OR 掩码」 preOr 的子集：

for (int i = 0; i < kMaxBit; i++) {
  if ((preOr & (1 << i)) == 0) continue;
  for (int mask = preOr; mask; mask = (mask - 1) & preOr) {
    if (mask & (1 << i)) {
      dp[mask] += dp[mask ^ (1 << i)];
    }
  }
}

这里利用了第一节的「枚举子集」技巧，把不可能出现的 mask 直接跳过。

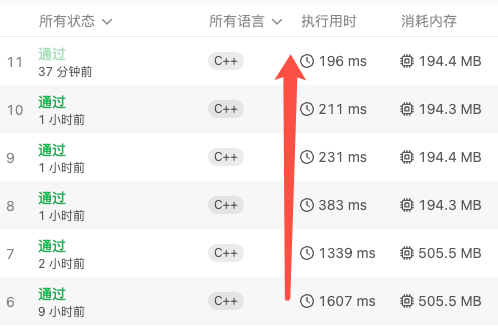
随着一步步优化，耗时也从 1607ms 降低到了 196ms。

五、最后

好了，这篇文章分享了：

• 枚举子集的高效模板；
• 子集容斥的经典写法；
• 子集最大值的两种等价 DP 实现；
• 子集和（SOS DP / 高维前缀和）的状态设计与优化。

尤其是子集和部分，对应的标准名字叫做 Sum Over Subsets，简称 SOS，对应的算法通常被称作「高维前缀和」。

不过，即使你暂时不熟悉 SOS DP 的术语，只要理解了「划分出不重叠的子问题」这个思路，用一个二维 DP 也能把问题解决；在此基础上，再做空间压缩和枚举优化即可。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code