NOIP 2025 pdf 题目分享

零、背景

今天下午拿到了 NOIP 2025 的真题。
不过当时在外面，所以没来得及写题解。
这里先分享一下真题。

PS：题目pdf 已上传网盘，公众号回复 NOIP-2025 获取。

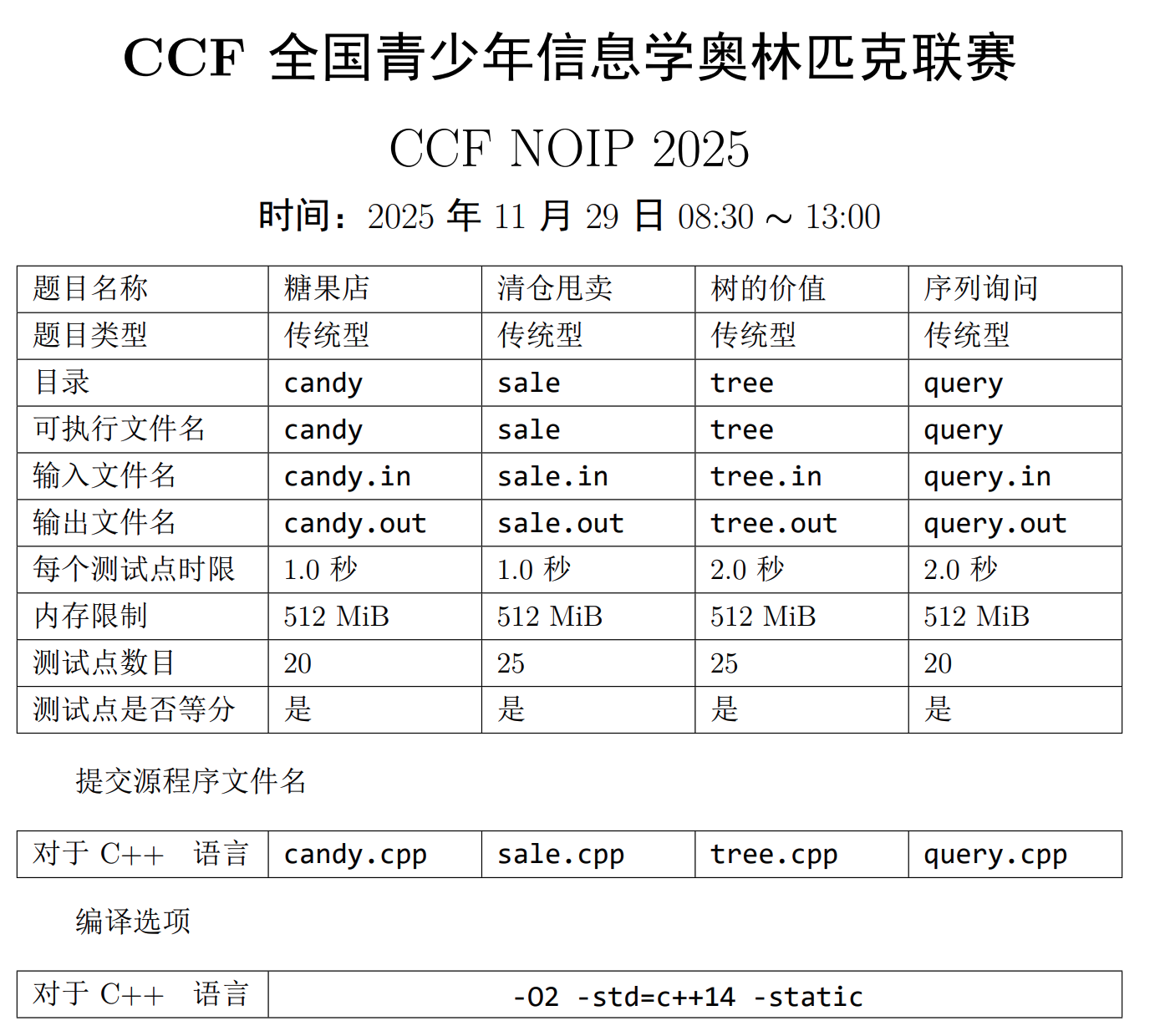
一、糖果店（candy）

小 X 开了一家糖果店，售卖 n 种糖果，每种糖果均有无限颗。

对于不同种类的糖果，小 X 采用了不同的促销策略。
具体地，对于第 i (1 ≤ i ≤ n) 种糖果，购买第一颗的价格为 xi 元，第二颗为 yi 元，第三颗又变回 xi 元，第四颗则为 yi 元，以此类推。

小 R 带了 m 元钱买糖果。
小 R 不关心糖果的种类，只想得到数量尽可能多的糖果。

你需要帮助小 R 求出，m 元钱能购买的糖果数量的最大值。

二、清仓甩卖（sale）

小 X 的糖果促销策略很成功，现在糖果店只剩下了 n 颗糖果，其中第 i (1 ≤ i ≤ n)颗糖果的原价为 ai 元。
小 X 计划将它们全部重新定价，清仓甩卖。

具体地，小 X 会将每颗糖果的清仓价格分别定为 1 元或 2 元。
设第 i (1 ≤ i ≤ n) 颗糖果的清仓价格为 wi ∈ {1, 2} 元，则它的性价比被定义为原价与清仓价格的比值，即 ai/wi。

小 R 又带了 m 元钱买糖果。
这一次，小 R 希望他购买到的糖果的原价总和最大，于是他采用了以下购买策略：将所有糖果按照性价比从大到小排序，然后依次考虑每一颗糖果。

具体地，若小 R 在考虑第 i (1 ≤ i ≤ n) 颗糖果时剩余的钱至少为 wi 元，则他会购买这颗糖果，否则他会跳过这颗糖果，继续考虑下一颗。
特别地，若存在两颗糖果的性价比相同，则小 R 会先考虑原价较高的糖果；
若存在两颗糖果的性价比与原价均相同，则小 R 会先考虑编号较小的糖果。

例如，若小 X 的糖果商店剩余 3 颗糖果，原价分别为 a1 = 1，a2 = 3，a3 = 5，而清仓价格分别为 w1 = w2 = 1，w3 = 2，则性价比分别为 1, 3,5/2。
因此小 R 会先考虑第2 颗糖果，然后考虑第 3 颗糖果，最后考虑第 1 颗糖果。

小 R 想知道，在小 X 的所有 2n 种定价方案中，有多少种定价方案使得他按照上述购买策略能购买到的糖果的原价总和最大。
你需要帮助小 R 求出满足要求的定价方案的数量。

由于答案可能较大，你只需要求出答案对 998, 244, 353 取模后的结果。

三、树的价值（tree）

给定一棵 n 个结点的有根树，其中结点 1 为根，结点 i (2 ≤ i ≤ n) 的父亲结点为结点 pi。

对于 1 ≤ i ≤ n，定义结点 i 的深度 di 为结点 1 到结点 i 的简单路径的边数，也就是说，d1 = 0，di = dpi + 1 (2 ≤ i ≤ n)。
定义有根树的高度 h 为所有结点的深度的最大值，即 h = max(di)。
给定高度的上界 m。在本题中，给定的有根树的高度不超过m。

你需要给每个结点设置一个非负整数作为它的权值。
对于 1 ≤ i ≤ n，若结点 i 的权值为 ai，令 Si 表示结点 i 的子树中结点权值构成的集合。

对于每一种权值设置方案，定义树的价值为∑mex(Si)，其中 mex(S) 表示不在集合 S 中的最小非负整数。

例如，在下图中，若设置 a1 = 3，a2 = 2，a3 = a4 = 0，a5 = 1，则 S1 = {0, 1, 2, 3}，S2 = {0, 1, 2}，S3 = {0}，S4 = {0}，S5 = {1}，树的价值为 4 + 3 + 1 + 1 + 0 = 9。

你需要求出，在所有权值设置方案中，树的价值的最大值。

四、序列询问（query）

给定一个长度为 n 的整数序列 a1, a2, . . . , an。

有 q 次询问，其中第 j (1 ≤ j ≤ q) 次询问将会给出 Lj, Rj (1 ≤ Lj ≤ Rj ≤ n)。

定义区间 [l, r] (1 ≤ l ≤ r ≤ n) 是极好的，当且仅当区间 [l, r] 的长度在 [Lj, Rj] 内，即 Lj ≤r−l+1 ≤ Rj。

定义区间 [l, r] (1 ≤ l ≤ r ≤ n) 的权值为∑（ai）。对于所有 i = 1, 2, . . . , n，求出所有包含 i 的极好区间的最大权值。

五、最后

由于现在还没有官方数据，后面我会先出一版题解，官方数据出来后我会再出一版完整版题解。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code