NOIP 2025 第四题 序列询问 几何满分题解

零、背景

之前已经在《PDF 题目分享》中分享了 NOIP 2025 的题目。
在《糖果店 candy 题解》里给出了第一题的题解。
在《清仓甩卖 sale 题解》中给出了第二题的题解。
在《序列询问 query 单调队列 题解》中给出了第四题的单调队列视角题解。
在《序列询问 query 几何图形 题解》中给出了第四题的几何图形视角题解，但最高只得 80 分。

面对一个正确的题解却只得 80 分，我还是有点不甘心。
所以研究了下超时的原因，发现是 RMQ 二维数组的锅，修改后就 100 分了。

PS：题目 PDF、官网测试数据、题解代码已上传网盘，公众号回复 NOIP-2025 获取。
PS2：最近工作上比较忙，所以更新会比较慢，见谅。

一、快速回顾

对于每个位置 i，需要找到覆盖 i 的最大权值的极好区间。

那覆盖 i 的极好区间究竟有哪些呢？

如下图，可以按照区间的右边界进行分组。
以 [i, i+R-L] 为右边界时，长度为 [L, R] 的极好区间都是存在的，即都有 R-L+1 个极好区间。

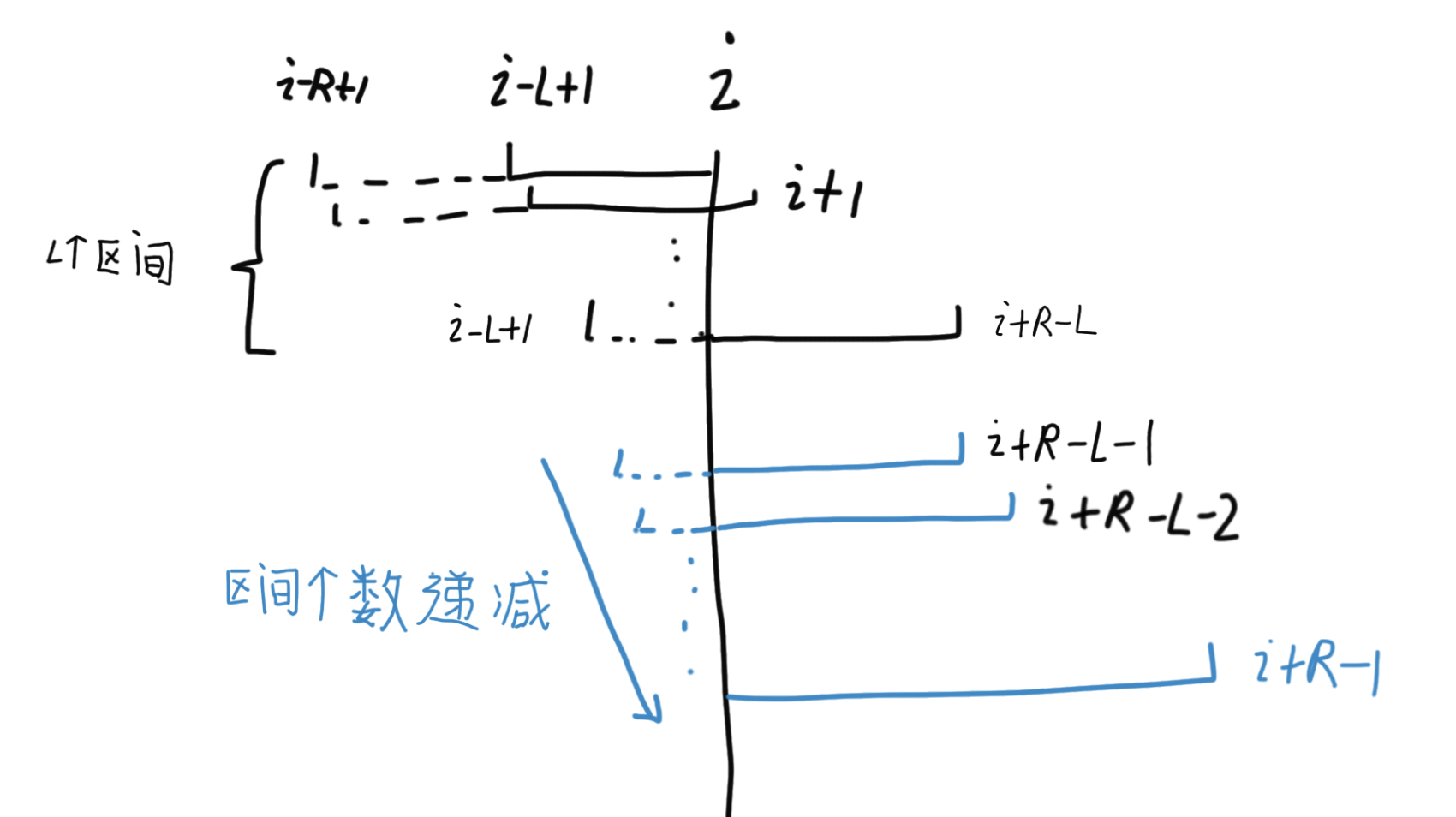
如果把区间 [l, r] 看作二维坐标系中的一个点，其中 l 是横坐标、r 是纵坐标，那么所有满足条件的区间如图所示，会形成一个梯形。

观察梯形的特征，我们可以对这个梯形进行进一步划分，使得若干个简单图形可以完全覆盖整个梯形。

首先是把梯形划分为一个平行四边形和一个等腰直角三角形。

对于这块等腰直角三角形，可以根据中点，将其划分为两个平行四边形和一个正方形。
如下图，粉红色边框的平行四边形、浅蓝色边框的平行四边形、紫色边框的正方形。

对于平行四边形，可以通过单调队列 + RMQ 来快速计算出答案。

而对于中间的正方形，推导的结论就是：只需要求一个区间的最大值减去另一个区间的最小值即可。
区间最大值和最小值依旧可以使用单调队列或者 RMQ 来做。

二、代码优化

前文提到，使用 RMQ 来求最值，只得到 60 分。
再结合特殊性质，最高得到 75 分。

大致算一下常数：预处理最大值和最小值的 RMQ，复杂度是 n log(n)，其实也不算高。
我把 RMQ 全部换成单调队列后，通过的样例反而更少了。

这说明瓶颈不在算法复杂度上，而是在实现细节和常数因子上。
所以，问题出在 RMQ 上。

阅读 oi-wiki 上的 ST 表一节，发现注意事项里提到：建议把幂次作为第一维，把数组大小作为第二维。
这背后的原因也很简单：最低维在内存中是连续的，CPU 会一次性把这一整段连续空间加载到缓存中，根据局部性原理，就能明显减少访存开销。

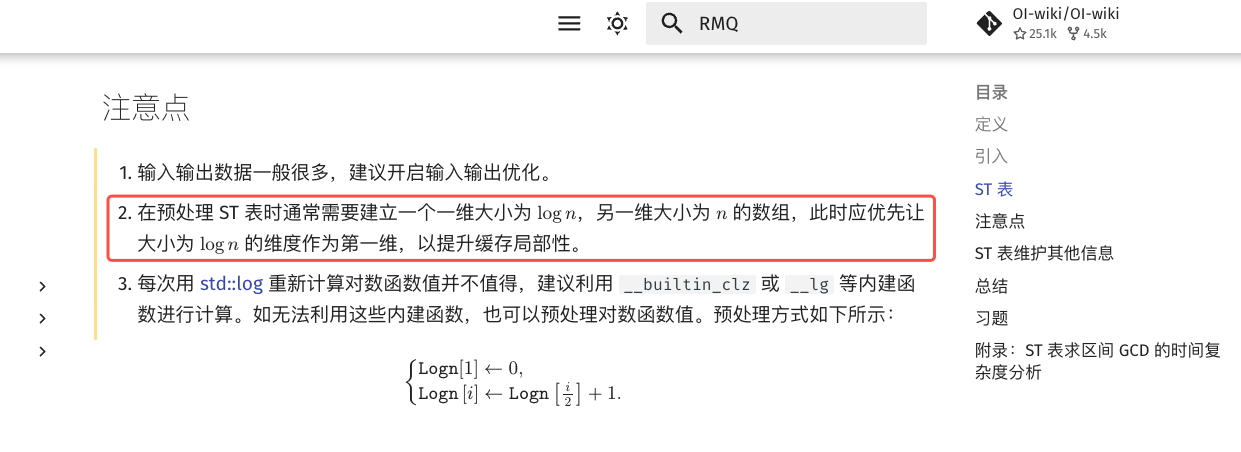
于是我按照这个建议调整了 ST 表数组的维度顺序，代码就顺利通过了。

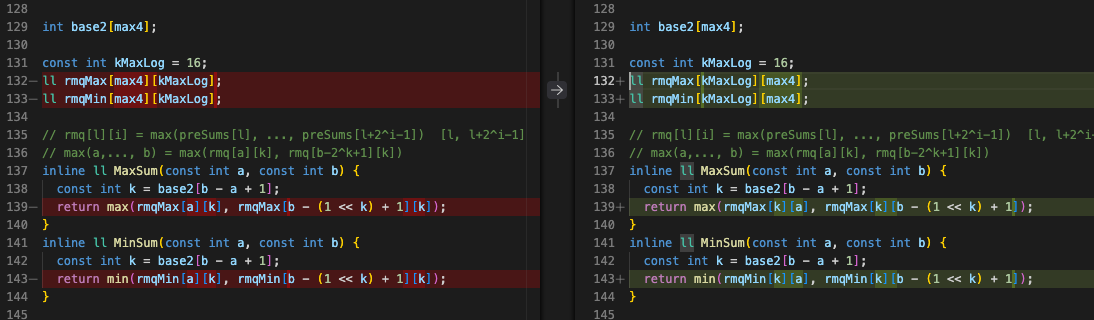
代码也上传到网盘上了。

三、总结

二维数组的定义确实很有讲究，之前从来没被卡住过常数，所以一直没去关心这个顺序。
看来，以后还是需要始终注意这一点：小基数在高维，大基数在低维，从而可以利用局部性原理，提高效率。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code