数据结构详解: ST 表 - 区间最值/GCD/LCM 运算
作者: | 更新日期:
Sparse Table 是什么?都能解决哪些问题?
本文首发于公众号:天空的代码世界,微信号:tiankonguse
零、背景
在数据结构中,ST 表的全称是 Sparse Table,是一种可以支持静态区间查询的数据结构。
下面我们来看下 ST 表的原理,以及它的一些应用,最后分享下我封装的模板。
一、原理
ST 表本质上属于动态规划。
在查询时,将原区间问题转化为两个已经预处理计算过的区间子问题,从而做到 O(1) 的查询。
如下图,询问的是 [L,R] 区间问题,但是我们可以找到一个长度 A,使得 [L,R] 区间问题可以转化为 [L,L+A-1] 和 [R-A+1,R] 两个区间问题,然后再根据子问题的答案合并出原问题的答案。
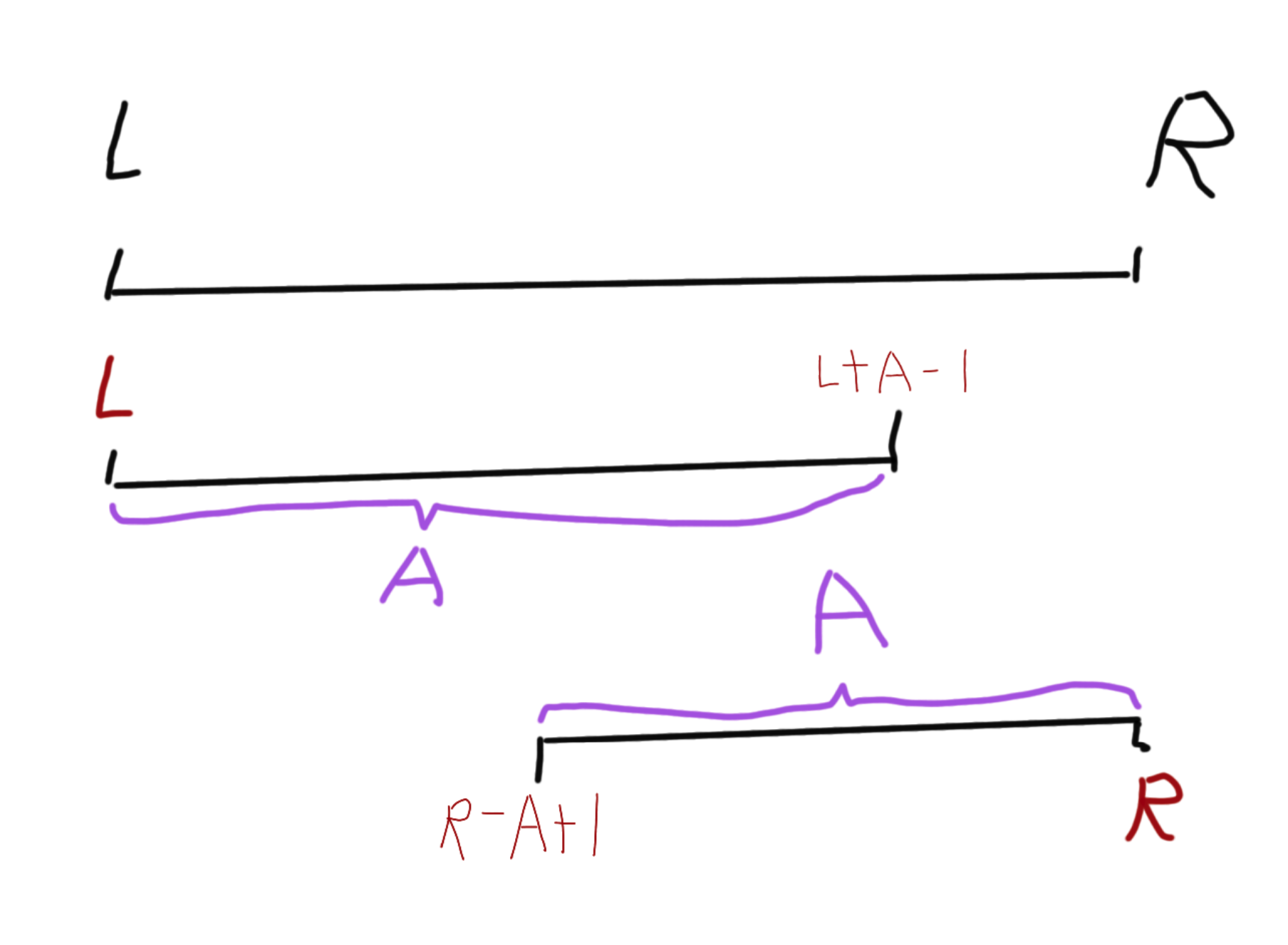
在 ST 表中,这个 A 是一个不大于区间长度 [R-L+1] 的幂次方,即 A = 2^k,k 是一个不大于 log(R-L+1) 的整数。
子问题的计算也一样,通过递归的方法来解决。

那这些离线计算好的子问题该怎么存呢?
如果直接存 st[i][A],空间复杂度就是 O(n^2) 了。
但是可以发现,由于子问题的长度是正数幂,个数最多只有 log(n) 个,所以对于 A=2^k,可以使用 k 来代替 A。
这样就存成 st[i][k],空间复杂度就是 O(nlogn)。
这样,我们就理解了 ST 表的基本原理。
二、应用 - 幂等性
根据 ST 表的原理,我们可以解决很多问题。
例如,区间最大值、区间最小值。
inline ll QueryMax(const int a, const int b) {
const int k = lg2(b - a + 1);
return max(stMax[k][a], stMax[k][b - (1 << k) + 1]);
}
inline ll QueryMin(const int a, const int b) {
const int k = lg2(b - a + 1);
return min(stMin[k][a], stMin[k][b - (1 << k) + 1]);
}
可以发现,拆分子问题的时候,区间是有重叠的。
为何区间有重叠,存在重复计算还能得到正确答案呢?
在数学上,允许重复运算的性质叫做幂等。
即对于合并函数,max(a, a) = a。
基于这个幂等性质,我们可以找到很多应用场景。
1)区间最大值
2)区间最小值
3)区间 GCD(最大公约数)
4)区间 LCM(最小公倍数)
5)区间按位或
6)区间按位与
下面封装了一个简单的模板,应用时,只需要把合并函数进行替换即可。
typedef long long ll;
const int max4 = 50010;
// 使用内建函数计算 ⌊ log_2 x ⌋
inline int lg2(int x) { return 31 - __builtin_clz(x); } // 内建函数,O(1)
// inline int Lg(int x) { return __lg(x); } // 内建函数,O(1), mac 不支持
inline int Log(int x) { return Log2(x); }
const int kMaxLog = 16;
ll stMax[kMaxLog][max4];
inline ll Max(const ll a, const ll b) { return a > b ? a : b; }
inline ll QueryMax(const int a, const int b) {
const int k = lg2(b - a + 1);
ll left = stMax[k][a];
ll right = stMax[k][b - (1 << k) + 1];
return Max(left, right);
}
void InitSparseTable(int n, ll nums[]) {
int maxLog = Log(n) + 1;
stMax[0][0] = 0;
for (int i = 1; i <= n; i++) {
stMax[0][i] = nums[i]; // [1...n]
}
for (int k = 1; k < maxLog; k++) {
for (int i = 0; i + (1 << k) - 1 <= n; i++) {
stMax[k][i] = Max(stMax[k - 1][i], stMax[k - 1][i + (1 << (k - 1))]);
}
}
}
三、应用 - 结合律
很多人会有疑问,区间和是否可以使用 ST 表来查询呢?
答案是肯定的。
不过,这时候子问题就需要重新定义了,即子问题不能有重叠。
这里抽象一下,就是对于一个区间长度,需要把它表示成若干个 2 的幂之和,而且这些幂对应的区间不能重叠。
这不就是经典的二进制表示吗?
inline ll QuerySum(const int a, const int b) {
int K = b - a + 1;
int o = a;
ll ret = 0;
for (int k = 0; K; k++) {
if (K & 1) {
ret += stSum[k][o];
o += 1 << k;
}
K >>= 1;
}
return ret;
}
既然区间和可以使用 ST 表来解决,那还有哪些区间问题可以使用 ST 表来解决呢?
数学上抽象总结下,只要满足结合律的运算,都可以使用 ST 表来解决。
结合律就是通过任意地加括号调整运算顺序,都不影响答案。
例如 a op (b op c) = (a op b) op c。
满足结合律的有:
1)区间和
2)区间异或
3)区间乘积
只利用结合律来计算,复杂度是 O(log(n))。
其实,这些用前缀和(或前缀异或、前缀积)来查询,复杂度更低,是 O(1) 的。
但是需要满足前缀和的差运算,对应乘积就是逆元运算了
不过这里还是介绍下这个方法,当前缀和无法解决的时候,就可以考虑使用 ST 表。
考虑到不同的结合律初始值不一样,例如乘法初始值是 1,加法初始值是 0。
模板的区间查询时,先获取区间的第一个值,然后对剩余的区间进行二进制展开。
typedef long long ll;
const int max4 = 50010;
// 使用内建函数计算 ⌊ log_2 x ⌋
inline int lg2(int x) { return 31 - __builtin_clz(x); } // 内建函数,O(1)
// inline int Lg(int x) { return __lg(x); } // 内建函数,O(1)
inline int Log(int x) { return Log2(x); }
const int kMaxLog = 16;
ll stSum[kMaxLog][max4];
inline ll Sum(const ll a, const ll b) { return a + b; }
inline ll QuerySum(const int a, const int b) {
int K = b - a + 1;
if ((K & (K - 1)) == 0) { // K 是 2 的幂
const int k = lg2(K);
return stSum[k][a];
} else {
int o = a;
ll ret = stSum[0][o];
K--, o++;
for (int k = 0; K; k++) {
if (K & 1) {
ret = Sum(ret, stSum[k][o]);
o += 1 << k;
}
K >>= 1;
}
return ret;
}
}
void InitSparseTable(int n, ll nums[]) {
int maxLog = Log(n) + 1;
stSum[0][0] = 0;
for (int i = 1; i <= n; i++) {
stSum[0][i] = nums[i]; // [1...n]
}
for (int k = 1; k < maxLog; k++) {
for (int i = 0; i + (1 << k) - 1 <= n; i++) {
stSum[k][i] = Sum(stSum[k - 1][i], stSum[k - 1][i + (1 << (k - 1))]);
}
}
}
四、最后
写 ST 表有两个注意事项。
第一,ST 表的二维数组第一维需要是 2 的幂,第二维是区间长度,例如 st[K][N]。
简单理解就是,个数小的在前面,个数大的在后面,这样性能更高。
第二,在获取不大于 n 的最大的 2 的幂时,最好使用内建函数,或者自己预处理计算好。
直接使用数学库里的 log 来算,复杂度就是 O(log n) 了。
而使用 31 - __builtin_clz(x) 或者 __lg(x),复杂度是 O(1)。
如果不想用内建函数,也可以自己打表实现一个 Log2 函数。
const int max4 = 50010;
int base2[max4];
void InitBase2(int n) {
base2[1] = 0;
for (int i = 2; i <= n; i++) {
base2[i] = base2[i >> 1] + 1;
}
}
inline int Log2(int x) { return base2[x]; }
好了,ST 表就讲到这里,希望对你有帮助。
《完》
-EOF-
本文公众号:天空的代码世界
个人微信号:tiankonguse
公众号 ID:tiankonguse-code
本文首发于公众号:天空的代码世界,微信号:tiankonguse
如果你想留言,可以在微信里面关注公众号进行留言。
