NOIP 1997 提高组算法题解 - 启发式搜索

零、背景

1997 年举办的 NOIP 算法比赛中，普及组和提高组各只有一道题目。
在此前的文章《NOIP 1997 普及组算法题解》中，我已经分享过普及组的题解。
本文将分享提高组的题解与解题思路。

PS：题解代码已上传至网盘，公众号回复 NOIP-1997-S 可获取。

一、棋盘问题

题目：给定一个 N×N 的棋盘，将数字 1~N*N 填入棋盘，使得任意两个相邻的数字之和为质数。
若存在多种解，则输出使第一行与第一列之和最小的排列方案。
若无解，则输出 NO。

二、暴力搜索

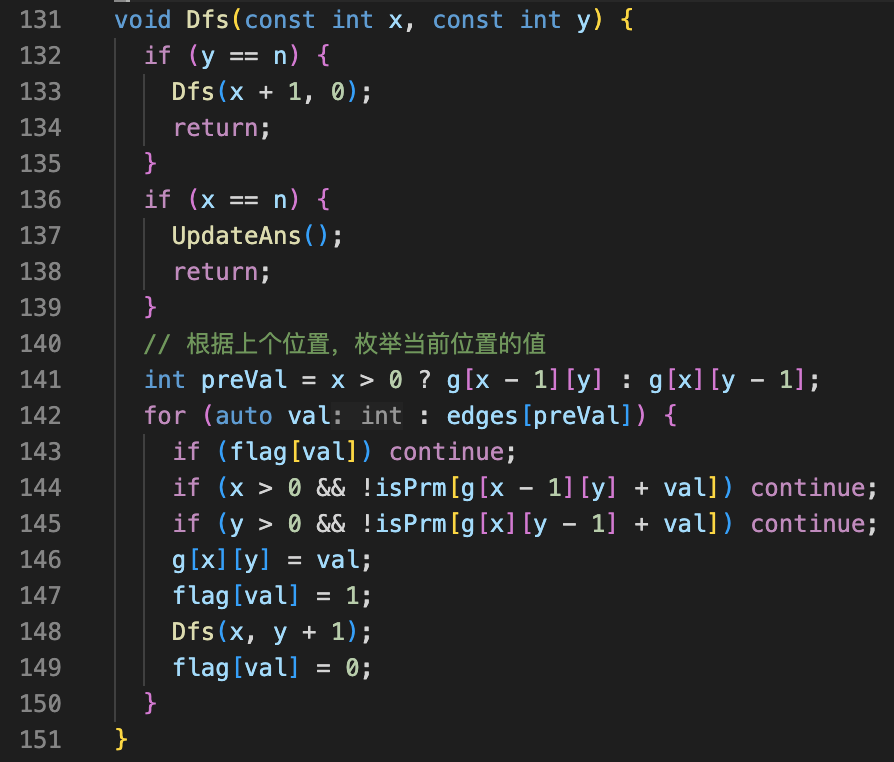
由于条件是相邻数字之和为质数，因此可以预处理出在 1~N*N 范围内每个数字能与哪些数字配对使和为质数。
在搜索时，按行逐个位置枚举可填的数字，并判断该选择是否与已填位置冲突，直至所有位置填满并更新最优答案。
复杂度近似为 O((N*N)!)，但素数约束会显著减少搜索空间。

对于 N 最大为 5 的情况，未经过多优化即可得满分。
对于 N 最大为 10 的情况，单纯暴力搜索通常只能得 50 分左右。

三、优先枚举策略

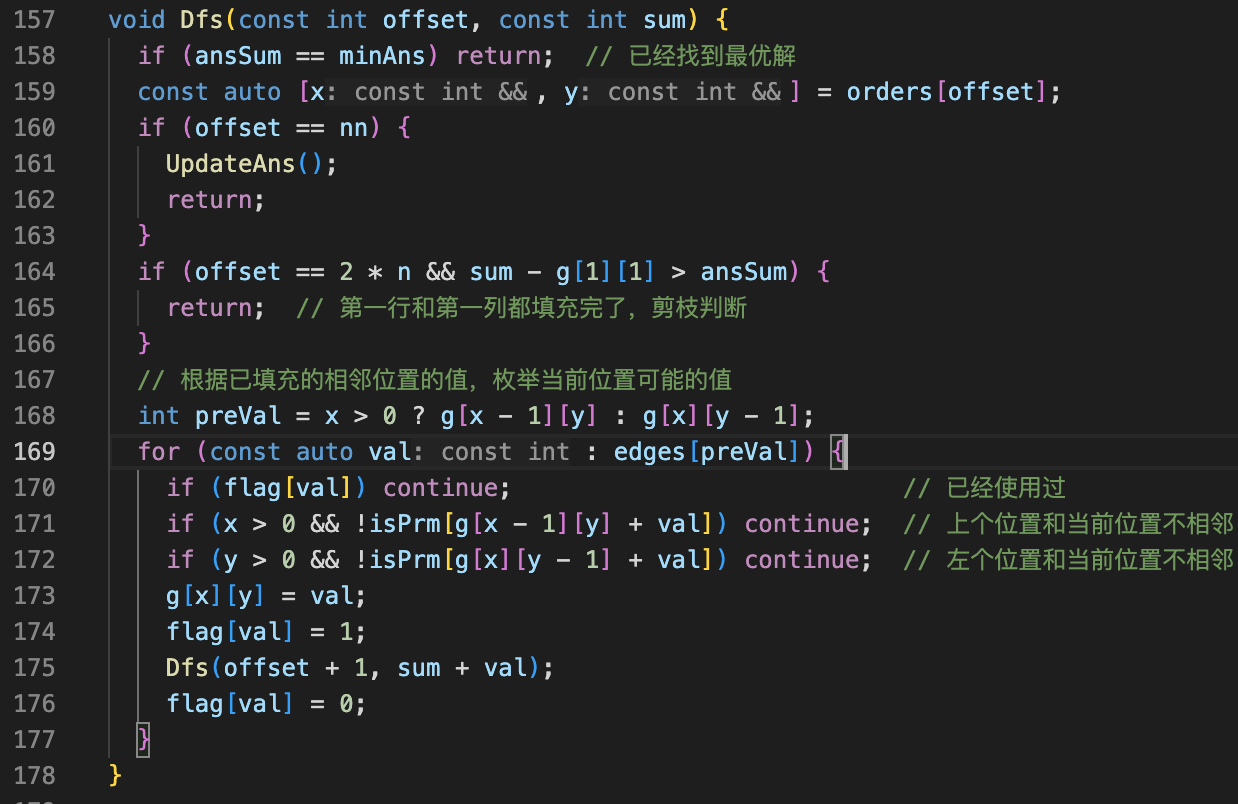
由于题目要求在多解时选择第一行与第一列之和最小的方案，搜索时可以优先枚举第一行与第一列的排列并计算其和，用于后续剪枝。
这种优先枚举可以显著缩小搜索空间，并提升找到较优解的概率。
该策略能将得分提高到约 60 分。

四、迭代加深策略

优先枚举策略需要先找到一个可行解作为上界，然后才能用该上界进行剪枝。
若初始找到的解代价较大，剪枝效果将受限。

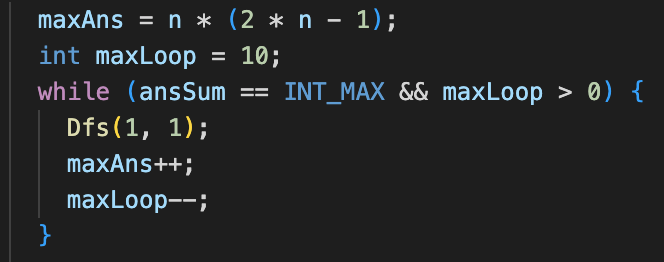
因此可以采用从小到大的迭代加深策略，按目标和的上限逐步搜索可行解。
一旦在某一层找到可行解，即可断定该解为最优解并停止搜索。
该策略可将得分提升到约 90 分。

五、元素的上限策略

通过分析已知可行解可以发现，当 N 为奇数时，仅使用连续数字 1~2*N-1 常常就能构造出可行排列。
当 N 为偶数时，使用连续数字 1~2*N 则更常见。
因此在搜索时可以先尝试较小的数字集（例如优先枚举 1~2*N-1），若无解再扩展到 1~2*N，以减少枚举规模。

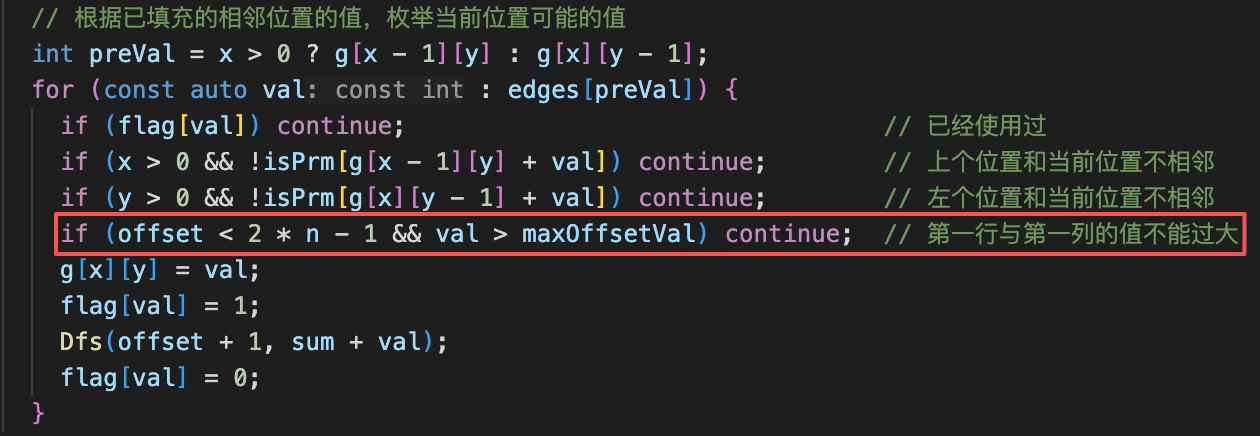
得分：100 分。

六、打表

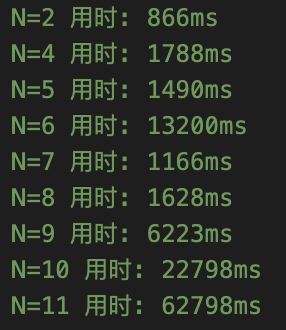
即便采用多种优化手段，当 N 的上界较大（如 N=10）时，仍可能需要较长时间完成搜索。
因此可以在本地预先把各个 N 的最优解计算并保存为表格，比赛时直接查表输出，从而节省比赛中的计算时间。

七、最后

本题在赛题中只考察到 N=5 的情况，对于该规模不做复杂优化也能在合理时间内枚举完所有解。
但若把 N 扩充到 10，则需要结合多种优化策略才能在可接受的时间内得到结果。

具体的优化需要依据题目特点进行设计与组合。
例如当目标是最小化第一行与第一列之和时，可优先枚举这两部分以便有效剪枝。
再例如当约束是“相邻数字之和为素数”时，应当预处理每个数字可配对的数字集合以便快速判断合法性。

希望这篇题解对大家有所帮助。

《完》

-EOF-

本文公众号：天空的代码世界

个人微信号：tiankonguse

公众号ID：tiankonguse-code