NOI 1997 day1 算法题解

零、背景

1997 年举办的 NOIP 算法比赛中，《普及组》和《提高组》题解都分享过了。

这篇文章来分享下 1997 年 NOI day1 的算法题解。

PS：题解代码已上传至网盘，公众号回复 NOI-1997 可获取。

一、竞赛排名

题意：N 个人参加 8 门竞赛，第 i 个人在第 j 门的成绩记为 x[i][j]。
第 j 门的平均分记为 avg[j] = (sum_{i=0..N} x[i][j]) / N。
每个人的总分记为 sumsX[i] = sum_{j=1..8} x[i][j]。
第 j 门的偏差分记为 dis[j] = (sum_{i=0..N} |x[i][j] - avg[j]|) / N。
每个人在第 j 门的“位置分”定义为 y[i][j] = (x[i][j] - avg[j]) / dis[j]（若 dis[j] 为 0，值为 0）。
选手的总位置分记为 sumY[i] = sum_{j=0..3} y[i][j] + 0.8 * sum_{j=4..7} y[i][j]。

排名规则如下：
优先按总位置分从高到低排序。
如果总位置分相同，则按总分从高到低排序。
如果总分相同，则按编号从低到高排序。

求每个学生的排名。

思路：按题意计算每个定义的分数，然后进行排序即可。

由于怕存在精度问题，我自己封装了一个分数类，通过分数类进行四则运算。

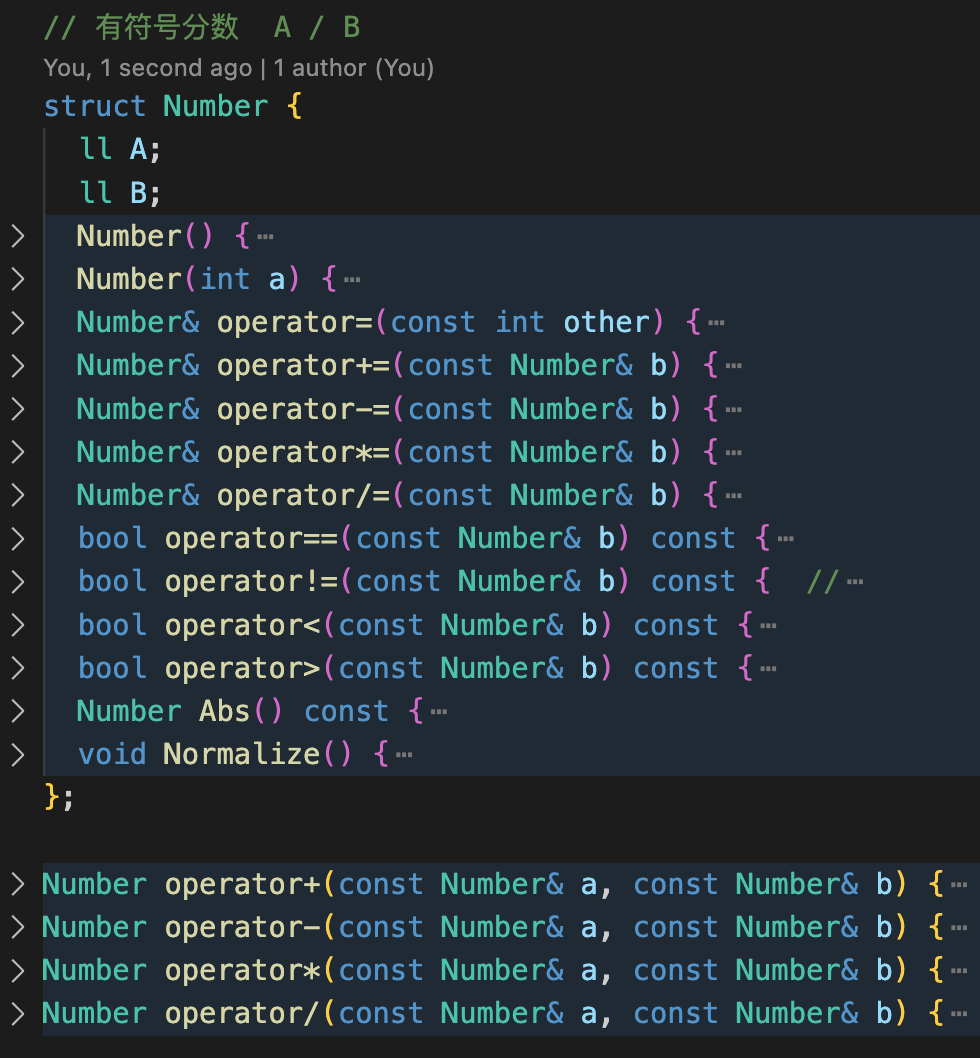
得分：0 分。
原因：使用分数类表示时，avg 和 dis 的分母在多次运算或累加过程中可能会增长得很快，中间整数会超过整型上限，导致结果错误。

后来改为使用 double 计算后，能通过更多测试。
得分：80 分。
原因：原先使用的 eps = 1e-7 在比较时不够严格。

解决方法1：将 eps 定义为 1e-10。
解决方法2：对 sumY 做统一放大（例如 N*N），可以把 avg[j] 和 dis[j] 中的分母约掉，转为整数形式来计算，从而减少浮点误差。
得分： 100 分。

二、积木游戏

题意：给 N 个有编号的立方体积木，并告诉你立方体的三个边长。
现在需要从 N 个立方体中选择若干立方体，分成 M 组。
且每组至少 1 个立方体，且第 k 组的所有立方体编号都需要小于第 k+1 组的所有立方体编号。

另外，对于每组的立方体需要从下到上摞起来，要求下面立方体的接触面能够完全覆盖上面立方体的接触面。
另外还要求下面的立方体的编号要小于上面的立方体编号。

求如何选择，才能使得 M 组立方体的高度和最大。

洛谷的错误题目：洛谷上在介绍第 k 组与第 k+1组的关系时，特别强调 k 最小是 2。

这意味着第一组是不需要满足这个条件的。
我基于这个写了一个很复杂的动态规划，但是样例无法通过。
最后看了题解，发现 k 最小是 1。

回到题目本身，需要先理解题意。
其中需要明白，并不是所有立方体都需要被选择。
因为题目说的是选择若干立方体。

题意确定后，按题意设计状态即可。

状态1：dp[r][k] 前 r 个立方体，选择组成 K 组的最大高度。

针对最后一个元素，分为选择与不选择两种情况。
不选择，答案就是 dp[r-1][k]。
选择时，说明最后一个元素属于第 k 组。

此时，第 r 个立方体作为第 k 组最上面的立方体，需要枚举确定使用哪个接触面。
另外，还需要枚举确定第 k 组的区间大小。

这两个确定了，就得到了第二个状态：dp[l][r][s] 第 l 到 r 个立方体，且第 r 个立方体必须选择使用 s 面，可以得到的最大高度。

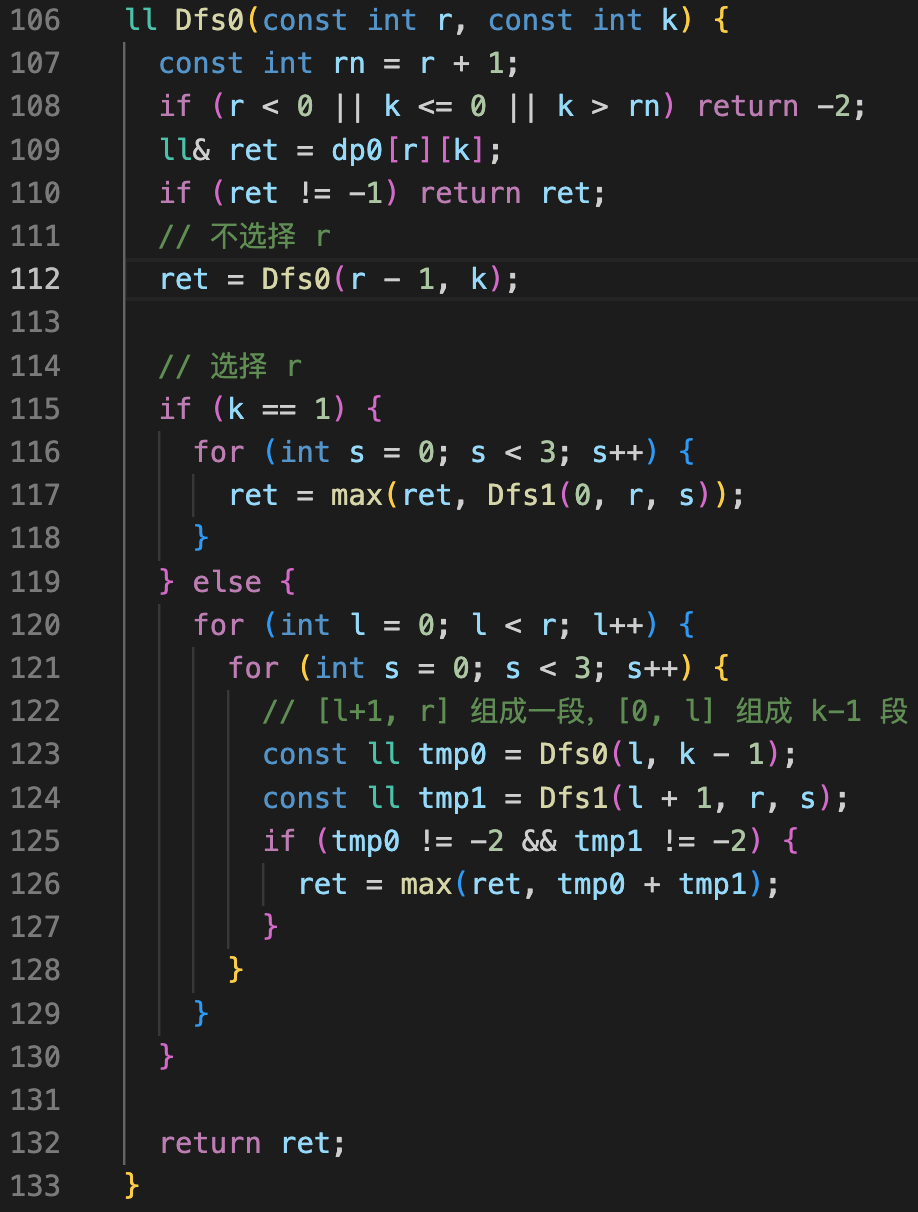
对于第二个状态，就是一个典型的区间 DP。
这里枚举下个选择的立方体的位置，即可递归计算。

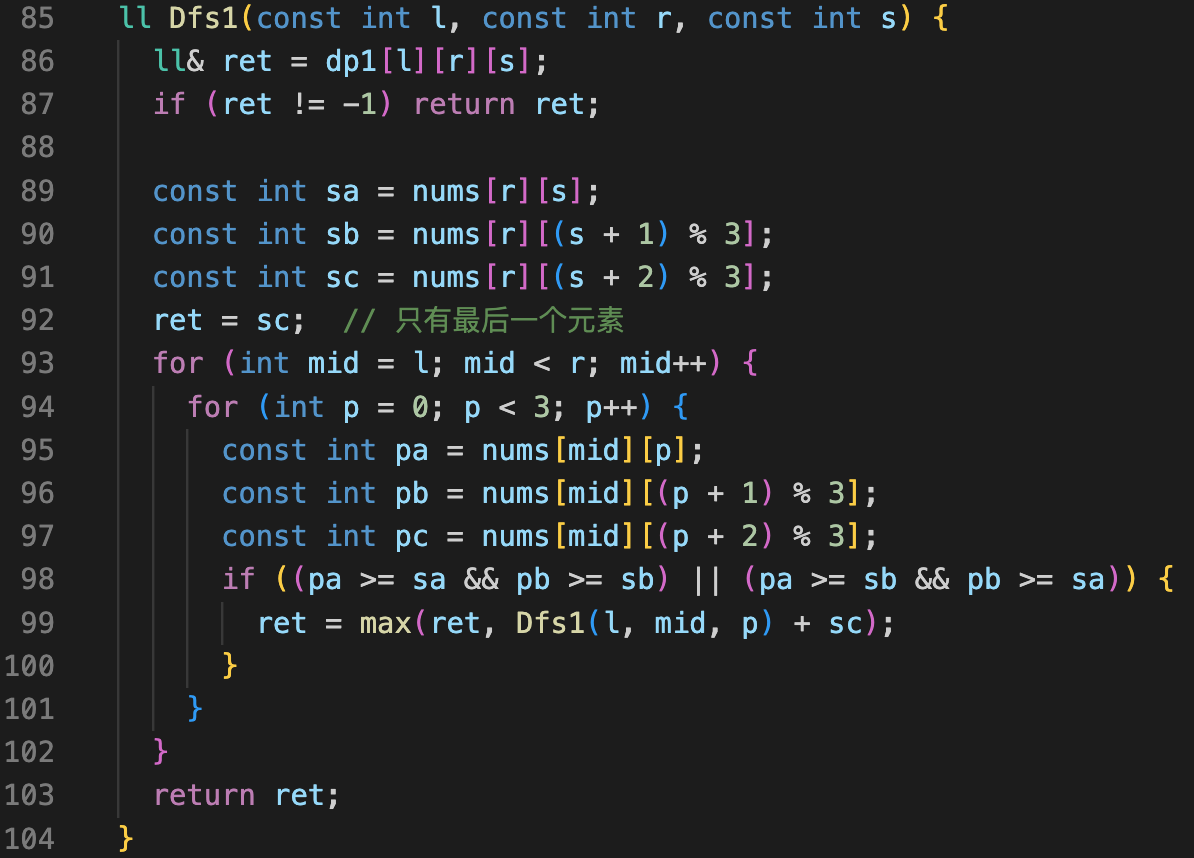
复杂度：O(n^3)
得分：100 分。

当然，这个也可以只定义一个状态转移方程 dp[r][m][s] 代表前 r 个元素，选择组成 m 组，且最后一个属于第 m 组的最大高度和。
这个本质上是把两个状态合并成一个状态，是等价的。

三、最佳游览

题意：给一个网格，求选择一个左右区间，区间内每一列选择一个元素，使得选择的元素和最大。

注：原始题意不好介绍，这里进行了简化。

思路：线性DP。

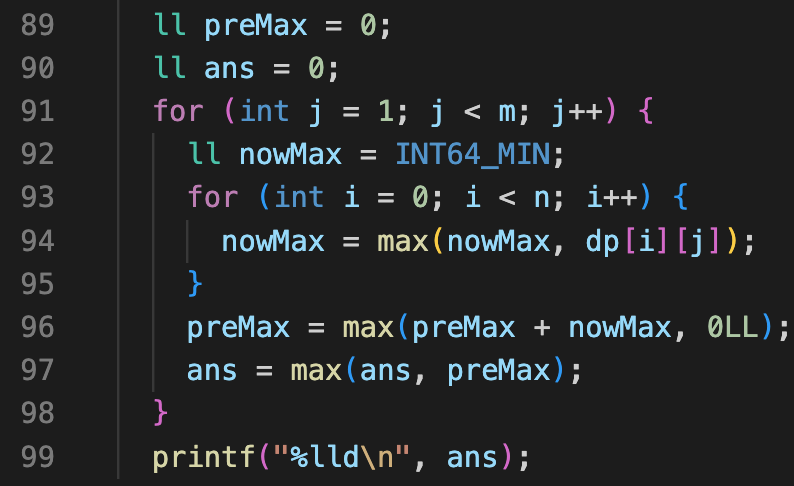
记录一个最大的后缀和，如果为负时，设置为 0。
然后每一列选择最大的元素，更新最大后缀和即可。
等价于最大连续子数组和问题。

四、最后

NOI 1997 第一天的比赛还是比较简单的。
第一题为模拟题，使用整数分数会有精度问题。
第二题是多维 DP，数据规模不大，按题意添加所需状态即可。
第三题则是最大连续子数组和问题。

好的，NOI 1997 第一天的比赛就到这里了。

《完》

-EOF-

本文公众号：天空的代码世界

个人微信号：tiankonguse

公众号ID：tiankonguse-code