leetcode 第 366 场算法比赛

零、背景

这次比赛题目比较简单，不过由于国庆调休加班，我没参加比赛。

leetcode 仓库地址：https://github.com/tiankonguse/leetcode-solutions

比赛代码：contest/3/366

一、分类求和并作差

题意：给两个整数 n 和 m，问整数范围 [1,n] 之内，不能被 m 整除的数字之和 num1 与 可以整除的数字之和 num2 的差num1-num2。

思路1：枚举计算。
按题意循环计算出两个和，求差。
复杂度: O(n)

思路2：公式计算。

能够被整除的数字是确定的，即m,2m,...,n/m*m
所以能够被除的数字之和 num2 为 m * sum(1, n/m)。

无法整除的数字之和为所有数字的和减去能够整除的数字之和。
所以，无法整除的数字之和 num1 为 sum(1,n) - num2。

由此，可以计算出答案。
复杂度: O(1)

二、最小处理时间

题意：有 n 个处理器，每个处理器有4个核，启动需要预热一段时间。
现在有4n个任务，每个核只执行一个任务，问所有任务执行完的最小时间。

思路：由于每个核只执行一个任务，则每个任务的完成时间为p[i] + t[i]。
显然，对于耗时较长的任务，需要分配预热时间较短的核心。
所以对核正序排序，任务倒序排序，然后按顺序匹配即可。

思考题：每个核可以运行任意个任务，该怎么做呢？

三、执行操作使两个字符串相等

题意：给两个长度相等的二进制以及一个代价 x。
现在可以对第一个字符串进行任意次操作。
操作1：任意选择两个下标，二进制进行翻转，代价为 x。
操作2：选择相邻的两个下标，二进制进行翻转，代价为 1。
问把第一个二进制转换为第二个二进制的最小代价是多少，如果不可以转换，输出-1.

思路：动态规划。

首先判断是否有答案。
每次操作两个位置的值进行翻转，则操作n次后是 2n个位置的值翻转。
如果两个二进制值不一样的位置个数是偶数，则肯定存在答案，否则不存在答案。

首先我们可以证明，对于相等的前缀，不做操作是最优的。

之后，看第一个值不相等的下标，可以发现，这个位置要么选择一次操作1，要么选择1次操作2。
不可能不选择，操作多次不可能有更优解。

如果选择操作1，意味着后面某个位置被选中，是谁我们不知道，记为预留下标。
如果选择操作2，意味着下个位置被选中，下个位置的值需要翻转。

由此，我们可以定义状态f(i, flag, left)。
含义是从第 i 个下标开始的最优答案，flag 代表当前下标是否需要翻转，left 代表预留下标的个数。

如果当前下标与 flag 计算后，值是相等的，则不需要操作，答案为 f(i+1, 0, left)。
如果当前下标与 flag 计算后，值不相等的，则需要进行操作。

操作分为三种情况。
情况1：预留下标大于0，使用预留下标，没有代价。
情况2：进行操作1,代价为 x + Dfs(p + 1, 0, left + 1)。
情况3：进行操作2，代价为 1 + Dfs(p + 1, 1, left)。

由此，可以计算出答案。
复杂度：O(n^2)

优化：

分析可以发现，对于操作2，肯定是连续操作的，目的是使得某两个不同位置进行翻转。
即如下：

10001
01001
00101
00011
00000

进而可以推论出，对于连续的操作2，肯定是对相邻的不同位置进行翻转，选择了操作2的位置不可能选择操作1。

进而可以推论出，最优答案是对不同位置进行划分，一类划分是相邻的不同位置，进行操作2，其他不同的位置随机匹配进行操作1。

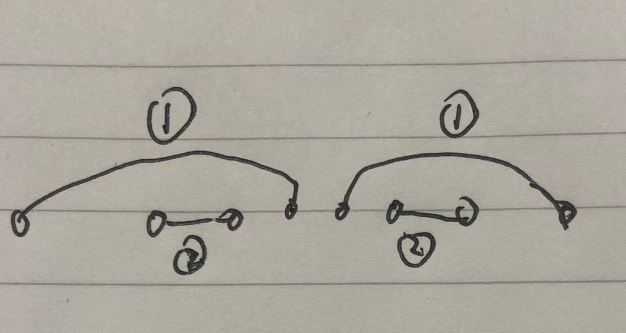
如果提前对所有不同位置分配操作1，则每个位置的代价为 x/2。
我们挑选相邻两个不同位置进行操作2，则可能使得答案更优。

定义状态：f(i) 前 i 个不同位置当前的最优答案。

对于第 i 个不同位置，有两个选择。
选择1：随机选择不同的位置进行匹配，则答案为 f(i-1) + x/2。
选择2：与前一个不同位置匹配进行操作2，则答案是 f(i-2) + 1。

复杂度：O(n)

四、对数组执行操作使平方和最大

题意：给一个数组和k，对数组进行任意次操作，最后选择 k 个元素，求这 k 个元素的最大平方和。
操作：任意选择两个位置i,j，第一个位置值为V[i]&V[j],第二个位置值为V[i]|V[j]。

思路：贪心。

操作的含义是将两个数字的二进制不同项进行转移。
假设两个值为a,b，不同项为 a^b，转移后值分别为 a-a^b 和 b+a^b。

对于两个元素，是否需要进行操作，以及如何操作才会得到更大的平方和呢？
假设 a>b，这里也是分三种情况。

ans1=a^2+b^2

ans2=(a-c)^2+(b+c)^2
=a^2-2ac+c^2 + b^2+2ba+c^2
=a^2+b^2 +2c^2 + 2c(b-a)


ans3=(a+c)^2+(b-c)^2
=a^2+2ac+c^2 + b^2-2ba+c^2
=a^2+b^2 +2c^2 + 2c(a-b)

由于b>a，所以ans2>ans3，且 ans2>ans1。
所以，较小的数字把二进制让给较大的数字，答案会更优。

根据上面的结论，可以得出两个结论：
1、未选择的元素，需要尽可能的把二进制转移给选择的元素。
2、选择的 k 个元素里，需要尽可能的把二进制转移给较大的数字。

换言之，这里不关心数字，只关心二进制的个数。

最终结论：统计各位二进制的个数，k 个数依次选择尽可能多的二进制。
复杂度：O(n log(n))

五、最后

这次比赛比较简单，不过国庆调休，做题的人应该比较少吧。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号ID：tiankonguse-code