leetcode 第 450 场算法比赛-64名，LCA

零、背景

这次比赛其实状态不好，因为最近几晚都睡的比较晚。
如果你关注我之前的文章的话，可以发现我在研究本地 AI 生成图片，一方面本地在大量的研究 prompt 来，另一方面在大量的阅读 comfyUI 的文档，一不留神就到半夜三点了。

起床后头晕，浑浑噩噩的打比赛，第三题纠结了10分钟，第四题一看是带权LCA，自己只写过无权 LCA，于是各种魔改，改了半个小时才通过。
没想到竟然排名 64。

A: 签到题
B: 循环节，并查集
C: 搜索
D: 倍增LCA

排名：64
代码地址： https://github.com/tiankonguse/leetcode-solutions/tree/master/contest

一、数位和等于下标的最小下标

题意：给一些数字，求第一个数位和等于下标的位置。
数位和：一个数字10进制各位之和。

思路：遍历计算每个数字的数位和即可。

int sum = 0;
while (v) {
  sum += v % 10;
  v /= 10;
}

二、数位和排序需要的最小交换次数

题意：给 n 个互不相同的数字，要求按数位和进行排序，如果数位和相等则数值排序。
求排序的最少交换次数。

思路：循环节

首先预处理出数位和，排序，计算出每个数字预期的位置。
这样题目就转化为了若干数字排序，求最小交换次数。

如何交换次数才最少呢？

状态1：假设一个数字就在目标位置，则肯定不交换是最优的。
状态2：假设两个数字互相在对方的位置，则交换一次就可以到达目标位置。
状态3：假设三个数字互相在对方的位置，一次交换最多有一个数字变成在自己的位置，然后就变成了状态2。
状态n: 假设 n 个数字互相在对方的位置（一个循环节），一次交换最多有一个数字变成在自己的位置，然后就变成了状态n-1。

总结：交换次数与循环节大小与个数有关。

答案1：数组个数减去循环节个数。
答案2：所有循环节大小减一后求和。

可以证明，上面两个答案是等价的。

对于答案1，可以使用并查集计算循环节的个数。
对于答案2，则可以不断的按循环节交换，边交换边计算答案。

for (int i = 0; i < n; i++) {
  if (indexs[i] != i) {
    ans++;
    swap(indexs[i], indexs[indexs[i]]);
    i--;
  }
}

三、网格传送门旅游

题意：给一个网格，可以上下左右走，有障碍物，从左上角去右下角。
传送门：相同字母的位置代表传送门，可以零代价互相传送，但只能传一次。
求最小步长。

思路：搜索

题目中要求传送门只能使用一次，这个会把大部门人卡主。
但是分析 BFS 的搜索过程，可以发现搜索后会标记不再回头走，即BFS 自身已经保证重复到达走过的位置，自然就不会重复传送了。

故忽略只能传送一次的条件，无脑搜索即可。

queue<tuple<int, int, int>> q; // 队列，x, y, step
auto Add = [&](int x, int y, int step) {
  if (x < 0 || x >= n || y < 0 || y >= m || matrix[x][y] == '#') return;
  char oldVal = matrix[x][y];
  if (oldVal == '.') {
    q.push({x, y, step});
    matrix[x][y] = '#';
  } else {
    // 不消耗到达所有相连的位置
    // TODO: 题目不确定第一次到达时是不是必须传送
    for (auto [x, y] : portal[oldVal]) {
      if (matrix[x][y] == '#') continue;
      q.push({x, y, step});
      matrix[x][y] = '#';
    }
  }
};

Add(0, 0, 0);
while (!q.empty()) {
  auto [x, y, step] = q.front();
  q.pop();
  if (x == n - 1 && y == m - 1) return step;
  Add(x + 1, y, step + 1);
  Add(x - 1, y, step + 1);
  Add(x, y + 1, step + 1);
  Add(x, y - 1, step + 1);
}

四、包含给定路径的最小带权子树 II

题意：给一个带权树，求包含三个点的最小子树的权重值。

思路：标准的倍增LCA

如果是两个点，那就是我们学习 LCA 时的标准题目了。
如果是三点，就会发现情况稍微复杂一些，三点的树形接口有很多中组合。

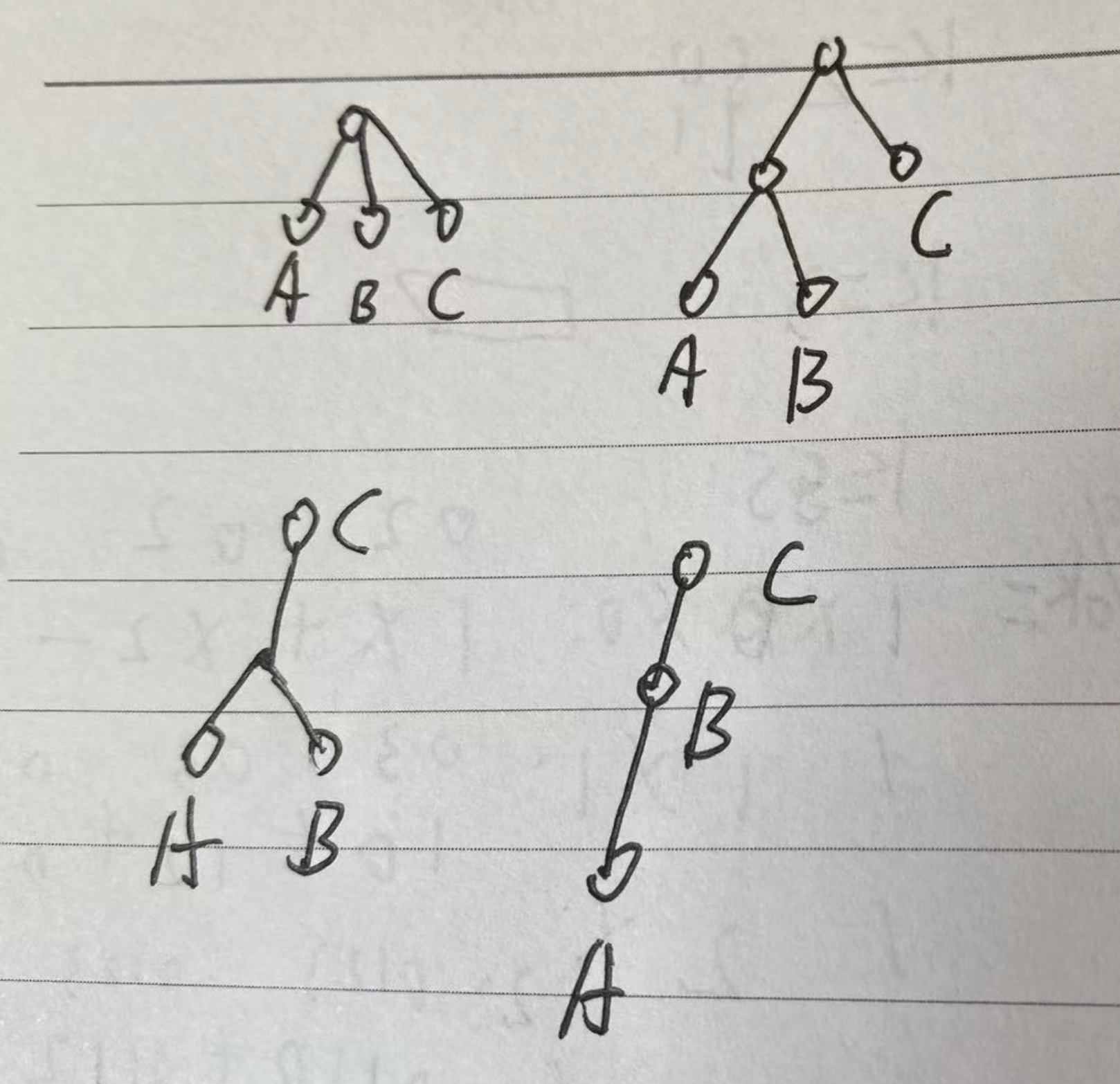
如果再考虑三点自身的排列组合，情况又要翻 6 倍了。

这里假设图形确定了，即 BC 先遇到公共祖先，然后与 A 遇到公共祖先，如下图。
该怎么做这道题呢？

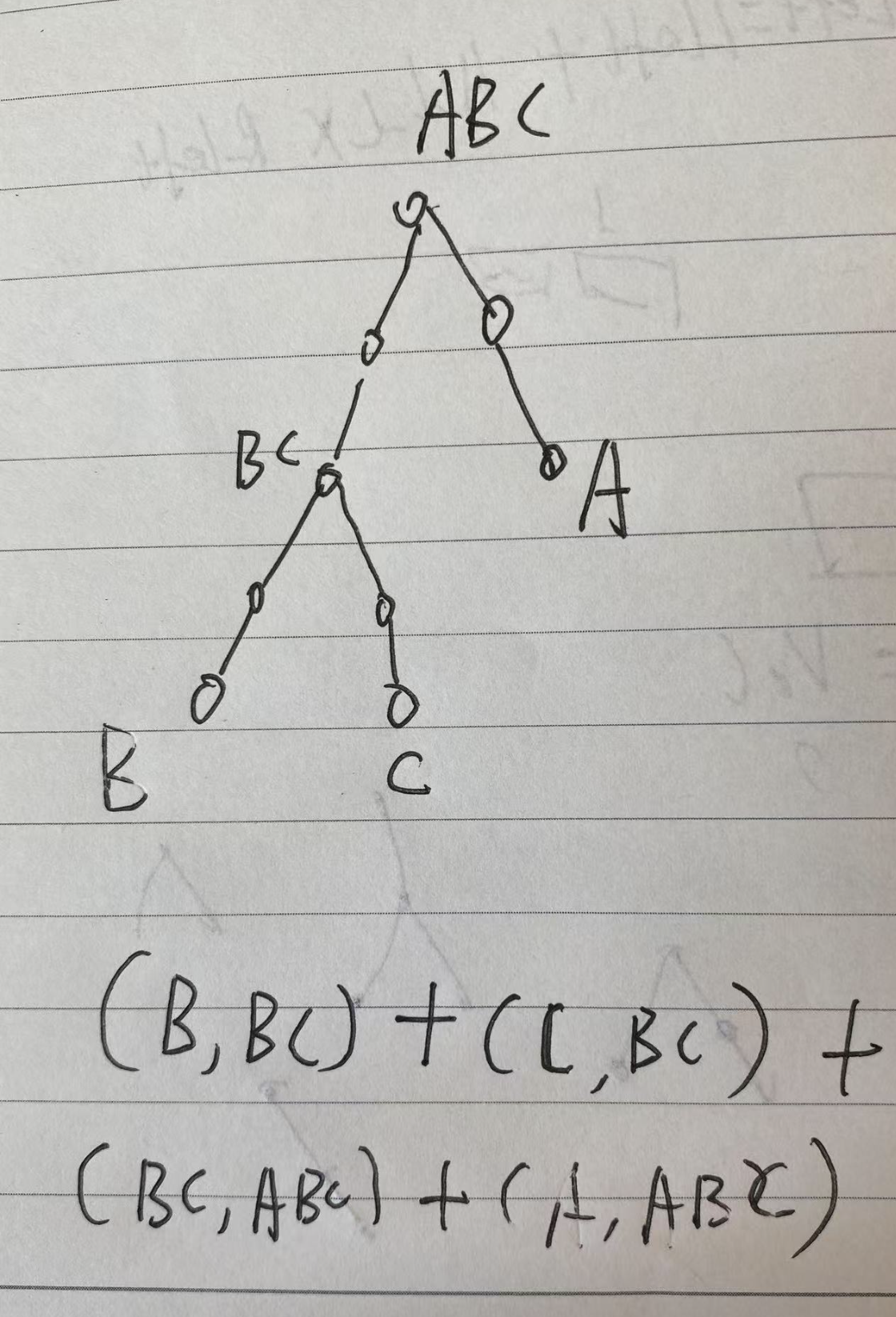
很显然。答案可以按公共祖先把树分成若干线段，然后求出线段的权重和即可。

那怎么找到哪两个点是 B 与 C，哪个点是 A 呢？
本来我要暴力写 if else 的，后来发现可以枚举所有情况，排序。

vector<tuple<int, int, int, int>> nums;
int u0 = q[0], u1 = q[1], u2 = q[2];
nums.push_back({Lca(u0, u1), u0, u1, u2});
nums.push_back({Lca(u0, u2), u0, u2, u1});
nums.push_back({Lca(u1, u2), u1, u2, u0});

sort(nums.begin(), nums.end(), [&](const tuple<int, int, int, int>& a, const tuple<int, int, int, int>& b) {
  int au = get<0>(a), bu = get<0>(b);
  return dep[au] > dep[bu];
});
u0 = get<1>(nums[0]); 
u1 = get<2>(nums[0]);
u2 = get<3>(nums[0]);

接下来需要思考如何求一个节点到某个祖先节点的权重和。
本来我想使用 LCA 做的，后来发现可以使用前缀和做。

auto Dis = [&](int u, int v) {  //
  return pre[u] - dis[v];
};

int sum = 0;
sum += Dis(u0, u01);
sum += Dis(u1, u01);
sum += Dis(u01, u012);
sum += Dis(u2, u012);
ans.push_back(sum);

就怎样，这道题化繁为简，只需要一个标准的 LCA 与一个前缀和，就可以很轻松地求出答案。

五、最后

这次比赛第三题算是有一个小卡点，第四题三个点情况的树形组合情况比较多，也算是一个卡点吧。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号： tiankonguse
公众号 ID： tiankonguse-code

本文首发于公众号：天空的代码世界，微信号：tiankonguse
如果你想留言，可以在微信里面关注公众号进行留言。