NOIP 2024 第二题「遗失的赋值」题解

零、背景

之前已经分享了历年 CSP-J/S 的比赛题解，现在准备开始整理 NOIP 的题解。

为了避免四道题都放在一篇里导致文章过长，我计划每道题单独写一篇，最后再写一篇总览做一个总结。

NOIP 2024 第一道题「编辑字符串」已经在文章《NOIP 2024 第一题 编辑字符串 题解》中分享过了。

这篇文章来分享第二题「遗失的赋值」的题解。

PS：源码已上传网盘，公众号回复 NOIP-2024 获取。

一、题目

给出 n 个变量，每个变量的取值范围为 [1, v]。

在这 n 个变量之间有 n-1 个二元约束关系：如果第 i 个变量的值为 a，那么第 i+1 个变量的值必须为 b。
当第 i 个变量的值不为 a 时，这条二元约束关系就失效，第 i+1 个变量的值可以任意取。

另外，还有 m 条一元约束关系，即第 j 个变量的值被固定为 d。

现在只告诉你这 m 个一元约束关系，求出可能合法的二元约束关系的个数。
这里的「合法」是指：存在一组给 n 个变量赋值的方式，使得所有一元约束和二元约束都能够同时满足。

二、递推分析

每个变量的取值范围都是 [1, v]，我们可以把所有变量的取值情况抽象成一个 v × n 的网格：
行表示取值 1 ~ v，列表示位置 1 ~ n。

没有一元约束关系

如果暂时不考虑一元约束关系，那么每条二元约束关系都可以独立选择，总方案数是 v^(n-1)。

构造的方法：假设你已经任意确定好了这 n-1 条二元约束关系，我们总是可以选择与 b 无关的值，构造出一组合法的 n 个变量取值。

如下图所示，在二元关系确定后，只要起点和终点都选择与这些二元关系无关的值，只要 v > 1，就一定能构造出合法的 n 个变量取值。

一个一元约束关系在最后

如果只有一个一元约束关系，并且它只约束最后一个变量。

此时可以发现，这个一元约束并不会影响二元约束关系的选法，因此二元约束关系的方案数还是 v^(n-1)。

原因也很容易理解：
由于倒数第二个变量可以任意构造（参考「没有一元约束关系」的情况），我们总是可以避免选择 a，从而使得这条二元约束关系失效，所以可以选择任意一个二元约束关系。

一个一元约束关系在开头

假设第一个变量被一元约束固定为 d0，第一个变量到第二个变量的二元约束关系写成 (a0, b0)。
第一个变量的值确定之后，到第二个变量会分两种情况。

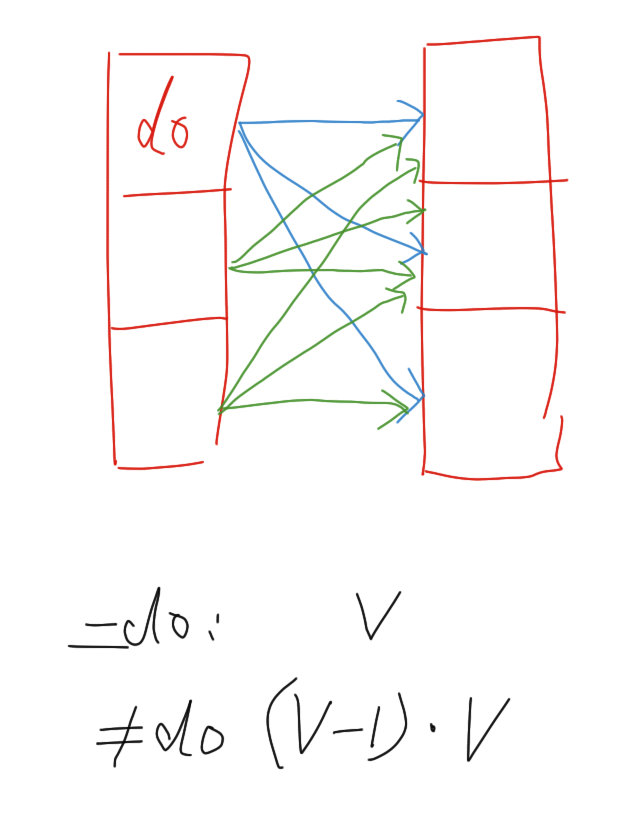
第一种：a0 = d0，此时第二个变量的值只能为 b0。
参考图中的蓝线，从 d0 出发，到下一位一共有 v 种可以选择的 b0，因此共有 v 种二元约束关系满足这种情况。

第二种：a0 != d0，此时第二个变量的值可以为任意值。
参考图中的绿线，不等于 d0 的取值一共有 v-1 个，每个取值出发到达下一位可以任意选择，共有 v 种情况，因此共有 (v-1) * v 种二元约束关系满足这种情况。

从图中还可以发现一个规律：对于不等于 d0 的那 v-1 个取值来说，它们是完全等价的，没有本质区别。

因此，我们在状态转移时，只需要关心「被一元约束固定的取值有多少个」，而不需要关心具体是哪个值被固定。

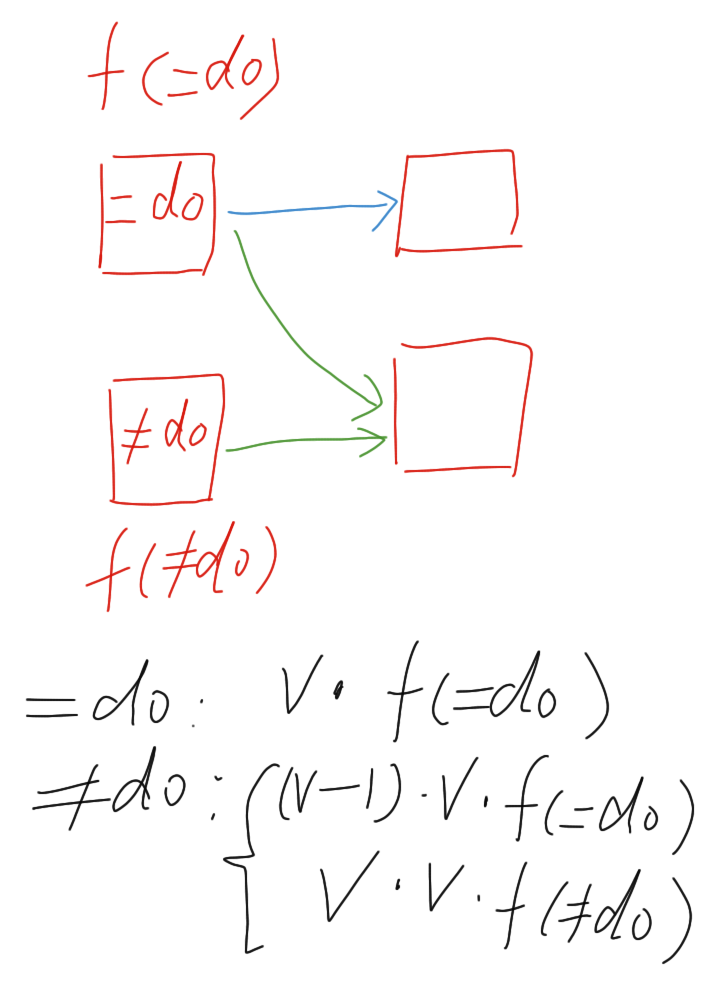
基于这个规律，对于第二个变量，可以总结为：

• 有一元约束的二元关系有 v 个位置；
• 没有一元约束的二元关系有 v * (v-1) 个位置。

每个有约束的二元关系，可以转移到下一个变量的 v 个「有约束」位置，以及 v * (v-1) 个「无约束」位置。
每个无约束的二元关系，可以转移到下一个变量的 v * v 个无约束位置。

假设当前变量有 f(=d0) 个二元关系是被一元约束固定住的，有 f(!d0) 个二元关系是没有被固定的。
如下图，可以推导出在下一位没有一元约束时，这两类二元关系分别转移成多少个新的有约束/无约束方案数。

之后，如果后面都没有一元约束关系，就可以不断按照上面的公式进行迭代，最终计算出所有方案数。

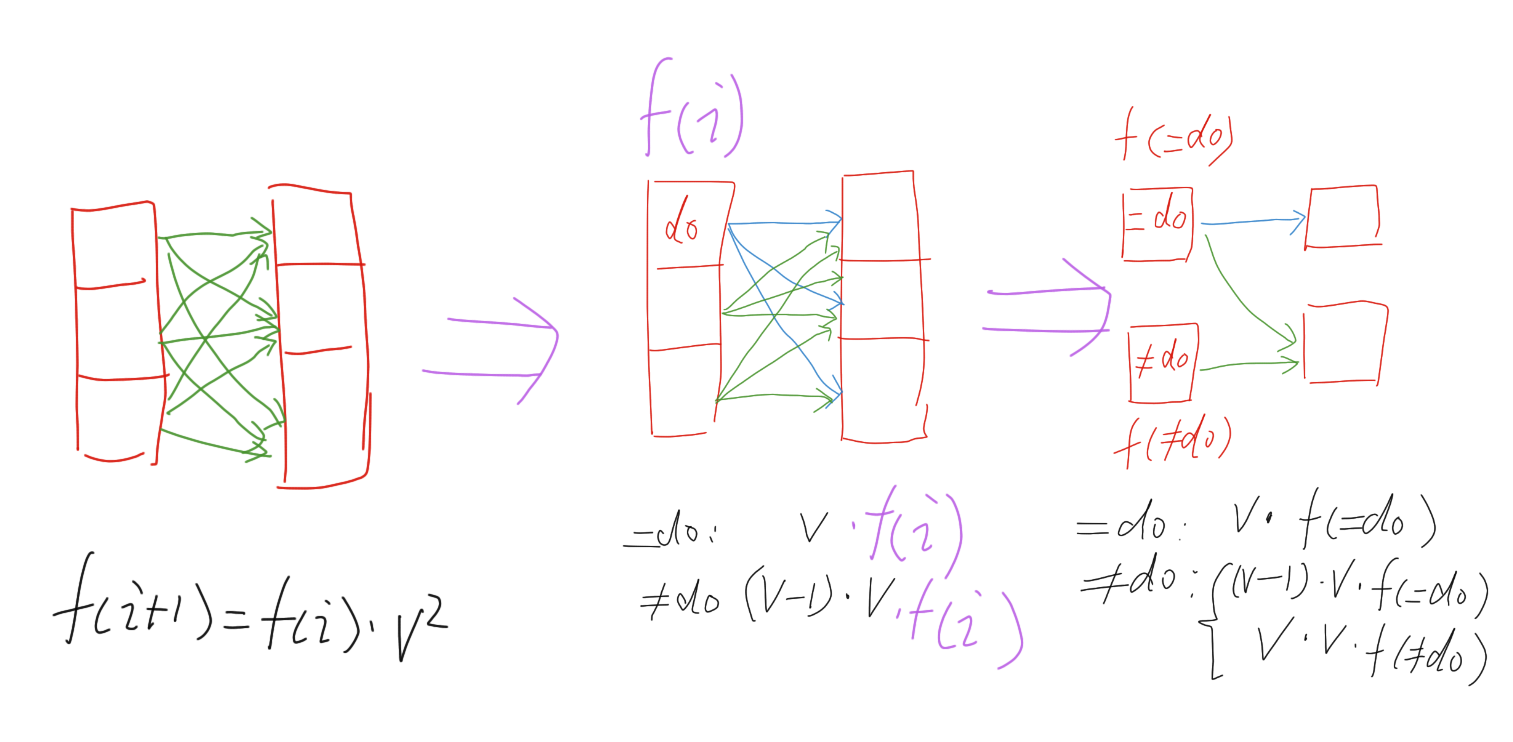
一个一元约束关系在中间

如果一元约束关系在中间某个位置，在真正遇到这一位的一元约束之前，情况与「一元约束在最后」时是完全一样的：
前面这一段不会被后面的那个一元约束影响。

也就是说，如果一元约束关系出现在第 k 个变量上，那么在到达第 k 个变量之前，二元约束关系的方案数仍然是 v^k * v^k 这类形式（前面可以当作「没有一元约束关系」来处理）。

接下来，在遇到这一位的一元约束之后，由于当前变量被固定了取值，出发点固定，与「一个一元约束关系在开头」的情况完全相同，就可以按前面的方式继续推到后面。

多个一元约束关系

多个一元约束关系，可以理解为：在「一个一元约束关系在中间」的基础上，后面又遇到了下一个一元约束 d1。

在遇到下一次一元约束之前，记当前：

• 被一元约束固定住的二元关系数量为 f(=d0)；
• 没有被一元约束固定的二元关系数量为 f(!d0)。

被一元约束固定时，取值是确定的：

• 如果二元关系从 d0 出发，那么到下一位只能走到 d1 这一种取值，共有 f(=d0) 种方案；
• 如果二元关系从 !d0 出发，则下一位可以任意取值，共有 f(=d0) * v * (v-1) 种方案。

没有被一元约束固定时，取值也是任意的，共有 f(!d0) * v * v 种方案。

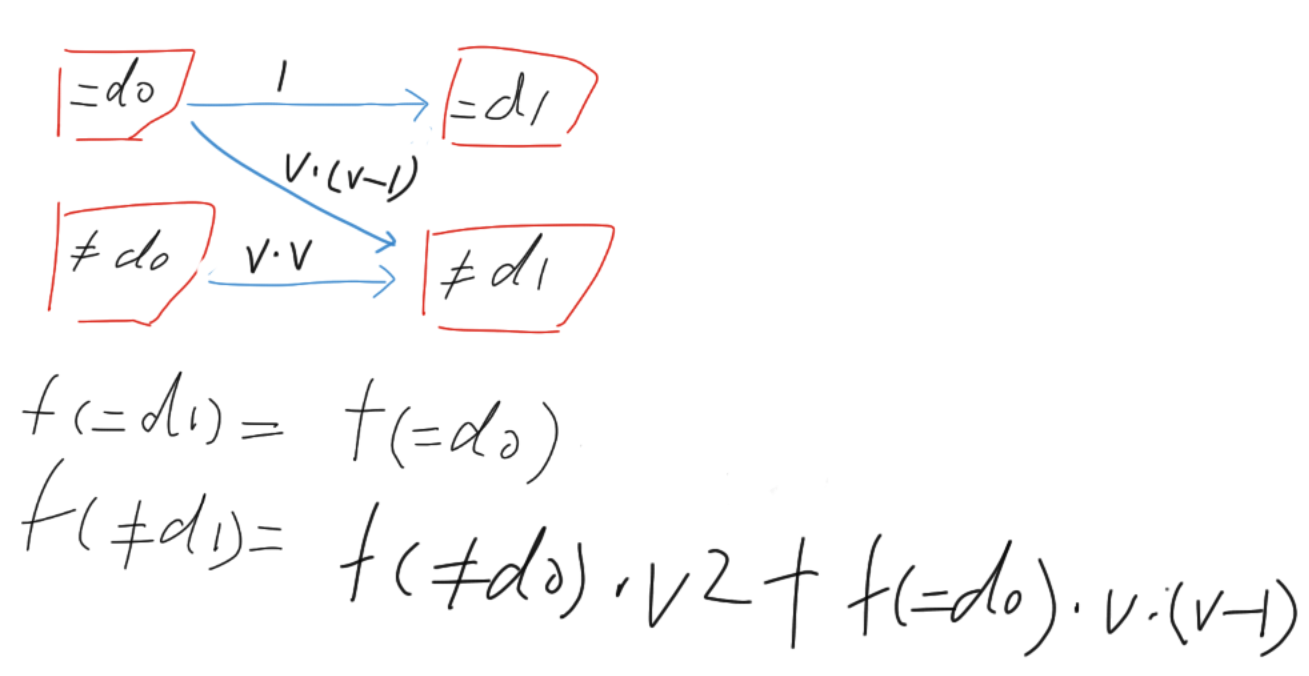
综合分析

上面我们分情况分析了不同位置的一元约束对二元约束方案数的影响。

可以看到，我们真正关心的状态只有两类：「当前被一元约束固定的二元关系数量」和「当前自由的二元关系数量」。
因此可以把状态压成 2 维，用矩阵乘法来统一描述转移，用矩阵快速幂来加速整体过程。

第一个矩阵对应「往后走一位且下一位没有一元约束」的转移，如下图：

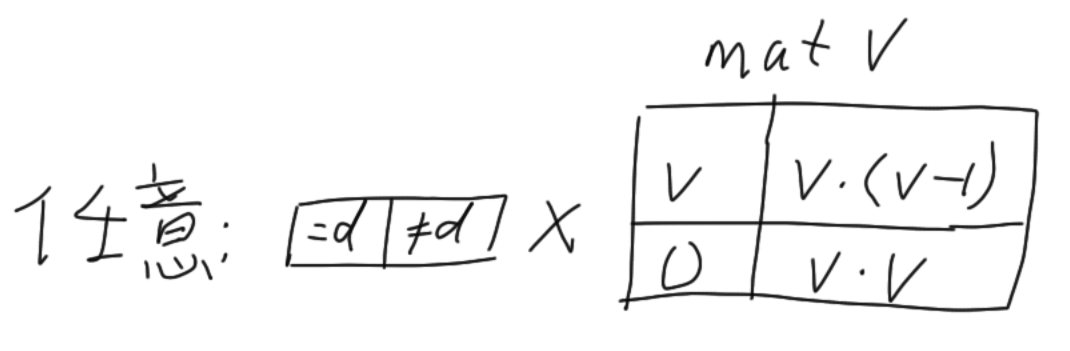
第二个矩阵对应「下一位有一元约束」的转移，如下图：

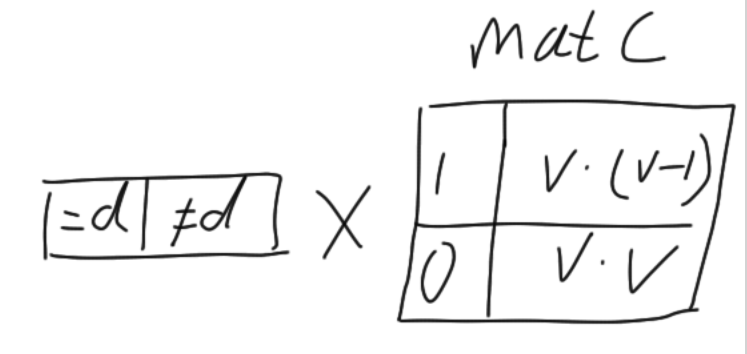
有了这两个转移矩阵，就可以使用矩阵快速幂来计算答案了。

第一步是先将一元约束按位置分组、去重：

map<ll, ll> H;
for (int i = 0; i < m; i++) {
  ll c, d;
  scanf("%lld%lld", &c, &d);
  if (H.count(c)) {
    if (H[c] != d) {
      noAns = 1; // 输入存在矛盾
    }
  } else {
    H[c] = d;
  }
}

之后，再根据相邻两次一元约束之间的距离，使用矩阵快速幂来快速计算中间这一段的贡献：

for (const auto& [p, _] : H) {
  const ll len = p - prePos;
  if (first == 1) {  // 第一个一元约束前面只有任意选择
    first = 0;
    Matrix mat(2);
    mat.a[0][0] = preVal1.x;
    Matrix tmp = mat * matV.pow(len);
    preVal1.x = (tmp.a[0][0] + tmp.a[0][1]) % mod;
  } else { // 有约束 -> 任意选择 -> 任意选择 -> 有约束
    Matrix mat(2);
    mat.a[0][0] = preVal1.x;
    Matrix tmp = mat * matV.pow(len - 1) * matC;
    preVal1.x = (tmp.a[0][0] + tmp.a[0][1]) % mod;
  }
  prePos = p;
  MyPrintf("  preVal1.x=%lld\n", preVal1.x);
}

const ll len = n - prePos;
if (len > 0) { // 处理最后一段
  Matrix mat(2);
  mat.a[0][0] = preVal1.x;
  Matrix tmp = mat * matV.pow(len);
  preVal1.x = (tmp.a[0][0] + tmp.a[0][1]) % mod;
}
printf("%lld\n", preVal1.x);

三、正难则反

其实，在第一段和最后一段，根本没有必要使用矩阵快速幂。

回顾前面的分析，当只有一个一元约束关系时，我们已经推导过：
答案就是 v^k * v^k，其中 k 为一元约束关系的位置。
也就是说，可以直接用普通快速幂来处理这一段。

所以，在整体流程中，第一段和最后一段可以都改成用普通快速幂，从而少做两次矩阵幂运算，速度会更快一些。

for (const auto& [p, _] : H) {
  const ll len = p - prePos;
  if (first == 1) {  // TYPE_0 -> TYPE_1
    first = 0;
    preVal1 = preVal1 * qpow(v, len * 2, mod);
  } else {  // TYPE_1 -> TYPE_V -> TYPE_1
    Matrix mat(2);
    mat.a[0][0] = preVal1.x;
    Matrix tmp = mat * matV.pow(len - 1) * matC;
    preVal1.x = (tmp.a[0][0] + tmp.a[0][1]) % mod;
  }
  prePos = p;
}
// 处理最后一段
const ll len = n - prePos;
if (len > 0) {
  preVal1 = preVal1 * qpow(v, len * 2, mod);
}
printf("%lld\n", preVal1.x);

而对于多个一元约束中间那一段，我们还可以换一个「正难则反」的思路来看问题。

我们的目标是求「合法的二元约束数量」，自然可以写成：

合法方案数 = 所有方案数 − 非法方案数。

这一段的「所有方案数」很好算：每条二元关系都有 v^2 种选法，整体是指数级的；
真正困难的是「非法方案数」，也就是那些一旦在前面选了某些二元关系，后面无论怎么选都无法满足一元约束的情况。

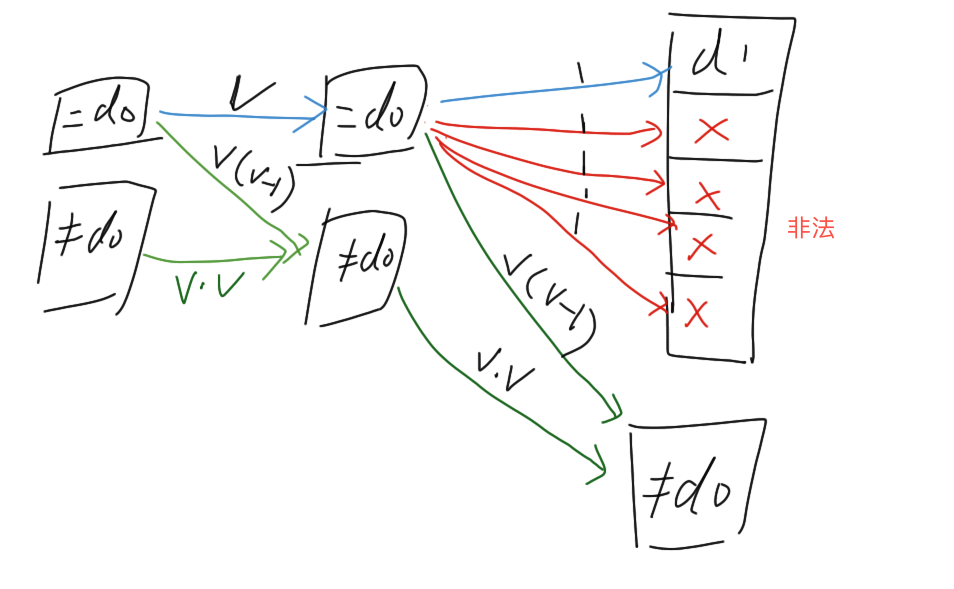
还是结合图来理解：
在没有一元约束时，上一个有约束的位置，有 v 个选择，到达 [1, v] 的任意一个位置，

因此可以产生 f(=d0) * v 个新的「有约束」位置。
最后在遇到下一次一元约束时，下一个位置只有一个取值是合法的，其余的 v-1 个取值都是非法的。

设两个一元约束之间相隔 k 个位置，那么总的非法方案数可以写成：

f(=d0) * v^(k-1) * (v-1)

代码上可以写成：

for (const auto& [p, _] : H) {
  const ll len = p - prePos;
  if (first == 1) {  // TYPE_0 -> TYPE_1
    first = 0;
    preVal1 = preVal1 * qpow(v, len * 2, mod);
  } else {  // TYPE_1 -> TYPE_V -> TYPE_1
    preVal1 = preVal1 * qpow(v, len * 2, mod)
            - preVal1 * qpow(v, len - 1, mod) * (v - 1);
  }
  prePos = p;
}
// 处理最后一段
const ll len = n - prePos;
if (len > 0) {
  preVal1 = preVal1 * qpow(v, len * 2, mod);
}

四、总结

这道题，我们实际上使用了两种思路来解决：

1. 正向建模 + 状态压缩成 2 维，用矩阵快速幂来做整体的加速；
2. 利用「正难则反」的思想，把复杂的中间段改成「总数减非法数」，并尽量用普通快速幂替代矩阵快速幂。

不管是正推，还是「正难则反」的反向思考，思维难度都不算低。
为了帮助理解，我画了不少图来说明状态和转移的含义。
希望这些图和推导过程能帮助你把这道题真正吃透。

《完》

-EOF-

本文公众号：天空的代码世界
个人微信号：tiankonguse
公众号 ID：tiankonguse-code